Министерство образования и науки Украины

Одесский национальный политехнический университет

Кафедра компьютеризированных систем управления

Лабораторная работа

на тему:

«Синтез разомкнутой оптимальной по быстродействию системы и ее исследование на модели»

по курсу

«Оптимальные и адаптивные системы»

Выполнила: ст. гр. АТ-001

Проверила: доц. Трофименко Т.Г.

Одесса 2006

Цель работы: построение замкнутой автоматической системы, оптимальной по быстродействию, и её исследование с помощью программного пакета Mathlab. Основная задача работы – определение оптимального алгоритма как функции измеряемых координат системы.

Теретические сведения.

Нахождение оптимальных по быстродействию алгоритмов управления различными объектами наиболее целесообразно осуществлять с применением принципа максимума.

Заданная С–часть системы описывается следующим дифференциальным уравнением:

(1.1)

На управляющее воздействие накладывается ограничение:

Критерий оптимальности имеет вид:

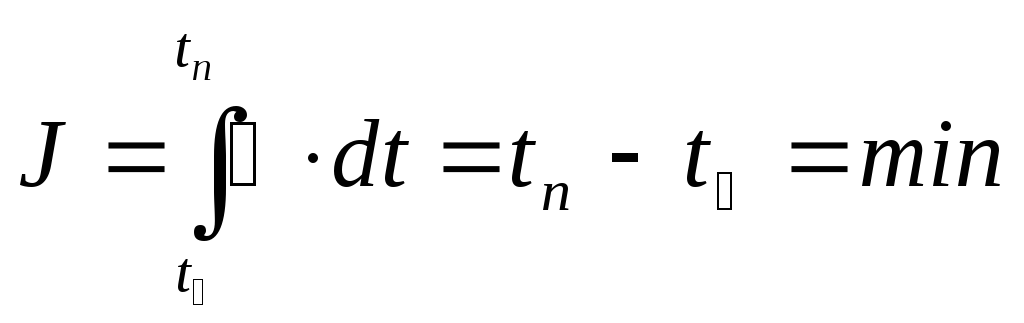(1.2)

Требуется найти такое управление u(t), при котором время перехода объекта из состояния y_o=0 в состояние y_n=2.2 было минимальным.

Перейдем в уравнении (3.1) от второго порядка к первому путем замены переменной:

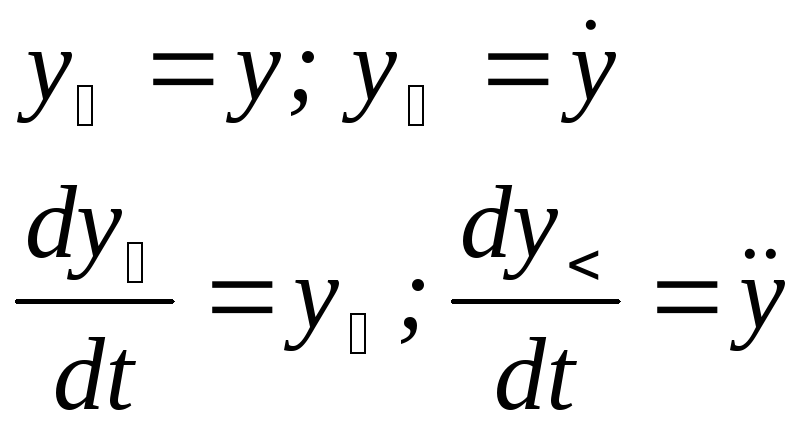
Т.к. критерий оптимальности (3.2) не содержит в явном виде управление, то отпадает необходимость введения новой дополнительной переменной. В результате получим следующую систему уравнений:

(1.3)

Составим функцию Понтрягина на основании системы (1.3):

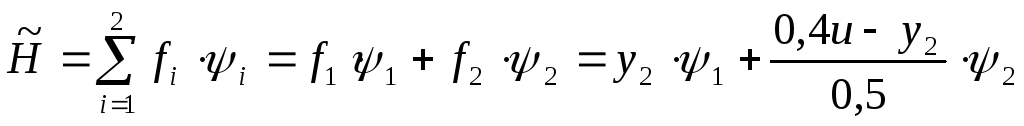(1.4)

В соответствии с принципом максимума управление будет оптимальным, если функция Н приобретает максимальное значение. Для определения такого управления необходимо из (1.4) определить частную производную функции H по u и приравнять нулю, т.е.

(1.5)

Для выполнения равенства (1.5) необходимо, чтобы . Это противоречит теореме Понтрягина. Поэтому, чтобы функция Н имела максимум, необходимо управляющее воздействие брать на границах допустимого значения, т.е. чтобы при и при . Отсюда оптимальный алгоритм управления приобретает вид:

(1.6)

Для определения функции составляется следующая система уравнений:

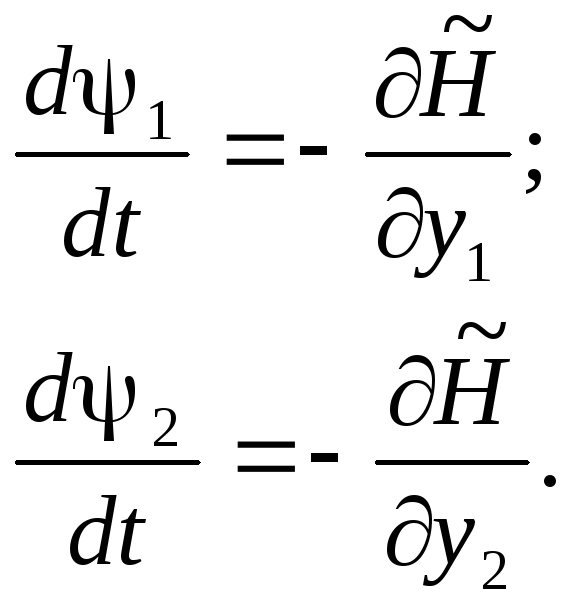(1.7)

Из (1.7) получим:

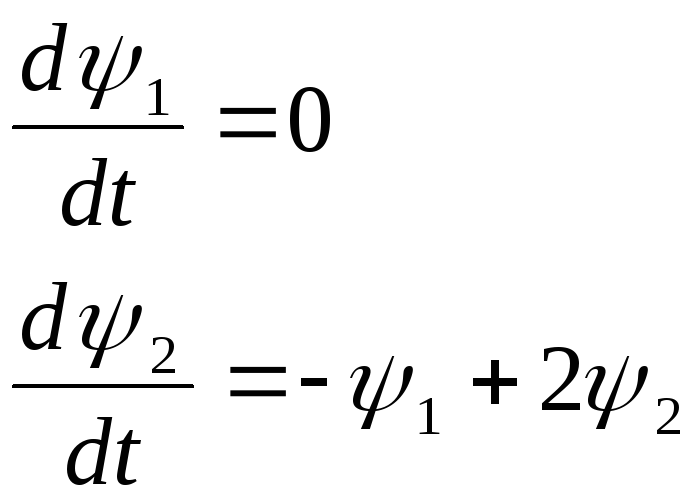(1.8)

Решением системы (1.8) является:

(1.9)

Подставляя (1.9) в (1.6), получаем оптимальный алгоритм управления:

(1.10)

В соответствии с (1.10) управляющее воздействие скачком принимает значения или . Это уравнение дает только качественную сторону изменения управляющего воздействия. Вместе с тем, при проектировании системы нужно знать и количественные характеристики, такие, как количество интервалов максимального значения управляющего воздействия и моменты переключения этого воздействия. Количество интервалов легко определить, пользуясь теоремой об n – интервалах, основное содержание которой состоит в следующем: если С-часть системы описывается линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами и корни его характеристического уравнения отрицательные или нулевые, то количество интервалов максимального значения управляющего воздействия должно быть n, а знаки на интервалах должны чередоваться (n-1) раз.

Таким образом, число интервалов определяем по корням характеристического уравнения С-части системы.

Дифференциальное уравнение, описывающее С-часть системы:

составим характеристическое уравнение:

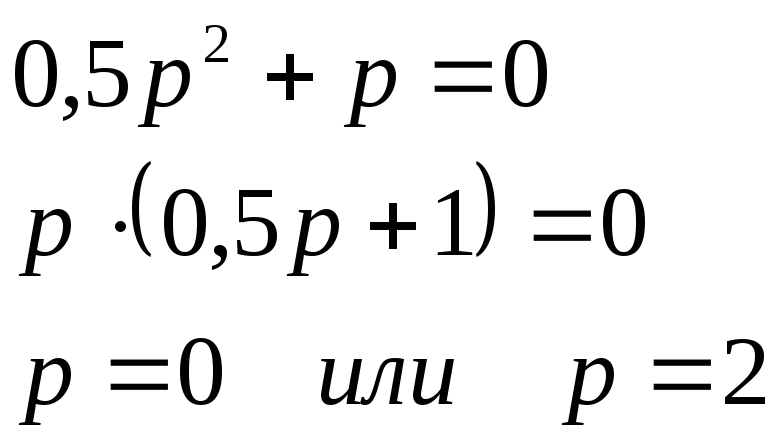(1.11)

Из (1.11) и теоремы об n – интервалах можно сделать вывод, что алгоритм управления будет состоять из двух интервалов управления .

Определим моменты переключения оптимального управляющего воздействия.

Решение (3.1) на втором интервале управления имеет вид:

(1.12)

где

- постоянные интегрирования на втором интервале

- корень характеристического уравнения

Используя условия на конец управления при получим систему уравнений:

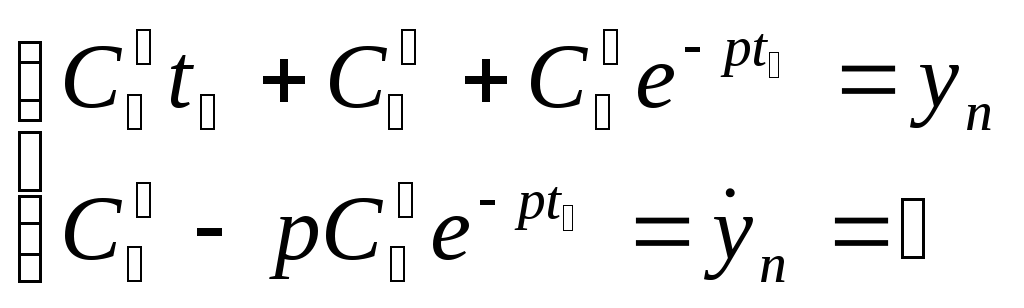(1.13)

Из системы (1.13) находим:

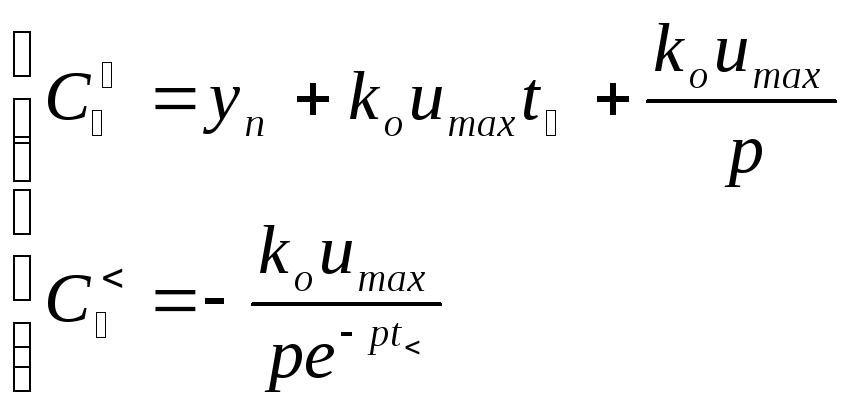(1.14)

Решение (1.1) на первом интервале управления:

(1.15)

где

- постоянные интегрирования на первом интервале

С учетом начальных условий при получим:

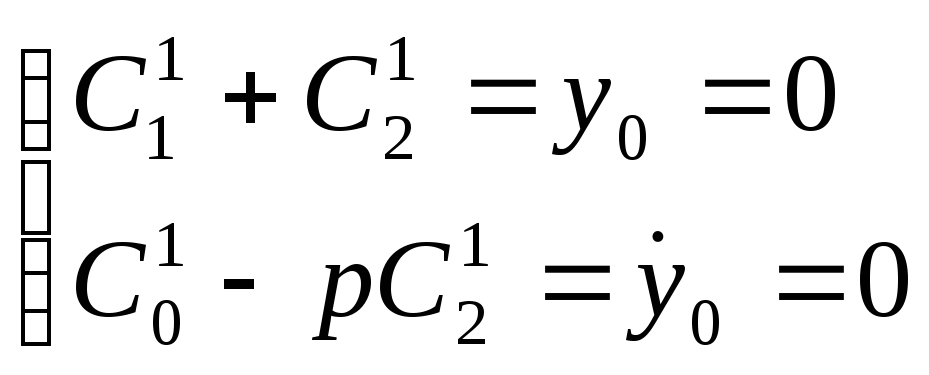(1.16)

Из системы (3.16) находим:

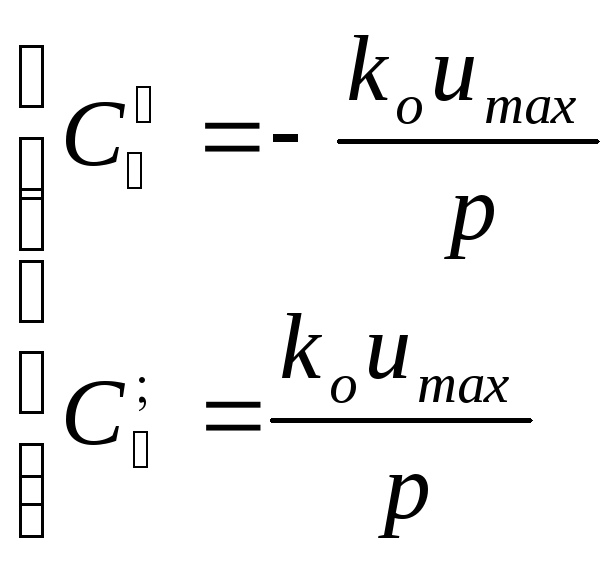(1.17)

Стыкуем решение в момент переключения t₁:

(3.18)

Подставим (1.14) и (1.17) в (1.18 ), получим уравнения для определения моментов переключения:

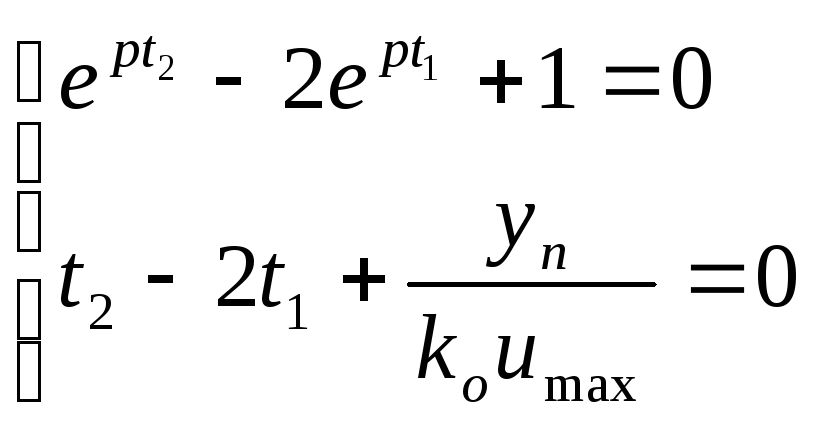(1.19)

Из второго уравнения системы (1.19) получим:

(1.20)

Подстановка (1.20) в первое уравнение системы (1.19) позволяет записать следующее:

(1.21)

Преобразуем (3.21) и умножив левую и правую части на получим:

(1.22)

Введем обозначение :

(1.23)

Подставим в (3.23) численные значения коэффициентов:

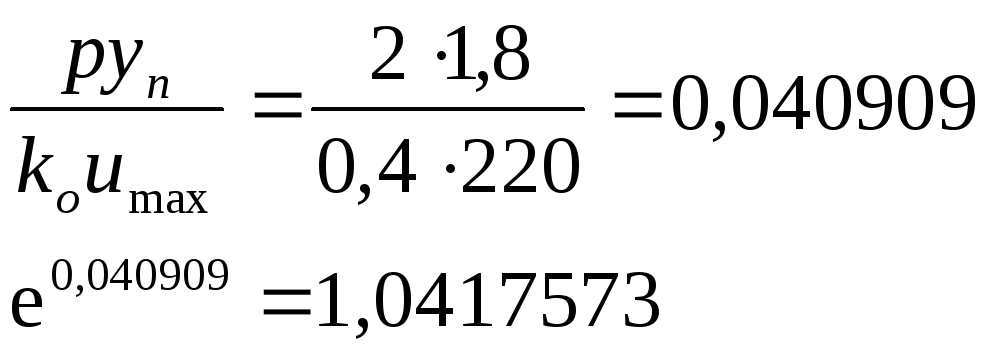
(1.24)

Решением полученного квадратного уравнения (1.24) является

Т.к. экспонента в положительной степени всегда больше единицы, то решением уравнения (1.24) является x₁. Поэтому, . Тогда:

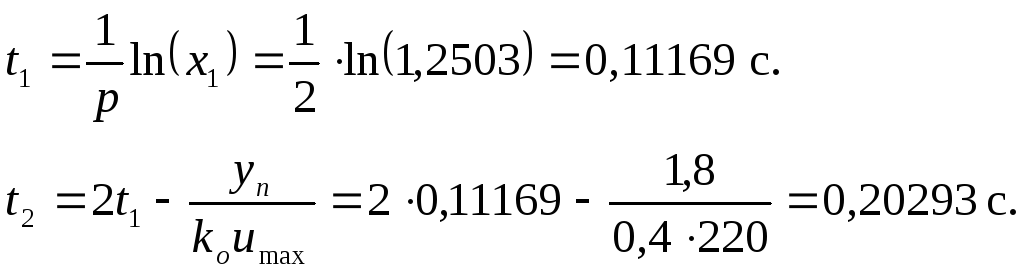
На рис. 1.1 приведено оптимальное управляющее воздействие, обеспечивающее перевод разомкнутой системы в заданное состояние за минимальное время.

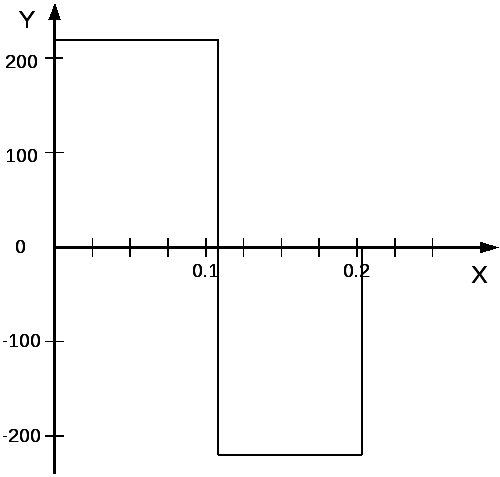
Рис. 1.1 График оптимального управляющего воздействия

Структурная схема оптимальной по быстродействию системы включает в себя все звенья системы и представляет математическую модель протекающих в ней процессов. Для составления структурной схемы были использованы уравнения динамики С – части, управляющего устройства и синтезированный алгоритм управления контура оптимизации. Взаимные связи между звеньями системы соответствуют полученной ранее функциональной схеме и обеспечивают требования оптимальности по быстродействию системы при отработке вводимого задающего воздействия.

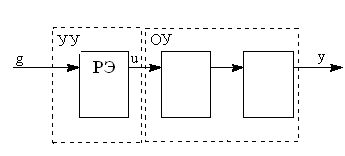
g(t) - задающее воздействие; y(t) - вектор состояния системы; u(t) - управляющее воздействие; УУ - управляющее устройство; ОУ - объект управления, РЭ - релейный элемент.

Расчет и построение переходного процесса проектируемой системы выполнялся для двух случаев. В первом случае рассматривалась оптимальная по быстродействию система с использованием принципа комбинированного управления при отключенном управляющем устройстве. Контур оптимизации при этом осуществляет непосредственное воздействие на управляемый объект, когда система является разомкнутой.

Во втором случае в рассматриваемой системе управления контур оптимизации отключен, система является замкнутой, но не оптимальной по быстродействию.

Решение уравнения (1.1) для первого интервала с учетом найденных постоянных интегрирования имеет вид:

(1.25)

С учетом численных значений параметров уравнение (1.24) записывается в следующем виде:

Результаты вычислений сведены в таблицу 1.

Таблица 1

t	0	0,012	0,024	0,036	0,048	0,052	0,064	0,086	0,098	0,112
Y(t)	0	0,013	0,0499	0,111	0,196	0,23	0,346	0,615	0,793	1,026

Решение уравнения (1.1) для второго интервала при t=t₁ и длительности имеет вид:

(1.26)

Определим постоянные интегрирования. С этой целью был рассмотрен условно момент времени t₁=0. Тогда из (1.26) следуют равенства:

(1.27)

Величина y_с соответствует моменту переключения. Значения в (1.27) находятся с помощью уравнений (1.14)

,

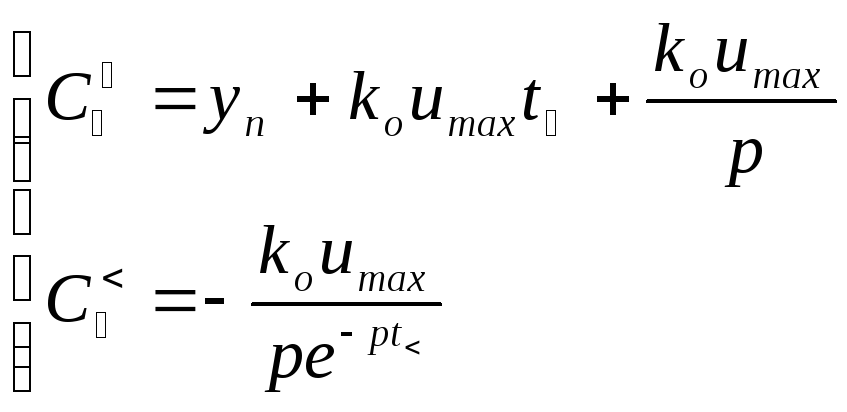в которых вместо t₂ используется t. В результате подстановки получим:

Подставляя полученные численные значения постоянных интегрирования в уравнение (1.26). Получим:

Таблица 2

t	0,015	0,03	0,045	0,06	0,075	0,091
Y(t)	1,259	1,453	1,6	1,71	1,77	1,8

Производная в момент времени t₂ :

Таким образом, условия в конце управления выполняются.

Используя данные таблиц 1 и 2, строится переходной процесс оптимальной по быстродействию системы (рис.1.2).

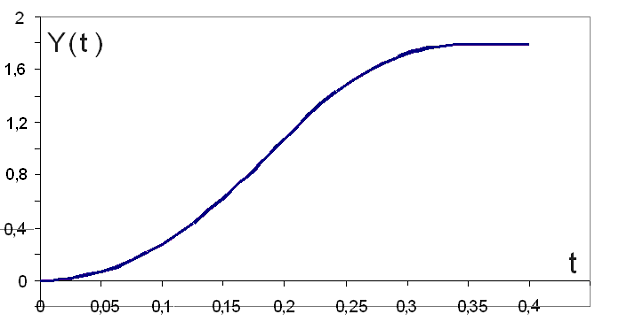
Рис. 1.2 Переходной процесс оптимальной по быстродействию системы

Построение переходной характеристики было проведено, используя приложение "Simulink" пакета "MatLab". Схема и результат моделирования представлены на рис. 1.3 и 1.4 соответственно.

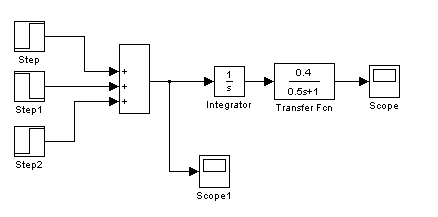
Рис. 1.3 Структурная схема системы оптимальной по быстродействию

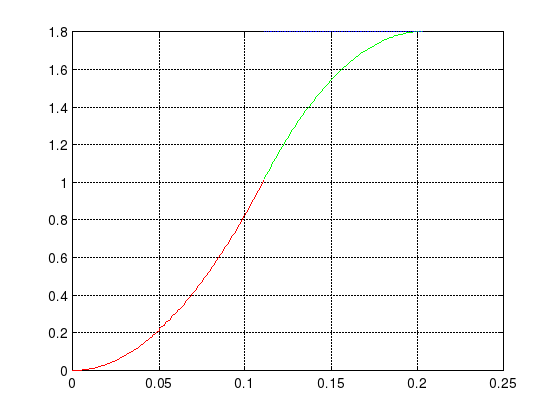
Рис. 1.4 Переходной процесс системы оптимальной по быстродействию.

Выводы: в ходе лабораторной работы была синтезирована структурная схема замкнутой системы, оптимальной по быстродействию, проведено исследование с помощью программного пакета Mathlab. А также были получены переходные процессы системы при значениях постоянной времени объекта и . Основная задача работы – определение оптимального алгоритма как функции измеряемых координат системы.

Литература

1. Воронов А. А. (ред.) Теория автоматического управления: Учеб. для вузов. Ч. П. – М.: Высш. шк., 1986.-504с.:ил.

2. Олейников В.П., Зотов Н.С., Пришвин А. М. Основы оптимального и экстремального управления. – М.: Высш. шк., 1969. – 296 с.

3. Пичугин Е.Д. Методические указания к лабораторной работе «Синтез оптимальной по быстродействию разомкнутой системы и ее исследование на модели», Одесса, ОНПУ, 2004.