5.1.3. Модификований метод Ейлера

На відміну від звичайного метода Ейлера в цьому методі використовується оцінка поведінки інтегральної кривої в наступних точках. Порядок побудови рішення в модифікованому методі Ейлера полягає в наступному.

Ч

Мал. 5.2. Модифікований метод Ейлера

ерез точку Р_i(X_i,Y_i) (мал. 5.2) проводиться дотична А₁ з тангенсом кута нахилу f(X_i,Y_i) до перетинання з ординатою в точці X=X_i + h/2 (по методу Ейлера (6)). Одержуїмо точку перетинання В з координатами (X_i+h/2, Y_i+h/2*Y_i'). Вираховуваем тангенс кута нахилу дотичної в цій точці: К_i=Y_i'+1/2=f(X_i+h/2, Y_i+h/2*Y_i'). Пряма з таким нахилом, яка проходить через точку В, позначена А₂. Далі, через точку Р_і(X_i,Y_i) проводимо пряму А_о, паралельну А₂. Перетинання прямой А_о з ординатою Х=Х_і+1 і дае шукану точку Р_і+1(X_i+1,Y_i+1).

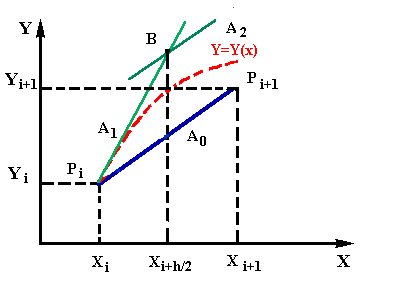
Рівняння прямої А_о можно записати:

Y_i+1=Y_i+K_i*(X_i+1-X_i)=Y_i+h*f(X_i+h/2,Y_i+h/2*Y_i') (5.9)

Формула (5.9) описуе модифікований метод Ейлера. Інтегрування за модифікованим методом Ейлера міститься у послідовному застосуванні формул (5.6) (при h=h/2) і (5.9) до рівняння (5.3), починаючи з I=1. Цей метод є більш точним (другого по рядку точності), ніж метод Ейлера (який маї перший порядок точності).

ПРИКЛАД.

Розв'язати модифікований метод Ейлера рівняння (5.8) з початковою умовою Y(0)=0, на відрізку [0; 4], крок h=1. Результати обчислень заносимо у табл. 5.2.(заповняючи її по строчкам)

Таблиця 2

Рішення рівняння (5.8) модифікованим методом Ейлера

i	Xi	Yi	Yi’= =f(Xi,Yi)	Xi +1/2 = =Xi+h/2	Yi+1/2= Yi+h/2*Yi’	Y’i+1/2= f(Xi +1/2, Yi+1/2)	h* Y’i+1/2
0	0	0	0.05	0.5	0.025	0.0486	0.0486
1	1	0.0486	0.0473	1.5	0.0722	0.0459	0.0459
2	2	0.0945	0.0446	2.5	0.117	0.0434	0.0434
3	3	0.138	0.0421	3.5	0.159	0.0410	0.0410
4	4	0.179

5.1.4. Метод Ейлера-Коши Мал. 5.3. Метод Ейлера- Коші

В цьому методі також використовується оцінка поведінки інтегральной кривой в послідуючих точках. Сутність метода Ейлера-Коши міститься в наступному (мал. 5.3).

За допомогою метода Ейлера (5.6) відшукуеться точка А(X_i+h,Y_i+h*Yi') - для чого в точці Д(X_i,Y_i) проводимо дотичну L₁ до перетинання з ординатою, яка всановлена в точці X_i+1=X_i+h.

В точці А знову обчислюеться тангенс кута нахилу дотичної і проводимо її. В точці А проводимо пряму , тангенс кута нахилу якої є середнє арифметичнем тангенсів кутів нахилу дотичних L₁ i L₂.

Через точку Д(Xi,Yi) проводимо пряму L, паралельну .Точка, в котрій пряма перетне ординату, востановлену в точці X_i+1=X_i+h, і буде шуканою точкою в(X_i+1,_Yi+1) . Формула метода Ейлера-Коши маї слідуючий вигляд:

Y_i+1=Y_i+h/2*[f(X_i,Y_i)+f(X_i+h,Y_i+h*Y_i')] (5.10)

Інтегрування по методу Ейлера-Коши міститься в послідовному застосуванні формул (5.6) i (5.10), починаючи з І=1. Спочатку, по (5.6) обчислюють приблизнї значення YP_i+1. Потім, визначивши YP_i+1, по (5.10) обчислюють шукане Y_i+1. Даний метод,т акож як і модифікований метод Ейлера, має другий порядок точності.

ПРИКЛАД.

Користуючись методом Ейлера-Коши, розв'язвти рівняння (5.8) з пер вісною умовою Y(0)=0, на відрізку [0; 4], крок h=1.

РІШЕННЯ: Результати обчислень приведенні в табл. 5.3.

Таблиця 5.3

Рішення рівняння (5.8) методом Ейлера-Коши

i	Xi	Yi	Yi’= =f(Xi,Yi)	Xi +1 = =Xi+h	YPi+1= Yi+h*Yi’	YP’i+1= f(Xi +1, YPi+1)	h*( Y’i+ +YP’i+1)/2
0	0	0	0.05	1	0.05	0.0473	0.0486
1	1	0.0486	0.0473	2	0.0959	0.0446	0.0460
2	2	0.0945	0.0446	3	0.139	0.0421	0.0434
3	3	0.138	0.0421	4	0.180	0.0398	0.0410
4	4	0.179

5.1.5. Методи Рунге-Кутта

Найбільш поширеними у практиці інтегрування звичайних диференційних рівнянь є методи Рунге-Кутта різноманітного порядку точності. Перевагою ціх методів є те, що при їх використовуванні не треба обчислювати похідні вищє першого порядку, а їх головний недолік - значний об'єм обчислень на кожному році.

До методів Рунге-Кутта відносяться метод Ейлера - метод Рунге-Кутта пер- шого порядку точності; модифікований метод Ейлера і метод Ейлера-Коши - метод Рунге-Кутта другого порядку.

Метод Рунге-Кутта четвертого порядку точності - один із найуживаніших методів інтегрування диференційних рівнянь. Взагалі його називають просто "методом Рунге-Кутта". Цей метод описуеться системою п'яти рівнянь:

Y_i+1=Y_i+h/6*(K1+2*K2+2*K3+K4) (5.11)

де K1=f(X_i,Y_i) (5.12)

K2=f(X_i+h/2,Y_i+h*K1/2) (5.13)

K3=f(X_i+h/2,Y_i+h*K2/2) (5.14)

K4=f(X_i+h,Y_i+h*K3) (5.15)

Інтегрування по методу Рунге-Кутта міститься в наступному. Для кожної і-ої точки (i=1,2,..,n-1) no (5.12) - (5.15) обчислюються значення К_j (j=1,2,3,4). Потім по (5.11) послідовно визначаються значення Y_i (i=1,2,..,n).