
- •Задание № 1 Выборка и сортировка таблиц
- •Задание № 2 Интерполирование полиномом Лагранжа
- •Рекомендации по выполнению задания
- •Пример расчета с помощью электронных таблиц ms excel
- •Расчетные формулы, используемые в ячейках
- •Задание № 3 Численное интегрирование
- •Численное интегрирование
- •Формула прямоугольников
- •Формула трапеций
- •Задание № 4 Решение систем линейных алгебраических уравнений (слау)
- •Исходные данные
- •Исходные данные
- •Исходные данные
- •Решение систем линейных алгебраических уравнений
- •Методы решения слау
- •Точные методы
- •Приближенные (итерационные) методы
- •Метод Гаусса (последовательного приближения неизвестных)
- •Итерационные методы решения слау
- •Метод Якоби (простой итерации)
- •Метод Гаусса - Зейделя
- •Рекомендации по использованию excel для решения слау № 1 и 3 с помощью обратной матрицы
- •Рекомендации по использованию excel для решения слау № 2 с помощью метода прогонки
Численное интегрирование
Г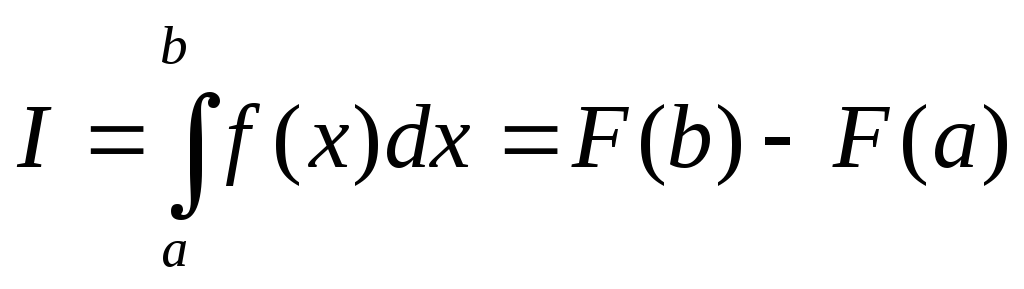 еометрическое
истолкование определенного интеграла:
интеграл численно равен площади,
покрываемой ординатами графика f(x),
т.е. площади криволинейной трапеции,
ограниченной осью абсцисс, отрезками
прямой x
= a,
x
= b
и графиком подынтегральной функции.
еометрическое
истолкование определенного интеграла:
интеграл численно равен площади,
покрываемой ординатами графика f(x),
т.е. площади криволинейной трапеции,
ограниченной осью абсцисс, отрезками
прямой x
= a,
x
= b
и графиком подынтегральной функции.
,
где F – первообразная.
Если первообразную найти сложно или невозможно, а также, если f(x) задана таблично или графиком, применяется численное интегрирование.
Формула прямоугольников
Промежуток интегрирования [a, b] делим точками x1, x2, ..., xn-1 на n равных частей; длина каждой
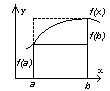 h
= ( b - a) / n .
h
= ( b - a) / n .
Т.е.x0 = a , xn = b, xi = a + i h, i = 0, 1, ..., n-1.
Пустьy 0 = f(x0), y i = f(xi), ... , y n = f(xn).
I ≈ (b - a) f(a) – формула левых прямоугольников
I ≈ (b - a) f(b ) - формула правых прямоугольников.
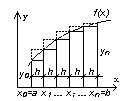
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
Выражения (3.1), (3.2) дают площади ступенчатых фигур.
Точность формул увеличивается с увеличением промежутков разбиения n.
Предельная
абсолютная погрешность
![]() (3.3)
(3.3)
Формула трапеций
П ромежуток
интегрирования[a,
b]
делим точками x1,
x2,
..., xn-1
на n
равных частей;
длина каждой
ромежуток
интегрирования[a,
b]
делим точками x1,
x2,
..., xn-1
на n
равных частей;
длина каждой
![]() (3.4)
(3.4)
Т.е. координаты узловых точек промежутков
x0 = a ,
xi = a + i h, i = 0,1, ..., n - 1 , (3.5)
xn = b
Соответственно, значения подынтегральной функции в этих точках
y 0 = f(x0),
y i = f(xi), ... , i = 0,1, ..., n - 1 , (3.6)
y n = f(xn).
![]() –формула
площади прямолинейной трапеций
–формула
площади прямолинейной трапеций
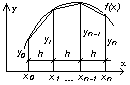
![]()
![]()
![]()
![]() (3.7)
(3.7)
Выражение (3.7) дает общую площадь трапеций.
Предельная
абсолютная погрешность
![]() (3.8)
(3.8)
Формула Симпсона (параболических трапеций)
Вершины трех соседних точек соединяются дугой квадратной параболы.
Ф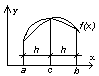 ормула
площади параболической трапеций
ормула
площади параболической трапеций
![]() ,
где
,
где
![]()
Промежуток интегрирования [a, b] делим точками x1, x2, ..., x2n-1 на 2n равных частей;
д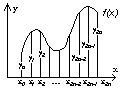 лина
каждой
лина
каждой![]() (3.9)
(3.9)
Т.е. координаты узловых точек промежутков
x0 = a ,
xi = a + i h, i = 0,1, ..., 2n - 1, (3.10)
x2n = b
Соответственно, значения подынтегральной функции в этих точках
y 0 = f (x0),
y i = f (xi), ... , i = 0,1, ..., 2n - 1 , (3.11)
y 2n = f (x2n).
![]()
![]()
![]() ,
(3.12)
,
(3.12)
 где
с =
где
с =
![]() .
.
Формула (3.12) дает точные результаты для полиномов не выше 3-ей степени.
Предельная
абсолютная погрешность
![]() (3.13)
(3.13)
Рекомендации по выполнению задания
Нахождение численного значения определенного интеграла (метод Симпсона)
В соответствии с номером варианта N выбирается интеграл, метод решения и число n.
Промежуток интегрирования разбивается на n или 2n равных промежутков по формулам (3.4) или (3.9) в зависимости от метода.
Определяются координаты узловых точек промежутков по формулам (3.5) или (3.10) и значения подынтегральной функции в этих точках по формулам (3.6) или (3.11).
Численное значение определенного интеграла вычисляется по формулам (3.7) или (3.12).
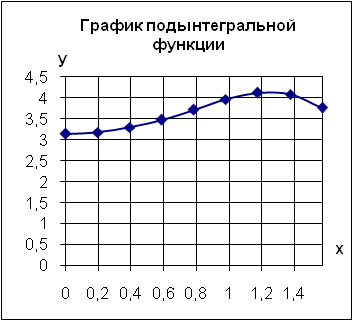
График подынтегральной функции строится на основании данных xi и y i.
Нахождение численного значения определенного интеграла методом Симпсона с помощью электронных таблиц EXCEL
|
|
А |
B |
C |
D |
E |
F |
G |
H |
i |
|
1 |
|
|
Численное интегрирование методом Симпсона | ||||||
|
2 |
|
|
|
|
Подынтегральная функция |
a |
b |
n |
h |
|
3 |
|
|
|
|
y = π + sin(x2 ) |
0 |
1,57 |
6 |
0,1308 |
|
4 |
|
i |
xi |
yi |
Численное значение интеграла |
|
|
|
|
|
5 |
|
0 |
0 |
3,140 |
|
|
|
| |
|
6 |
|
1 |
0,1308 |
3,157 |
|
|
|
| |
|
7 |
|
2 |
0,2617 |
3,208 |
|
|
|
| |
|
8 |
|
3 |
0,3925 |
3,293 |
5 |
|
|
|
|
|
9 |
|
4 |
0,5233 |
3,410 |
|
|
|
|
|
|
10 |
|
5 |
0,6542 |
3,555 |
|
|
|
|
|
|
11 |
|
6 |
0,7850 |
3,718 |
|
|
|
|
|
|
12 |
|
7 |
0,9158 |
3,884 |
|
|
|
|
|
|
13 |
|
8 |
1,0467 |
4,029 |
|
|
|
|
|
|
14 |
|
9 |
1,1775 |
4,123 |
|
|
|
|
|
|
15 |
|
10 |
1,3083 |
4,130 |
|
|
|
|
|
|
16 |
|
11 |
1,4392 |
4,017 |
|
|
|
|
|
|
17 |
|
12 |
1,5700 |
3,766 |
|
|
|
|
|
Пояснения:
В ячейки F3, G3, H3 введены исходные данные a, b и n, в ячейку i3 - значение h , вычисленное по формуле (3.9), т.е. = (G3 – F3) / (2*H3).
В диапазоне С5 : С17 вычислены значения xi по формуле (3.10), т.е. в ячейку С5 введена формула = $F$3 + $i$3 * B5, затем с помощью приема автозаполнения эта формула распространена на остальные ячейки диапазона.
В диапазоне D5 : D17 вычислены значения подынтегральной функции yi по формуле (3.11), т.е. в ячейку D 5 введена формула = Пи( ) + SIN (С5^2), затем эта формула распространена на остальные ячейки диапазона.
В ячейке Е8 записана формула (3.12) определения численного значения определенного интеграла по методу Симпсона
=i3/3*(D5+D17+4*(D6+ D8+D10+D12+D14+D16)+2*(D7+D9+D11+D13+ D15)).
На основании смежного диапазона С5 : D17 построена диаграмма категории «Точечная», на которой представлен график подынтегральной функции y = f(х) .
Примечание: расчет методом трапеций выполняется аналогично, по соответствующим формулам

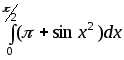
 ,7689
,7689