ЭД / Новая папка / ЛК 3 ТЭД_и_РРВ

ЭД и РРВ (ЛК 3)

Граничные условия для векторов электромагнитного поля. Метод комплексных амплитуд.

Уравнения Максвелла для комплексных векторов электромагнитного поля.

Комплексная диэлектрическая и магнитная проницаемости среды.

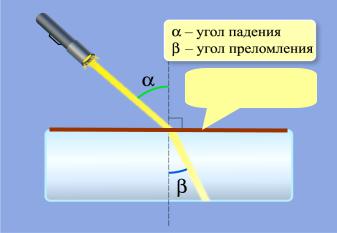
ЭД и РРВ (ЛК 3)

Граничные условия для векторов электромагнитного поля

Пусть достаточно гладкая поверхность S разделяет две среды, в каждой из которых параметры либо постоянны, либо меняются медленно от точки к точке. Тогда в малой окрестности любой точки на поверхности S можно счи- тать границу плоской, а параметры сред – неизменными. Таким образом, из рассмотрения исключаются точки, лежащие вблизи изломов и резких изгибов

границы или в области быстрого изменения параметров хотя бы одной из сред.

Рассмотрим некоторую поверхность S, разделяющую две среды с параметра-

ми εa1,μa1, σ1 и εa2 ,μa2 , σ2

В каждой точке поверхности S можно провести касательную плоскость P и три единичных вектора: n0 – нормаль, направленная из второй среды в пер-

вую; N0 , rτ0 – векторы, лежащие в плоскости Р (касательные к границе разде-

ЭД и РРВ (ЛК 3)

Граничные условия для векторов электромагнитного поля

Из этих соотношений следует, что касательные составляющие Е1τ и Е2τ векто-

ра E и нормальные составляющие В1n и В2n вектора B при переходе через границу раздела сред всегда непрерывны. Касательные составляющие Н1τ и

Н2τ вектора H и нормальные составляющие D1n и D2n вектора D непрерывны только в том случае, если на границе раздела сред отсутствуют соответствен- но ток с поверхностной плотностью js и заряды с поверхностной плотностью

E2 E2n

E2τ

ЭД и РРВ (ЛК 3)

Граничные условия для векторов электромагнитного поля

Пусть одна из сред, например, вторая является идеальным проводни- ком. Из уравнений Максвелла следует, что в идеальном проводнике (σ = ∞) электромагнитное поле отсутствует. Учитывая этот факт по- лучаем, что на поверхности идеального проводника граничные усло- вия имеют следующий вид:

Из последних соотношений следует, что силовые линии вектора E всегда перпендикулярны, а силовые линии вектора B всегда каса- тельные к поверхности идеального проводника.

Используя граничные условия и материальные уравнения,

можно записать граничные условия для касательных составляющих векторов D и B и нормальных составляющих векторов E и H .

ЭД и РРВ (ЛК 3)

Метод комплексных амплитуд

Все реальные электромагнитные процессы можно представить в виде суммы дискретных гармонических колебаний или непрерывного спектра этих коле- баний. Поэтому изучают поля при гармонических воздействиях. Такие поля называют монохроматическими (одноцветными).

Рассмотрим некоторый гармонический процесс, который характеризуется следующей функцией Ψ(t)

Ψ(t) = Ψm cos(ωt + ϕ),

где ω = 2π/f – угловая частота; ϕ – начальная фаза; Ψm – амплитуда гармони- ческого процесса.

В соответствии с методом комплексных амплитуд вместо действительной функции Ψ(t), меняющейся во времени по гармоническому закону, рассмат- ривается комплексная функция Ψ& (t) следующего вида

Ψ& (t)= Ψmei(ωt+ϕ) = Ψmeiϕeiωt = Ψ& meiωt ,

ЭД и РРВ (ЛК 3)

Метод комплексных амплитуд

где i = 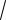−1 – мнимая единица; Ψ& m – комплексная амплитуда функции Ψ(t). Если комплексная амплитуда известна, то

Ψ(t) = Re[Ψ& meiωt ]= ReΨ& .

Вычислим производную по времени от функции Ψ& (t)

dΨ& (t) = iωΨ& meiωt = iωΨ& (t). dt

Из последней формулы видно, что операция дифференцирования над ком- плексной функцией Ψ& (t) заменяется умножением на iω.

В комплексной амплитуде Ψ& m заключена вся информация об амплитуде и на-

чальной фазе действительной функции Ψ(t). Если к тому же известна частота гармонического процесса ω, то можно определить действительную функцию

Ψ(t).

ЭД и РРВ (ЛК 3)

Метод комплексных амплитуд

Изложенное выше остается справедливым и для векторного случая.

Рассмотрим гармонический процесс, который характеризуется векторной

гармонической функцией следующего вида

( ) = r ω + ϕ + r ω + ϕ + v ω + ϕ ,

A t x0 Axm cos( t x ) y0 Aym cos( t y ) z0 Azm cos( t z )

где ϕx, ϕy ϕz – начальные фазы, а Axm, Aym, Axm – амплитуды соответствующих

плексной амплитудой векторной гармонической функции, exp(iϕ) ≡ eiϕ .

Для векторной гармонической функции также имеют место следующие соот- ношения:

ЭД и РРВ (ЛК 3)

Метод комплексных амплитуд

Отметим еще раз, что решение задач электродинамики для монохроматических полей значительно упрощается при использовании комплексных векторов.