Лекция_6а математическое описание

АВТОМАТИЧЕСКИХ СИСТЕМ (ПРОДОЛЖЕНИЕ)

СОДЕРЖАНИЕ

5.8.2 Свойства преобразования Лапласа

5.8.3 Решение дифференциальных уравнений

5.8.4 Разбиение на простейшие дроби

5.9 Передаточная функция

5.10 Тренировочные задания

5.11 Тест

5.8.2 Свойствапреобразования Лапласа

При использованиипреобразования Лапласа необходимо знать и применятьегосвойства, некоторыеиз них формулируютсяследующим образом.

1 Теорема линейности: для любыхдействительныхиликомплексныхпостоянных А и В линейнойкомбинацииоригиналовсоответствуеттакая же комбинация зображений

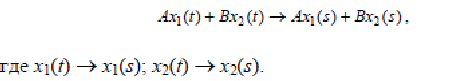(18)

2 Теорема подобия: умножениеаргументаоригинала на любоепостоянноеположительное число λприводит к делениюаргументаизображения x(s) на то же число λ :

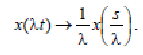(19)

3 Теорема затухания: умножениеоригинала на функцию e at , где а – любоедействительноеиликомплексное число, влечет за собой''смещение" независимойпеременной s:

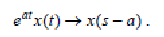(20)

4 Теорема запаздывания: для любого постоянного τ > 0

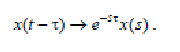(21)

5 Теорема дифференцирования по параметру: если при любомзначении r оригиналу x(t, r) соответствуетизображение х(s, r), то

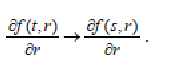(22)

6 Теорема дифференцированияоригинала: если x(t) → x(s), то

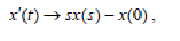(23)

т.е. дифференцированиеоригиналасводится к умножению на s егоизображения и вычитанию х(0).В частности, если х(0) = 0, то x'(t) → sх(s). Применяя теорему необходимоеколичество раз, получают

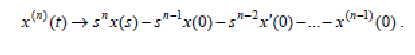(24)

Если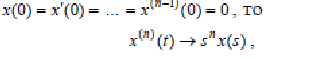(25)

т.е. при нулевыхначальныхзначениях n-кратноедифференцированиеоригиналасводится к умноженнюнаегоизображения.

7 Теорема интегрированияоригинала: интегрированиеоригинала в пределах от 0 до t приводит кделениюизображения на s:

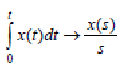(26)

8 Теорема дифференцированияизображения: дифференцированиеизображениясводится к умножениюоригинала на (-t)

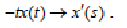(27)

9 Теорема интегрированияизображения: интегрированиюизображения в пределах от s до ∞ соответствуетделениеоригинала на t, т.е. еслиинтегралсходится то

(28)

10 Теорема умноженияизображения: если x(t) → x(s), y(t) → y(s), то сверткефункций

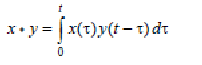(29)

соответствуетпроизведениеизображений

(30)

11 Теорема умноженияоригиналов: произведениюоригиналовсоответствуетсверткаизображений

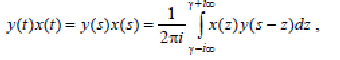(31)

где γ = Re z.

12 Теорема о конечном и начальномзначенияхфункции:

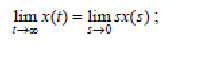(32)

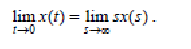(33)

5.8.3 Решениедифференциальныхуравнений

Одним изважнейшихпримененийоперационногоисчисления – преобразования Лапласа – являетсярешениелинейныхдифференциальныхуравнений с постояннымикоэффициентами, которымикак раз иописываютсярассматриваемыесистемыавтоматическогоуправления.Решениедифференциальногоуравнения в этомслучаескладываетсяизследующихэтапов:

1) преобразованиеуравнения по Лапласу;

2) отысканиерешения в области комплексного переменного s;

3) переход в область действительногопеременногопутемобратногопреобразования Лапласа.

Пример 5.2

Преобразуемданноеуравнение по Лапласу:

откуда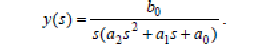Пусть полином

имеет корни тогда, какбудет показано ниже, можнозаписать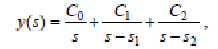

где C₀,C₁,C₂– некоторыекоэффициенты, определяемые методом неопределенныхкоэффициентов:

Пользуясьтаблицамиобратногопреобразования Лапласа, находим

Полученноевыражение y(t) являетсярешениемлинейногообыкновенногодифференциальногоуравнениявторогопорядка при входномсигнале x(t) = 1(t), т.е. ничеминым, какпереходнойфункциейдля линейногообъектавторогопорядка.