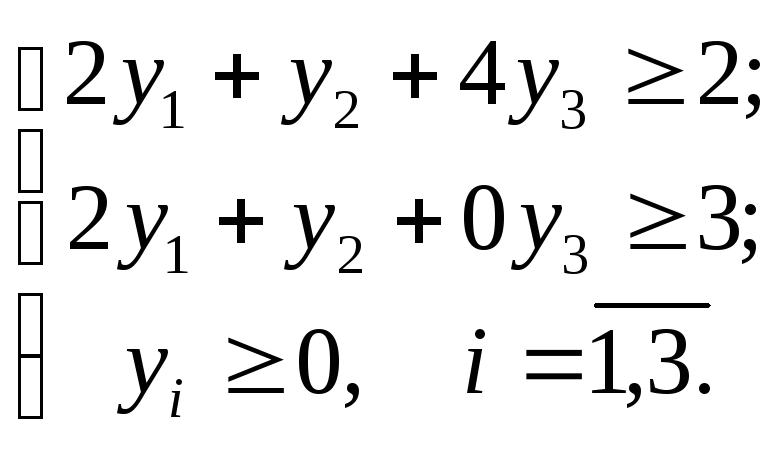2 Завдання.

Є постачальники з відповідною пропозицією: ,,і споживачі з відповідним попитом:,,,. Вартість перевезень від i-того постачальника до j-тому споживачеві задана матрицею витрат.

Необхідно:

1. Перевірити, чи є транспортна задача відкритою або закритою.

2. Скласти математичну модель, при якій вартість перевезення буде мінімальною.

3. За допомогою методу мінімальних витрат знайти початкове опорне рішення.

4. Оптимальний план транспортної задачі знайти за допомогою методу потенціалів.

5. Дати економічну інтерпретацію знайденого рішення.

Приклад розв’язання завдання: варіант № 0

1 Завдання.

Відомо, що для виготовлення двох видів продукції іпідприємству необхідно три види сировини: Запаси сировини; число одиниць сировини, затрачуваних на виготовлення одиниці продукції і прибуток від реалізації кожного виду продукції задані в табл. 1.

Табл.1

Вид сировини	Запас сировини	Витрати сировини на одиницю продукції, ум. од., за видами:
		P1	P2
S1	12	2	2
S2	8	1	2
S3	16	4	0
Прибуток		2	3

Потрібно:

1. Скласти математичну модель задачі планування виробництва продукції, при якій прибуток буде максимальним (скласти задачу лінійного програмування (ЗЛП) у стандартній формі з обмеженнями-нерівностями).

2. Вирішити ЗЛП графічним методом.

3. Дати економічну інтерпретацію знайденого рішення. Записати скільки одиниць кожного виду продукції необхідно виготовити підприємству 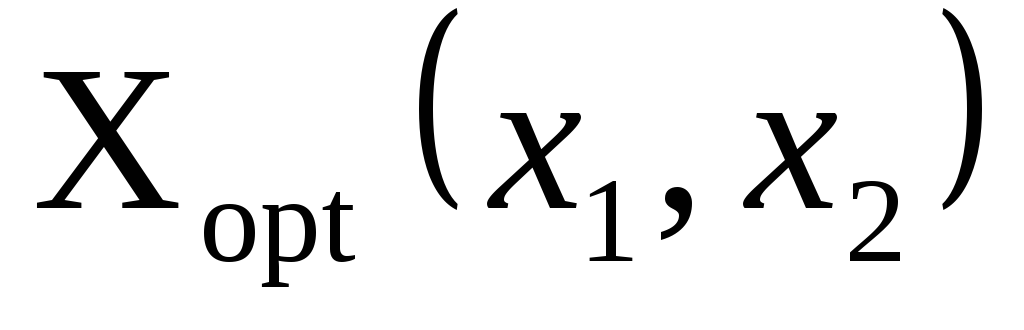для того, щоб дістати максимальний прибуток.

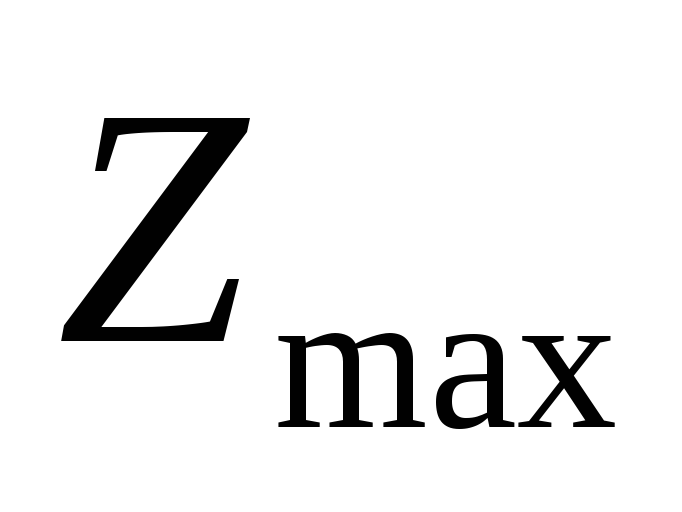4. Привести ЗЛП до канонічної форми з обмеженнями-рівностями. Заповнити симплекс-таблицю (табл.2.). Розв’язати ЗЛП симплексним методом.

Табл.2

ci		c0	c1=	c2=	c3=	c4=	c5=		Опорне рішення:
	Xбаз	B	x1	x2	x3	x4	x5
									z0 ; (x1,x2,x3,x4,x5)
		z0=	Δ1=	Δ2=	Δ3=	Δ4=	Δ5=

5.Побудувати двоїсту задачу.

Розв’язання :

1. Нехай X₁ одиниць продукції виду P₁, а X₂ одиниць продукції виду P₂. Тоді математична модель задачі планування виробництва продукції має вигляд:

z_max = 2x₁ + 3x₂

2х₁ + 2х₂ 12,

х₁ + 2х₂ 8,

4х₁ + 0х₂ 16,

х₁, х₂ 0.

2.Розв’яжемо ЗЛП графічним методом.

12 3 4 5 6 7 8 9 10 11 12 X₁

8

7

6

5

4

3

2

1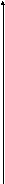

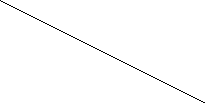
(2;3)

2х₁ + 2х₂ = 12

х₁ + 2х₂ = 8

4х₁ + 0х₂ = 16

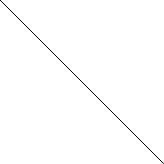
Вектор-цілі (2;3)

z_max = z_c

Визначимо координати точки С :

(С) 2х₁ + 2х₂ = 12

4х₁ = 16

х₁ = 4

х₂ = 2

Z_max = 2  4 + 3  2 = 14.

3. Підприємству необхідно виготовити чотири одиниці продукції виду Р₁ і дві одиниці продукції виду Р₂, щоб отримати максимальний прибуток 14 грошових одиниць.

4.Приведемо ЗЛП до канонічної форми з обмеженнями-рівностями.

Z_max = 2x₁ + 3x₂

2x₁ + 2x₂ + x₃ = 12,

x₁ + 2x₂ + x₄ = 8,

4x₁ + 0x₂ + x₅ =16,

x_i 0, i =.

Заповнимо симплекс-таблицю (табл.2.), та розв’яжемо ЗЛП симплексним методом:

Табл.2

ci		C0=0	c1=2	c2=3	c3=0	c4=0	c5=0		Опорне рішення:
	Xбаз	B	x1	x2	X3	x4	x5
0 0 0	X3 X4 X5	12 8 16	2 1 4	2 2 0	1 0 0	0 1 0	0 0 1		z0=0 =(0,0,12,8,16)
		z0=0	Δ1=-2	Δ2=-3	Δ3=0	Δ4=0	Δ5=0
0 3 0	X3 X4 X5	4 4 16	1 1/2 4	0 1 0	1 0 0	-1 1/2 0	0 0 1		z1=12 =(0,4,4,0,16)
		z1=12	Δ1=-1/2	Δ2=0	Δ3=0	Δ4=3/2	Δ5=0
2 3 0	X3 X4 X5	4 2 0	1 0 0	0 1 0	1 -1/2 -1/4	-1 1 4	0 0 1		Z2=14 =(4,2,0,0,0)
		Z2=14	Δ1=0	Δ2=0	Δ3=1/2	Δ4=1	Δ5=0

Так як в оціночній строчці є від’ємні елементи, тому дане опорне рішення не є оптимальним.

5. Побудувати двоїсту задачу.
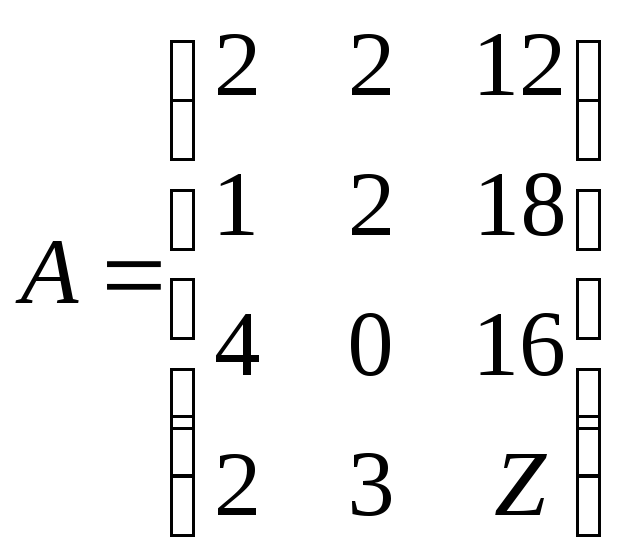