Геометрия / Лекция 3

1.6. Размерность линейного пространства

Эта важнейшая характеристика линейного пространства связана со свойствами систем векторов в этом пространстве.

Определение 1.5. Максимальное количество линейно независимых векторов в данном линейном пространстве называют размерностью линейного пространства.

Если размерность линейного пространства С равна n, т.е. существует линейно независимая система из п векторов, а любая система векторов, содержащая вектор или более, линейно зависима, то говорят, что это линейное пространство п-мерно. Размерность такого линейного пространства обозначают

Существуют линейные пространства, в которых можно выбрать линейно независимую систему, содержащую сколь угодно большое количество векторов. Такие линейные пространства называют бесконечномерными. В отличие от них, n-мерные линейные пространства называют конечномерными. Мы будем рассматривать конечномерные линейные пространства.

Пример 1.12. Линейное пространство функций, непрерывных на отрезке [0,1] (см. 1.1), является бесконечномерным, так как для любого натурального п система многочленов , являющихся элементами этого линейного пространства, линейно независима. В самом деле, линейная комбинация этих многочленов, отвечающая набору коэффициентов 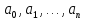, есть многочлен

,

который является нулевым (т.е. равен постоянной функции 0), только если все его коэффициенты (они же коэффициенты линейной комбинации) равны нулю.

Оказывается, что размерность линейного пространства тесно связана с количеством векторов, которое может иметь базис линейного пространства.

Теорема 1.4. Если линейное пространство 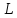n-мерно, то любая линейно независимая система из п векторов является его базисом.

Пусть система векторов 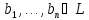линейно независима. Тогда для любого вектора 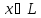система векторов линейно зависима, так как она содержит вектор, т.е. количество большее, чем размерность линейного пространства. Это значит, что существуют такие коэффициенты , одновременно не равные нулю, что

(1.6)

Заметим, что , так как в противном случае равенство (1.6) сводится к равенству

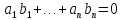
причем среди коэффициентов есть хотя бы один ненулевой (так как ). Но это означало бы, что система векторов линейно зависима. Учитывая, что , из (1.6) находим

Так как вектор х был выбран произвольно, заключаем, что любой вектор в линейном пространстве можно представить в виде линейной комбинации системы векторов Поэтому эта система векторов, по предположению линейно независимая, является базисом в .

Теорема 1.5. Если в линейном пространстве существует базис из п векторов, то .

(Без доказательства)

Из теорем 1.4 и 1.5 следует, что в каждом линейном пространстве любые два базиса содержат одно и то же количество векторов, и это количество равно размерности линейного пространства.

Пример 1.13. В линейном арифметическом пространстве стандартный базис (1.5) состоит из п векторов, поэтому , что и отражено в обозначении этого линейного пространства.

Пример 1.14. Рассмотрим однородную СЛАУ

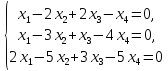
множество решений которой образует линейное пространство. Найдем размерность этого линейного пространства и какой-либо базис в нем.

Решим эту систему, определив ее фундаментальную систему решений. Для этого запишем матрицу системы и при помощи элементарных преобразований строк приведем ее к треугольному виду:

Из полученного находим, что в качестве свободных неизвестных можно взять и 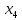, а в качестве базисных неизвестных - и .Преобразованная система имеет вид

Полагая 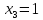и , находим и , а при и имеем и . Записав найденные решения в виде столбцов, получим фундаментальную систему решений:

Согласно теории систем линейных алгебраических уравнений, эти два решения линейно независимы, а любое другое решение СЛАУ представляется в виде их линейной комбинации. Другими словами, столбцы и 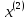образуют базис в линейном пространстве решений рассматриваемой однородной СЛАУ. Размерность этого линейного пространства равна двум - количеству векторов в базисе.

1.7. Преобразование координат вектора при замене базиса

В линейном пространстве все базисы равноправны. Тот или иной базис выбирают исходя из конкретных обстоятельств, а может быть, и вообще произвольно. Иногда удобно использовать для представления элементов линейного пространства несколько базисов, но тогда естественным образом возникает задача преобразования координат векторов, которое связано с изменением базиса.

Пусть в n-мерном линейном пространстве 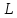заданы два базиса: стары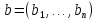й и новый . Любой вектор можно разложить по базису b. В частности, каждый вектор из базиса с может быть представлен в виде линейной комбинации векторов базиса b:

Запишем эти представления в матричной форме:

или , где

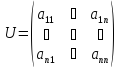(1.7)

Определение 1.6. Матрицу (1.7) называют матрицей перехода от старого базиса b к новому базису с.

Согласно данному определению, i-й столбец матрицы перехода есть столбец координат i-го вектора нового базиса в старом. Поэтому говорят, что матрица перехода состоит из координат векторов нового базиса в старом, записанных по столбцам.

Обсудим некоторые свойства матрицы перехода.

1°. Матрица перехода невырождена и всегда имеет обратную.

Действительно, столбцы матрицы перехода - это столбцы координат векторов нового базиса в старом. Следовательно, они, как и векторы базиса, линейно независимы. Значит, матрица U невырожденная и имеет обратную матрицу .

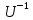2°. Если в n-мерном линейном пространстве задан базис b, то для любой невырожденной квадратной матрицы U порядка п существует такой базис с в этом линейном пространстве, что U будет матрицей перехода от базиса b к базису с.

Из невырожденности матрицы U следует, что ее ранг равен n, и поэтому ее столбцы, будучи базисными, линейно независимы. Эти столбцы являются столбцами координат векторов системы . Линейная независимость столбцов матрицы U равносильна линейной независимости системы векторов с. Так как система с содержит п векторов, причем линейное пространство п-мерно, то, согласно теореме 1.4, эта система является базисом.

Пример 1.15. Пусть - базис линейного пространства. Тогда система векторов тоже является базисом в этом линейном пространстве. Это следует из того, что

,

где диагональная матрица невырождена.

3°. Если U — матрица перехода от старого базиса b к новому базису с линейного пространства, то 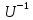— матрица перехода от базиса с к базису b.

Матрица невырождена, и поэтому из равенства следует, что 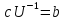. Последнее равенство означает, что столбцы матрицы 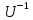являются столбцами координат векторов базиса b относительно базиса с, т.е., согласно определению 1.6, — это матрица перехода от базиса с к базису b.

4°. Если в линейном пространстве заданы базисы b, с и d, причем U — матрица перехода от базиса b к базису с, а V — матрица перехода от базиса с к базису d то произведение этих матриц — матрица перехода от базиса b к базису d.

Согласно определению 1.6 матрицы перехода, имеем равенства

,

откуда

,

т.е. — матрица перехода от базиса b к базису d.

Рассмотрим теперь, как преобразуются координаты произвольного вектора в линейном пространстве при переходе от старого базиса к новому. Выберем произвольный вектор и разложим его в старом базисе:

(1.8)

Разложение того же вектора в новом базисе имеет вид.

(1.8)

Найдем связь между старыми координатами х вектора х и новыми его координатами . Из соотношений (1.8), (1.9) следует, что . Учитывая, что , получаем 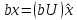или . Последнее равенство можно рассматривать как запись двух разложений одного и того же вектора х в данном базисе b. Разложениям соответствуют столбцы координат х и 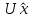которые, согласно теореме 1.2 о единственности разложения вектора по базису, должны быть равны:

или .

Итак, чтобы получить координаты вектора в старом базисе, необходимо столбец координат этого вектора в новом базисе умножить слева на матрицу перехода из старого базиса в новый. Матрица перехода из старого базиса в новый позволяет пересчитывать новые координаты в старые.

cos^A sin<p y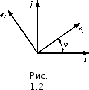

Пример 1.16. Рассмотрим в ортонормированный базис из векторов осей координат. Обозначим через новый базис, который получается поворотом старого базиса b на заданный угол . Исходя из заданного угла поворота, мы можем найти координаты векторов нового базиса относительно старого

Эти разложения позволяют составить матрицу перехода U из старого базиса b в новый e, а также обратную матрицу:

Найденные матрицы перехода U (из старого базиса в новый) и (из нового базиса в старый) позволяют записать соотношения между старыми и новыми , координатами произвольного вектора х из :

Например, вектор в старом базисе имеет координаты 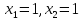, а в новом базисе - ,

Вопросы и задачи

1.1. Найдите координаты вектора х в базисе , если известны его координаты 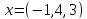в базисе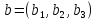, а базисы связаны соотношениями

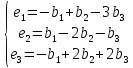
1.2. В линейном пространстве две системы векторов и заданы своими координатами в некотором базисе:

Докажите, что эти системы являются базисами. Найдите:

а) матрицу перехода от базиса b к базису е;

б) матрицу обратного перехода от базиса е к базису b;

в) координаты вектора в обоих базисах;

г) координаты вектора в базисе е.

1.3. Найдите размерность линейного пространства матриц типа с элементами из R.

1.4. Является ли матрица матрицей перехода от одного базиса трехмерного линейного пространства к его другому базису?

1.5. Какой вид имеет матрица перехода от старого базиса к новому, если матрица перехода от нового базиса к старому является:

а) треугольной; б) симметрической; в) кососимметрической?

1.5. Может ли в пространстве матрица перехода быть кососимметрической?

1.6. При каких условиях векторы в пространстве образуют базис?

1.7. Докажите, что в линейном пространстве многочлены

,

образуют базис. Найти координаты произвольно взятого многочлена в этом базисе.