
Программирование / си++ / ЛЕКЦИИ АСУ-03 за 1й курс / II cemecTP / Шпоры по матану / 56_60 / 56-60
.doc|
Функции f (х), имеющей все производные до (п + 1)-го порядка включительно, в окрестности точки х = а справедлива формула Тейлора:
Где Rn(x) остаточный член. Если функция f(х) имеет производные всех порядков в окрестности точки х = а, то в формуле Тейлора число п можно брать сколь угодно большим. Допустим, что в рассматриваемой окрестности остаточный член Rп→0 при n→∞:
Тогда, переходя в формуле (1) при n→∞, получим бесконечный ряд, который называется рядом Тейлора: (формула (1) без Rn(x).)(2) Если в ряде Тейлора а=0,то это ряд Маклорена: (формула (2) только a=0) Примеры разложения:
Биноминальный ряд:
Не берущиеся интегралы:
|
(57)Ортогональные системы функций, сходимость в среднем, понятие ряда Фурье. Опр.: Система функций φ1(х), φ2(х) … φn(х) (эти ф-ции определены и непрерывны на [a, b]) называется ортогональной в интервале [a, b], если интеграл от произведения любых двух различных функций системы =0: (1)
Ряд Фурье по ортог. сист. ф-ий: f(x)=∑(от n=0до ∞)cnφn(x).Ряд сходится в среднем если сред. квадратичное уклонение этой суммы→0: (2) Опр.: Ряд вида
где a0, an, bn, - заданные числа, называется тригонометрическим рядом, а заданные числа называются коэффициентами ряда. Опр.: Пусть f(x) – периодическая ф-ция с периодом 2π, интегрируемая на отрезке [-π,π], тогда числа
Называются коэффициентами Фурье(их вывод в билете 58) для ф-ции f(x), а тригонометрический ряд (1) с этими коэффициентами называется рядом Фурье ф-ции f(x). Опр.: Ф-ции f(x) называется кусочно монотонной на отрезке [a,b], если этот отрезок можно разбить на конечно число частей, внутри каждой из которых функция f(x) является монотонной. Эта ф-ция может иметь точки разрыва только 1-го рода. Если x=c точка разрыва то сущ. пределы:
Теор.(Теорема Дирихле) если f(x) периодом 2π -- кусочно монотонная и огран. на [-π,π] то ряд Фурье сходится во всех точках и S(x)=f(x), а если x – точка разрыва ф-ции f(x), S(x)=1/2(f(x-0)+f(x+0)), где S(x)-сумма ряда Фурье. (теор. дана без док-ва) Если f(x) четная то ряд состоит только из cos (bn=0), если f(x) нечетн.то ряд сост. из sin (a0=0 и an=0) |
(58) Тригонометрические ряды Фурье. Опр.: Ряд вида
где a0, an, bn, - заданные числа, называется тригонометрическим рядом, а заданные числа называются коэффициентами ряда. Пусть некотор. ф-ция f(x) с периодом 2π представляется тригоном. рядом: f(x)=(формула (1)) (2). Предположим, что интеграл от функции, стоящей в левой части эгого равенства, равняется сумме интегралов от членов ряда (2).Это выполняется если числовой ряд из коэфф. абсолютно сходится: |a0/2|+|a1|+|b1|+…+|an|+|bn|+…(3). Тогда ряд (1) мажорируем=>эго можно интегрировать от –π до π. Проинтегрируем равенство (2): ∫-ππf(x)dx = ∫-ππ(a0/2)dx+∑(n=0до∞)(∫-ππancos nx dx+∫-ππbnsin nx dx)(2`). Вычислим отдельно каждый интеграл: ∫-ππ(a0/2)dx=πa0, ∫-ππancos nx dx=an∫-ππcos nx dx= (ansin nx/n)| -ππ=0 ∫-ππbnsin nx dx=bn∫-ππsin nx dx= (ancos nx/n)| -ππ=0 следовательно ∫-ππf(x)dx=πa0, откуда a0=(1/π) ∫-ππf(x)dx(4). Далее потребуются след. интегралы: (n и k-целые числа). Если n≠k, то ∫-ππ cos nx cos kx dx=0; ∫-ππbnsin nx sin kx=0; ∫-ππ cos nx sin kx=0(I). Если n=k, то ∫-ππ cos2 kx=π; ∫-ππ sin2 kx=π; ∫-ππ cos kx sin kx=0 (II). Для разыскания ak умножим (2`) на cos kx: ∫-ππf(x) cos kx dx=(a0/2)∫-ππ cos kx dx+∑(n=0до∞)(∫-ππancosnx cos kx dx+∫-ππbnsin nx cos kx dx). Ввиду(I) и (II) все коэф в правой части=0 кроме интеграла с ak=>∫-ππf(x) cos kx dx= ak∫-ππ cos2 kx= akπ => ak= (1/π) ∫-ππf(x) cos kx dx(5) Для разыскания bk умножим (2`) на sin kx: bk= (1/π) ∫-ππf(x) sin kx dx(6). Тригонометрическим ряд с коэф (4)-(6)называется рядом Фурье ф-ции f(x).Теор. Дирихле в билете 57. Примеры:1) f(x)=x, -π<x≤π. Ряд: f(x)=2[sinx-sin2x/2+ sin3x/3-…+(-1)k+1(sin kx /k)+…] 2)f(x)=x при -π≤x≤0 и f(x)=-x при 0<x≤π. Ряд: f(x)=π/2- π/4[cosx+cos3x/32+cos5x/52+…+cos(2p+1)x/(2p+1)2+…] 3) f(x)=-1 при -π≤x≤0 и f(x)=1 при 0<x≤π. Ряд: f(x)= 4/π[sinx+sin3x/3+sin5x/5+…+ sin(2p+1)x/(2p+1)+…] 4) f(x)=x2, -π<x≤π. Ряд: f(x)=π2/3-4(cos x-cos2x/22+cos3x/32 -…), пологая что x=π: π2/6=∑(n=1до ∞)(1/n2) |
(59)Условие сходимости рядов Фурье. Докажем что если в окрестности x0 функция f(x) такова, что существуют конечные пределы: limα→-0(f(x0+α)-f(x0))/α=k1(1), limα→+0(f(x0+α)-f(x0))/α=k2(2). А в самой точке x0 функция непрерывна (рис. 388)(k1=tgφ1, k2= tgφ2),то в этой точке ряд Фурье сходится к соответ. значению ф-ии f(x). Доказательство. Рассмотрим ф-цию Ф(α): Ф(α)= [f(x0+α)- f(x0)](cosα/2/2sinα/2) так как функция f(х) кусочно непрерывна на отрезке [-π, π] и непрерывна в точке хо, то, следовательно, она непрерывна в некоторой окрестности [х0 -δ, х0+δ] точки х0. Поэтому функция Ф(α) непрерывна во всех точках, где α≠0 и |α| < δ. При α = 0 функция Ф (α) не определена. Найдем пределы limα→-0 Ф(α) и limα→+0 Ф(α) используя условия (1) и (2): limα→-0Ф(α)= limα→-0[f(x0+α)- f(x0)](cosα/2/2sinα/2)= limα→-0(f(x0+α)-f(x0))/α limα→-0α/2sinα/2 limα→-0cosα/2= k1*1*1= k1 Таким образом Ф(α) ограничена и непрерывна в про-межутке [-δ ,0] аналогично limα→-0 Ф(α)= k2 .Ф(α) огран. и непр в промежутке [0,δ]=> Ф(α) огран. и непр в[-δ,δ] Таким образом limn→∞[sn(x0)-f(x0)]=limn→∞(1/π)∫-δδФ(α) sin nα dα. Стоящий справа предел равен нулю, а поэтому limn→∞[sn(x0)-f(x0)]=0, или limn→∞sn(x0)= f(x0) Теорема доказана. |
(60) Понятие интеграла и преобразований Фурье. Пусть функция f (х) определена на бесконечном интервале (-∞, ∞) и абсолютно интегрируема на нем, т. е. существует интеграл: ∫-∞+∞|f(x)|dx=Q(1). Пусть f(x) разлагается на (-l,l) в ряд Фурье: f(x)=a0/2+ ∑(k=1 до ∞) (akcos(kπx/l)+ bksin(kπx/l))(2), где ak=(1/l)∫-llf(t)cos(kπt/l)dt, bk=(1/l)∫-llf(t)sin(kπt/l)dt(3). Подставляя в ряд (2) выражения коэффициентов ak и bk (3), можно написать: f(x)=(1/2l)∫-llf(t)dt+(1/l)∑(k=1 до ∞)(∫-llf(t)cos(kπt/l)dt) cos(kπx/l)+(1/l)∑(k=1 до ∞)(∫-llf(t)sin(kπt/l)dt)sin(kπx/l)= (1/2l)∫-llf(t)dt+(1/l)∑(k=1до∞)(∫-llf(t)[cos(kπt/l)dt)cos(kπx/l) +sin(kπt/l)dt)sin(kπx/l)]dt или f(x)=(1/2l)∫-llf(t)dt+ ∑(k=1до∞)(∫-llf(t)cos(kπ(t-x)/l)dt (4). Исследуем вопрос о том, какой вид примет разложение (4) при переходе к пределу при l →∞. Введем следующие обозначения: α1=π/l, α2=2π/l,…, αn=nπ/l и ∆αk=π/l.(5) Подставляя в (4), получаем: f(x)= (1/2l)∫-llf(t)dt+(1/l)∑(k=1до∞)(∫-llf(t)cosαk(t-x)dt)∆αk.(6) При l→∞ первый член в правой части стремится к нулю. При любом фиксированном l функция от ak (см. формулы (5)), принимающего значения от π/l до ∞. Без доказательства укажем, что если ф-ция f(х) кусочно монотонна на каждом конечном интервале, ограничена на бесконечном интервале и удовлетворяет условию (1), то при l→+∞ формула (6) примет вид: f(х)= (1/π)∫0+∞(∫-∞+∞f(t)cosαk(t-x)dt)dα(7). Это выражение называется интегралом Фурье для функции f(х). Равенство (7) имеет место для всех точек, где ф-ция непрерывна. В точках разрыва =(f(x+0)+f(x-0))/2. Пусть f(x) — четная функция. В этом случае f(t) cosαt — функция четная, f(t) sinαt — нечетная и мы получаем: f(x)=(2/π)∫0+∞(∫0+∞f(t)cos αt dt) cos αx dα.(8) Положим F(α)=√[2/π] ∫0+∞ f(t)cos αt dt.(9) тогда формула (8) примет вид f(x)= √[2/π] ∫0+∞F(α) cos αx dx(10) Функция F(α) называется косинус-преобразованием Фуръе для f(x). Аналогично Ф(α)= √[2/π] ∫0+∞ f(t)sin αt dt (11); f(x)= √[2/π] ∫0+∞Ф(α) sin αx dx синус-преобразованием Фуръе Пример: f(x)=e-βx (β>0, x≥0) F(α)= √[2/π] ∫0+∞e-βx cos αt dt=√[2/π] β(β2+α2) Ф(α)= √[2/π] ∫0+∞e-βx sin αt dt=√[2/π] α(β2+α2) |

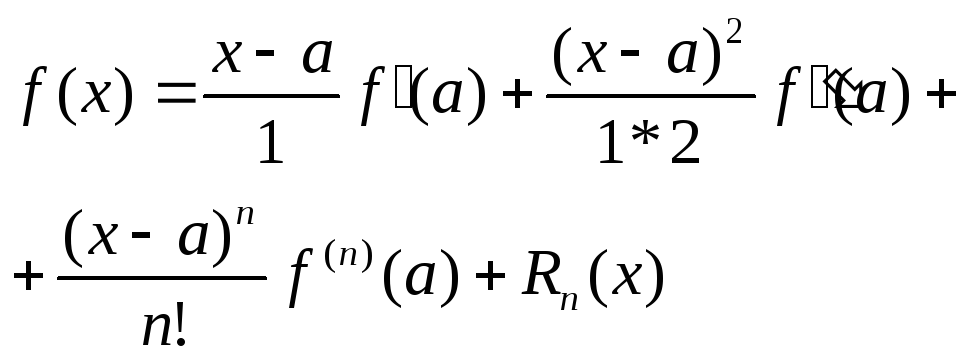 (1)
(1)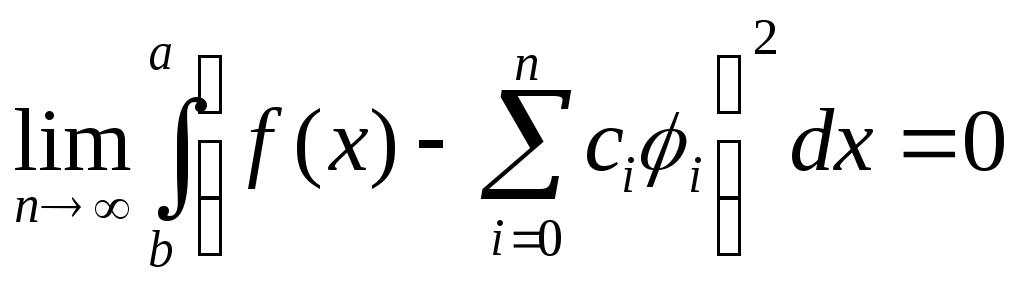 (2)
(2)