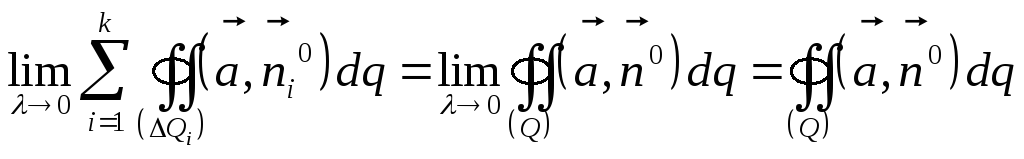|
(46)Поверхностный
интеграл 2-го порядка, свойства,
вычисление
Пусть
(Ф) - ориентированная ограниченная
гладкая поверхность (Q),
тогда

(
 дифференциал площади поверхности)
называется поверхностным
интегралом второго рода.
дифференциал площади поверхности)
называется поверхностным
интегралом второго рода.
В
случае замкнутости линии (L)
или поверхности (Q)
соответствующие интегралы по фигуре
обозначают
 и
и
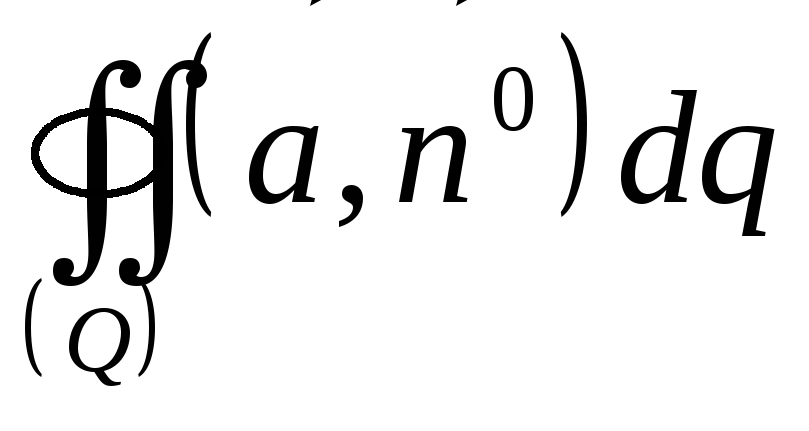
Свойства
интеграла по фигуре от векторной
функции.
Интеграл
по фигуре от алгебраической суммы
векторных функций равен алгебраической
сумме интегралов от слагаемых функций
по той же фигуре:
Постоянный
множитель можно выносить за знак
интеграла по фигуре
Если
фигура (Ф) представима в виде суммы
двух фигур
 и
и
 то интеграл по фигуре (Ф) равен сумме
интегралов по фигурам
то интеграл по фигуре (Ф) равен сумме
интегралов по фигурам
 и и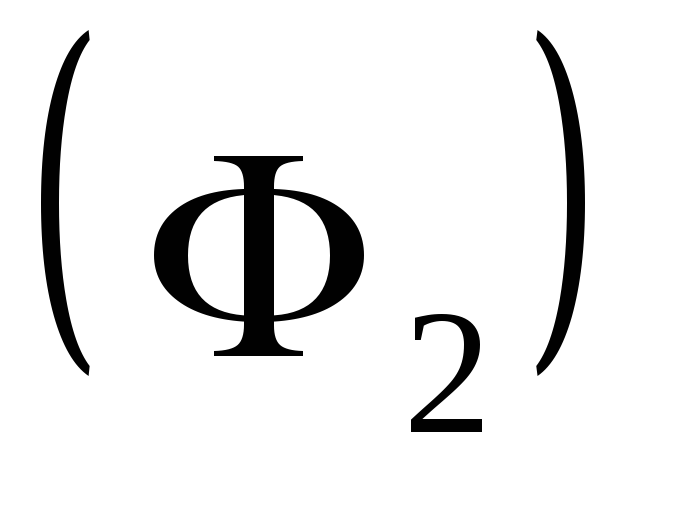 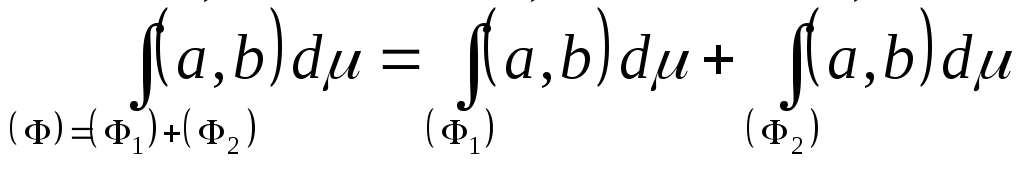 При
изменении направления ориентирующего
вектора При
изменении направления ориентирующего
вектора
 на противоположное (изменение ориентации
фигуры) интеграл по фигуре меняет
знак:
на противоположное (изменение ориентации
фигуры) интеграл по фигуре меняет
знак:
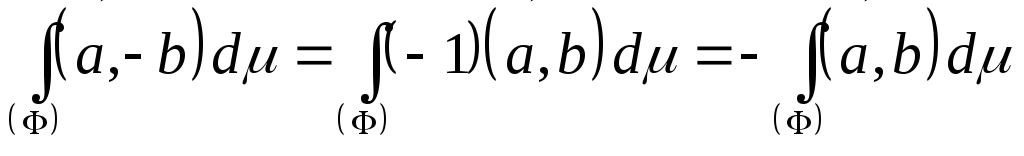
Скалярная
форма
поверхностного интеграла второго
рода.
Преобразуем
подынтегральное выражение в интеграле
 ,
учтем, что ,
учтем, что
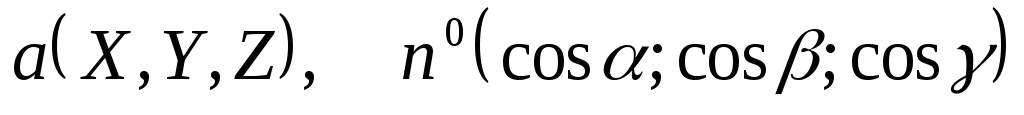 ,
где ,
где
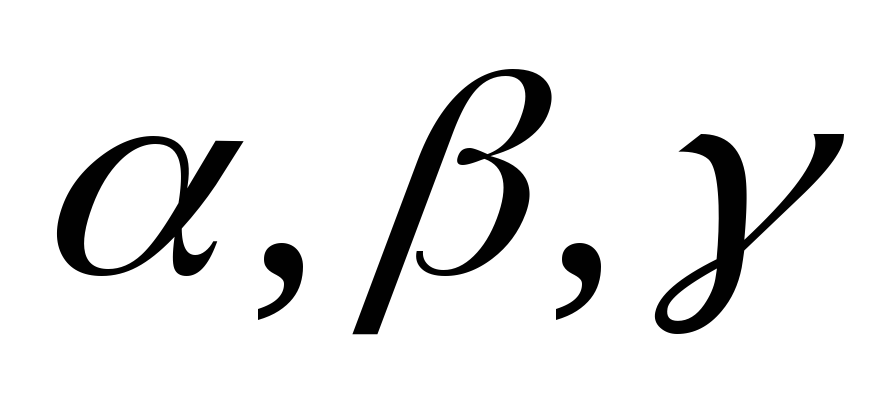 -углы
между вектором единичной нормали к
одной из выбранной сторон поверхности
и осями координат, -углы
между вектором единичной нормали к
одной из выбранной сторон поверхности
и осями координат,
 дифференциал поверхности.
дифференциал поверхности.
 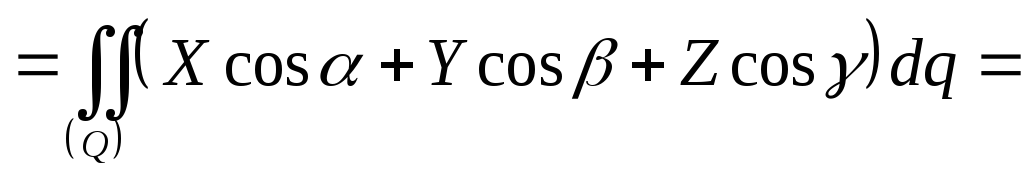 
Выражение
называют скалярной
формой поверхностного интеграла
второго рода.
Вычисление
поверхностного интеграла второго
рода.
Скалярная
форма может быть использована для
вычисления поверхностного интеграла
второго рода.
Отметим,
что произведение
 представляет собой взятую со знаком
"+" или "-" проекцию площади
представляет собой взятую со знаком
"+" или "-" проекцию площади
 поверхности (Q)
на плоскость Оху, т.е.
поверхности (Q)
на плоскость Оху, т.е.
 . .
Знак
"+" соответствует острому углу
между положительным направлением OZ
(нормалью к плоскости ОХУ) и вектором
 (нормалью к поверхности (Q)),
знак "-" соответствует тупому
углу. Аналогично
(нормалью к поверхности (Q)),
знак "-" соответствует тупому
углу. Аналогично
 , ,
 .
Приведенные результаты позволяют
свести вычисление интеграла (10) к
вычислению двойных интегралов по
плоским областям, являющимся проекцией
поверхности (Q)
на координатные плоскости .
Приведенные результаты позволяют
свести вычисление интеграла (10) к
вычислению двойных интегралов по
плоским областям, являющимся проекцией
поверхности (Q)
на координатные плоскости
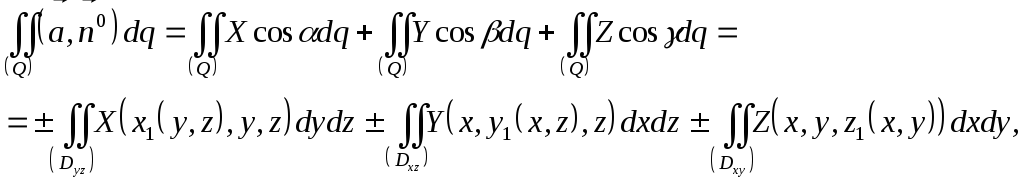 где где -
проекции поверхности (Q)
на плоскости Oxy,
Oxz,Oyz
соответственно. Функции -
проекции поверхности (Q)
на плоскости Oxy,
Oxz,Oyz
соответственно. Функции
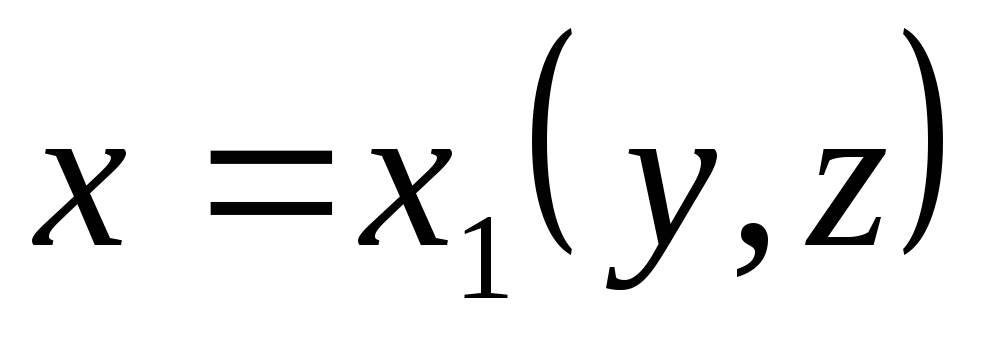 , ,
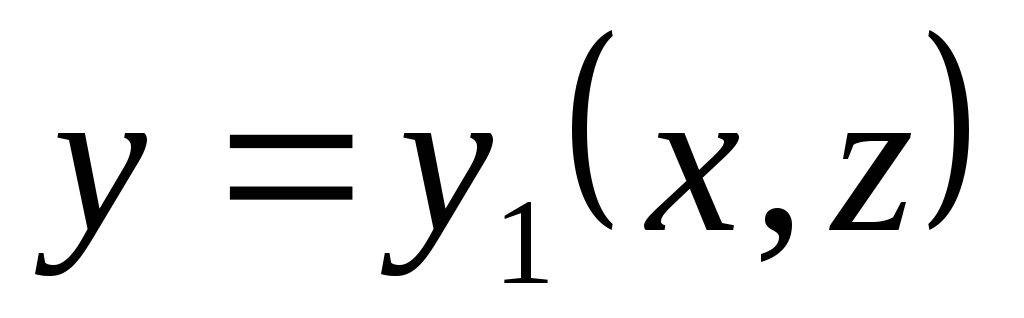 , ,
 получены из уравнения поверхности
(Q)
получены из уравнения поверхности
(Q)
 путем разрешения его относительно
переменных
путем разрешения его относительно
переменных
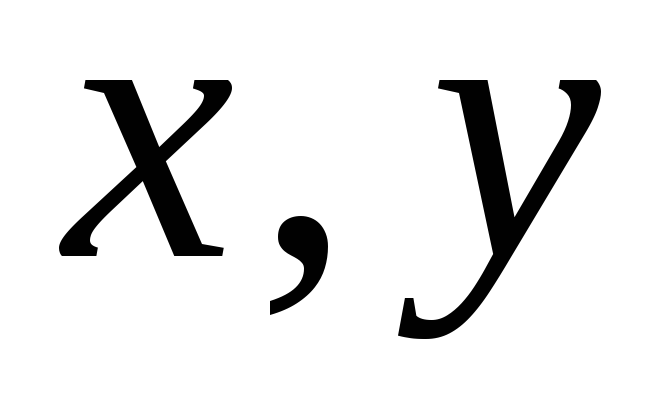 и
и
 . .
Замечание
Если
поверхность такова, что прямая,
параллельная какой либо из координатных
осей пересекает ее более чем одной
точке, то поверхность необходимо
разбить на сумму нескольких "правильных"
поверхностей.
|
(48)Формулы
Остроградского – Гаусса
Теорема
(Остроградского
- Гаусса) Если
векторная функция
 непрерывно дифференцируема в области
(V),
ограниченной замкнутой поверхностью
(Q),
то поток векторного поля
непрерывно дифференцируема в области
(V),
ограниченной замкнутой поверхностью
(Q),
то поток векторного поля
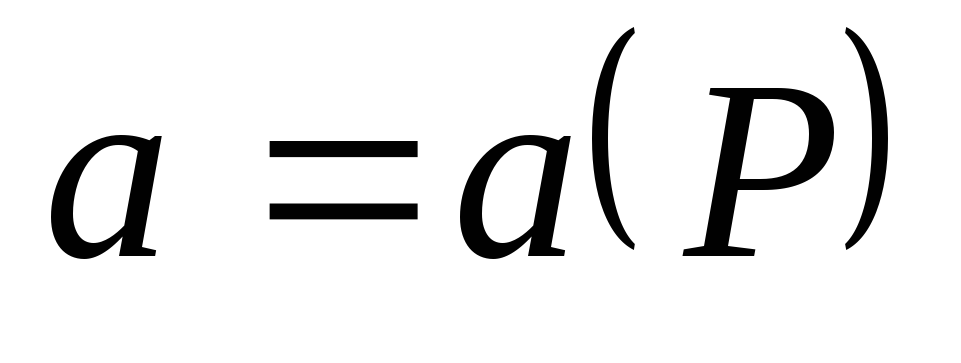 через поверхность (Q)
в направлении внешней нормали равен
тройному интегралу по области (V)
от дивергенции этого векторного поля,
т.е.
через поверхность (Q)
в направлении внешней нормали равен
тройному интегралу по области (V)
от дивергенции этого векторного поля,
т.е.

Доказательство
будем основывать на теореме о разностью
между функцией и ее конечным пределом.
Для этого разобьем область (V)
на k
элементарных областей
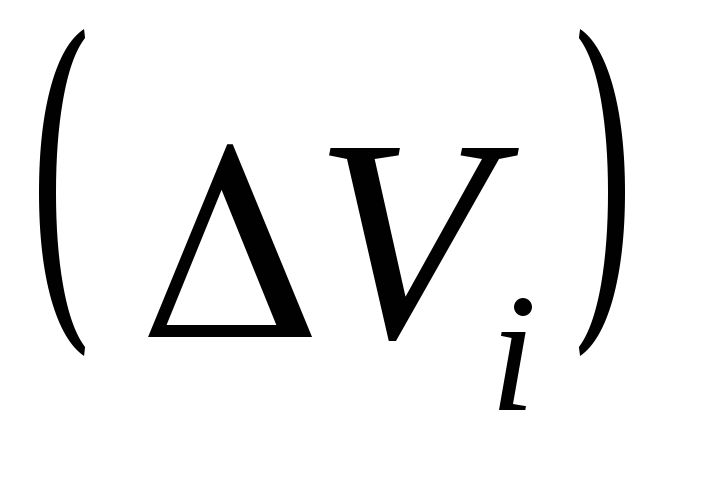 ,
границами которых являются поверхности ,
границами которых являются поверхности
 ,
а внешними единичными нормалями -
векторы ,
а внешними единичными нормалями -
векторы
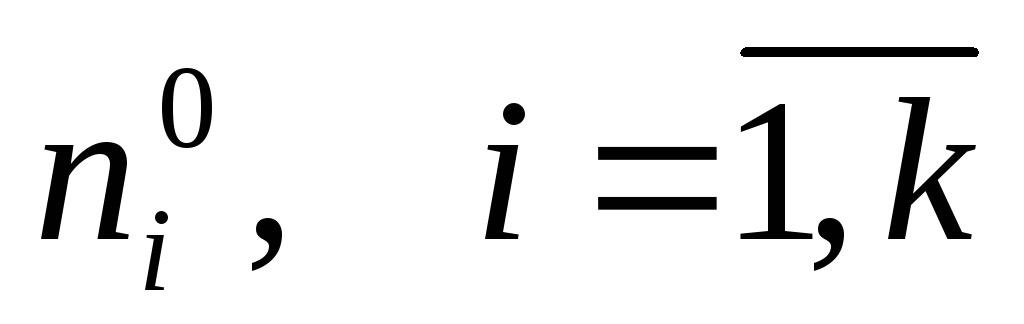 . .
Если
функция
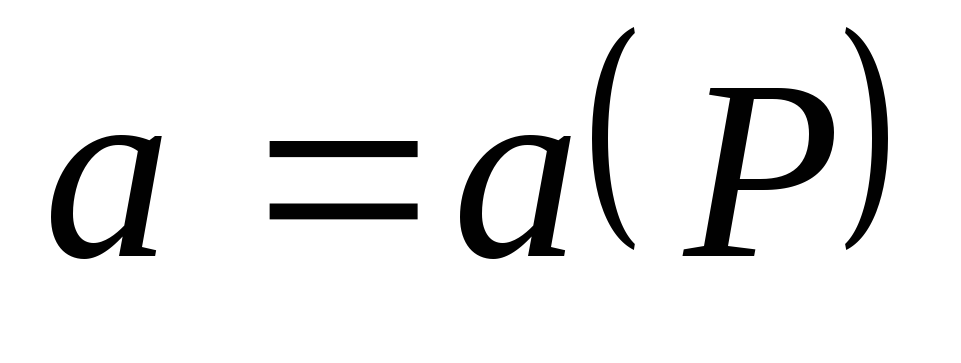 непрерывно
дифференцируема
в
области (V),
то в каждой точке этой области существует
непрерывно
дифференцируема
в
области (V),
то в каждой точке этой области существует
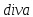 ,
являющаяся непрерывной функцией
координат точки Р. Тогда для элементарной
области ,
являющаяся непрерывной функцией
координат точки Р. Тогда для элементарной
области
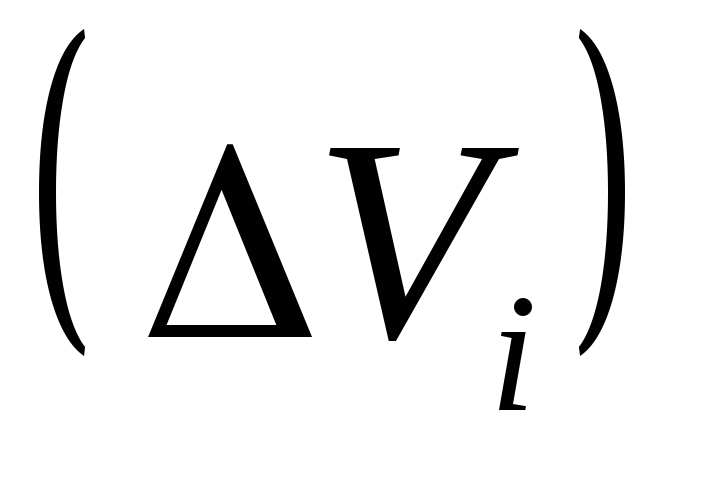 на основании формулы (17) имеем
на основании формулы (17) имеем
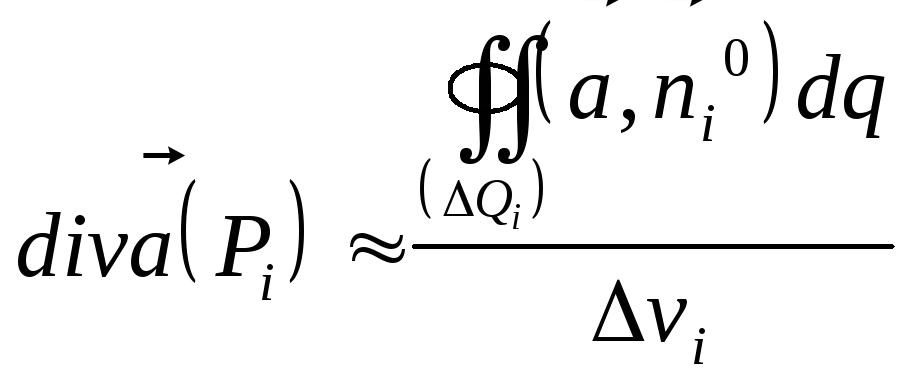 . .
Умножим
обе части на
 и воспользовавшись указанной выше
теоремой, получаем
и воспользовавшись указанной выше
теоремой, получаем
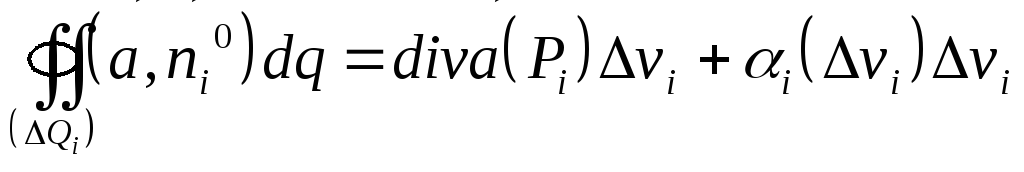 ,
(21) ,
(21)
где
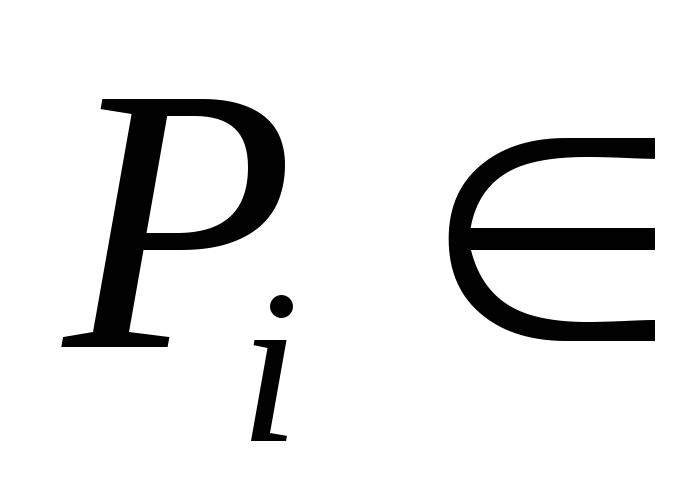  , ,
 -
бесконечно малая при -
бесконечно малая при
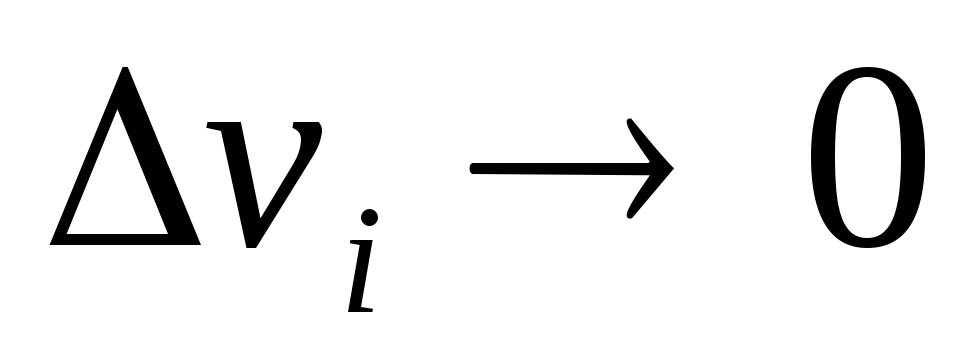 ; ;
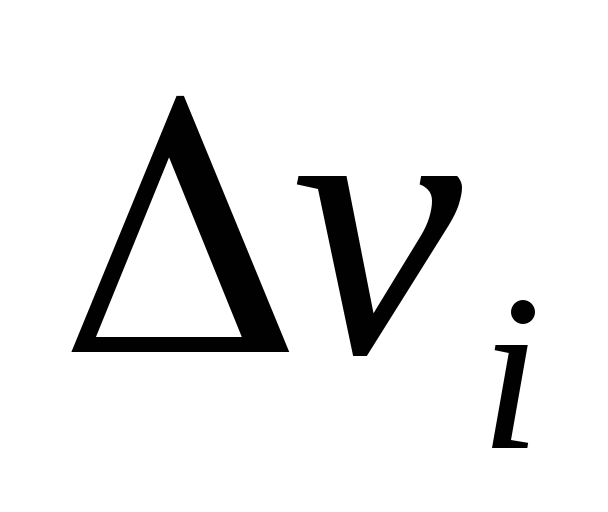 -
объем элементарной области -
объем элементарной области
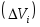 .
Просуммировав равенства (21), получаем .
Просуммировав равенства (21), получаем
 Отметим, что внешние нормали граней
Отметим, что внешние нормали граней
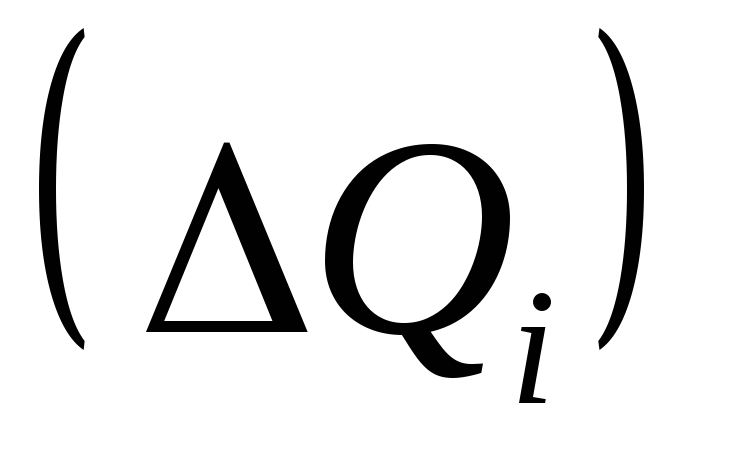 ,
соприкасающихся друг с другом,
противоположно направлены, и поэтому
потоки вектора ,
соприкасающихся друг с другом,
противоположно направлены, и поэтому
потоки вектора
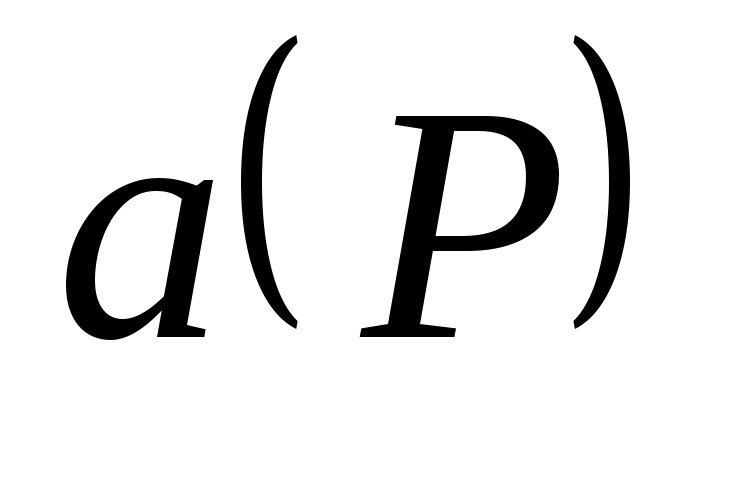 через "перегородки" в сумме равны
нулю. Следовательно в левой части
равенства (22) будет стоять величина
потока через поверхность (Q):
через "перегородки" в сумме равны
нулю. Следовательно в левой части
равенства (22) будет стоять величина
потока через поверхность (Q):

Перейдем
к пределу в равенстве (22) при условии
 или, что тоже самое
или, что тоже самое
 . .
 Рассмотрим
значения пределов Рассмотрим
значения пределов
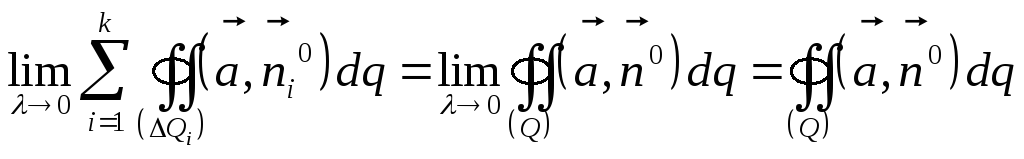 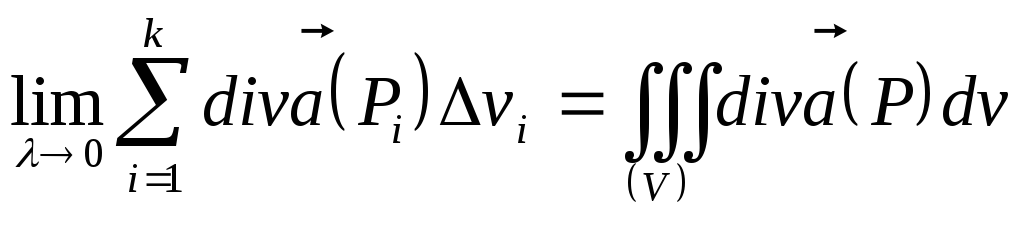 Обозначим Обозначим
 .
Тогда .
Тогда
 . .
Таким
образом предельное равенство приведено
к виду
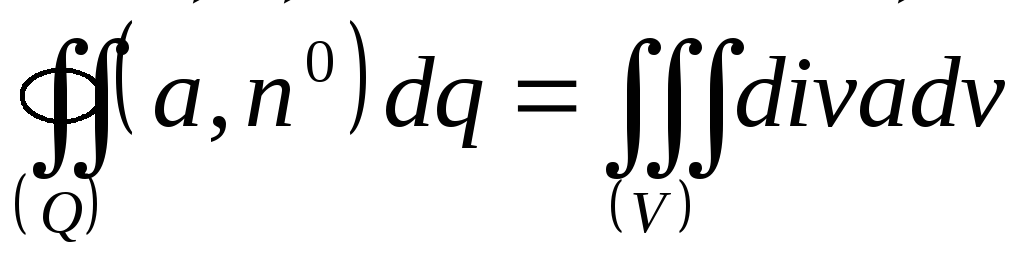 . .
Для
практики удобно скалярное представление
правой части
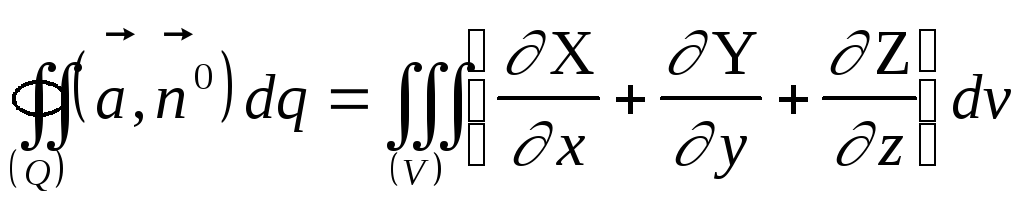
|
(47)Формула
Грина
Эта
формула обобщает формулу Ньютона-Лейбница.
Теорема
1. Пусть
G
- криволинейная трапеция:
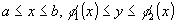 ,
где ,
где
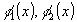 -
непрерывные на -
непрерывные на
 функции,
L
- граница области G
и направление обхода L
выбрано так, что область G
остается слева.
Пусть функции,
L
- граница области G
и направление обхода L
выбрано так, что область G
остается слева.
Пусть
 .
Тогда .
Тогда
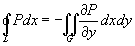 .
Знак .
Знак
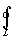 означает,
что контур интегрирования L
- замкнутый.
Доказательство.
Вычислим означает,
что контур интегрирования L
- замкнутый.
Доказательство.
Вычислим
 .
При каждом фиксированном .
При каждом фиксированном
 величина величина
 определяется,
как производная по y
функции от одной переменной y,
P(x,y).
Поэтому при каждом x
применима формула Ньютона-Лейбница,
согласно которой определяется,
как производная по y
функции от одной переменной y,
P(x,y).
Поэтому при каждом x
применима формула Ньютона-Лейбница,
согласно которой
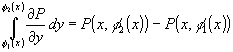 .
Поэтому .
Поэтому
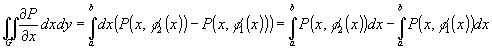 .
Разобъем кривую L
на 4 участка. .
Разобъем кривую L
на 4 участка.
 . .
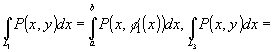 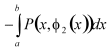 .
Поэтому .
Поэтому
  .
Теорема
2. Пусть
G
- криволинейная трапеция .
Теорема
2. Пусть
G
- криволинейная трапеция
 ,
где ,
где
 -
непрерывные на -
непрерывные на
 функции,
L
- граница G,
а направление обхода L
выбрано так, что G
остается слева.
Пусть функции,
L
- граница G,
а направление обхода L
выбрано так, что G
остается слева.
Пусть
 .
Тогда .
Тогда
 .
Доказательство. .
Доказательство.
  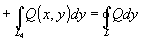 .
Теорема доказана. Следствие
1. Если
область G
можно представить как в виде трапеции .
Теорема доказана. Следствие
1. Если
область G
можно представить как в виде трапеции
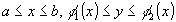 ,
где ,
где
 -
непрерывно дифференцируемые на -
непрерывно дифференцируемые на
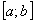 функции,
так и в виде функции,
так и в виде
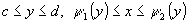 ,
где ,
где
 -
непрерывно дифференцируемые на -
непрерывно дифференцируемые на
 функции,
L
- граница G,
причем при ее обходе область G
остается слева, то функции,
L
- граница G,
причем при ее обходе область G
остается слева, то
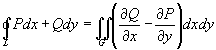 .
Примечание.
Области, удовлетворяющие условиям
следствия 1 - явление обычное. Например,
круг .
Примечание.
Области, удовлетворяющие условиям
следствия 1 - явление обычное. Например,
круг
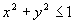 ,
ограниченный окружностью ,
ограниченный окружностью
 ,
можно задать так: ,
можно задать так:
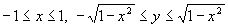 ,
а можно и так: ,
а можно и так:
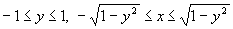 .
Следствие
2. Если
область G
можно разбить кривыми на конечное
число областей, удовлетворяющих
условиям следствия 1 и L
- граница G,
причем направление обхода выбрано
так, что область G
остается слева, и P
и Q
удовлетворяют перечисленным выше
условиям, то .
Следствие
2. Если
область G
можно разбить кривыми на конечное
число областей, удовлетворяющих
условиям следствия 1 и L
- граница G,
причем направление обхода выбрано
так, что область G
остается слева, и P
и Q
удовлетворяют перечисленным выше
условиям, то
 .
Доказательство.
Ограничимся
случаем, когда область G
разбивается на 2 части .
Доказательство.
Ограничимся
случаем, когда область G
разбивается на 2 части
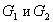 ,
удовлетворяющие условиям следствия
1, кривой ,
удовлетворяющие условиям следствия
1, кривой
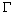 .
Пусть .
Пусть
 ограничивает ограничивает
 ,
а ,
а
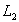 ограничивает ограничивает
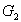 .
Тогда .
Тогда
 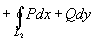 ,
поскольку ,
поскольку
 -
это часть L
и кривая -
это часть L
и кривая
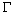 ,
а ,
а
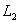 -
остаток L
и кривая -
остаток L
и кривая
 ,
но проходимая в противоположном
направлении (поэтому интегралы по
этим добавленным участкам сократятся).
Замечание.
Можно доказать формулу Грина для
областей, ограниченных замкнутыми
кусочно-гладкими кривыми. ,
но проходимая в противоположном
направлении (поэтому интегралы по
этим добавленным участкам сократятся).
Замечание.
Можно доказать формулу Грина для
областей, ограниченных замкнутыми
кусочно-гладкими кривыми.
|
(49)Понятие и
необходимый признак сходимости
числового ряда
Определение
числового ряда.
Сходимость ряда.
Бесконечным
числовым рядом
называется выражение
u1+u2+...+un+...
содержащее
неограниченное число членов, где
u1
, u2
, u3
, ... , un
, ...
-
бесконечная числовая последовательность;
un
называется общим
членом ряда.
Для
составления ряда нужно знать закон
образования общего члена.
Например,
если un
= 2*n+1,
то ряд имеет вид:
3, 5, 7, 9, ..., 501,
503, ..., n*2+1
Если
un
= (-1)n,
то ряд имеет вид:
-1,
+1, -1, +1, ..., -1, +1, ..., (-1)n
Сумма
первых n
членов ряда обозначается символом Sn
и называется частичной
суммой
этого ряда. Таким образом,
Sn
= u1
+ u2
+ ... + u n
или, короче,
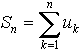
Определение:
Ряд называется сходящимся,
если сумма первых его n
членов при n
стремится к конечному пределу S,
называемому суммой
ряда.
Если ряд (1)
сходится, т.е. имеет сумму S,
то пишут
S =
u1
+ u2
+ ... + u n
+ ...
Если
же при n
сумма Sn
не имеет предела или
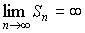
то
ряд (1)
называется расходящимся
и не имеет суммы.
Типичным
примером сходящегося ряда может
служить ряд, полученный из бесконечно
убывающей геометрической прогрессии
a + aq
+ aq
2
+ aq
3
+ ... + aq
n-1
+ ...,
где
-1 <
q
< 1
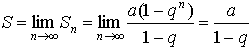
и ряд
(2)
будет сходящимся. Таким образом можно
написать
Если
q
= 1,
то ряд (2)
имеет вид
a
+ a + a + a + ... + a + ... .
Сумма
Sn
первых его n
членов, равная na,
по абсолютной величине неограниченно
возрастает при неограниченном
возрастании числа n.
Таким образом, ряд (3)
- расходящийся.
Если
q
= -1,
то
ряд
(2)
примет
вид
a
- a + a - a + a - a +... +(-1)n-1
a + ... .
Ясно, что для
этого ряда
S2n=0 , S2n-1=a.
т.е.сумма
четного числа первых 2n
членов ряда (4) стремится к нулю, а сумма
нечетного числа первых 2n-1
его членов стремится к a.
Отсюда
следует, что ряд (4) расходится, так как
в сходящемся ряде как S2n
так и S2n-1
стремятся к одному и тому же пределу
S.
Ясно,
что если | q
|>1, то ряд (2)
является также расходящимся.
Необходимый
признак сходимости числового ряда.
Теорема:
Пусть
числовой ряд
u1+u2+...+un+...
,
сходится,
а S - его сумма. Тогда при неограниченном
возрастании числа n членов ряда его
общий член un
стремится к нулю
Доказательство.
Из условия теоремы имеем
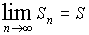 
Так как
Sn
- Sn-1
= un
то

Следует
отметить, что этот признак является
лишь необходимым, но не достаточным
признаком сходимости ряда, так как
можно указать ряд, для которого
выполняется равенство
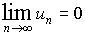 ,а
он, однако не является сходящимся.
Так
гармонический ряд ,а
он, однако не является сходящимся.
Так
гармонический ряд
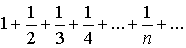 , ,
для которого
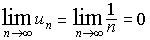 , ,
расходится.
Но
согласно доказанному необходимому
признаку сходимости ряда, если
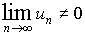 ,то
ряд (1)
расходится.
В самом деле, если
бы он сходился, то ,то
ряд (1)
расходится.
В самом деле, если
бы он сходился, то
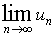 равнялся
бы нулю.
Таким образом,
доказанная нами теорема иногда
позволяет, не вычисляя суммы Sn,
сделать заключение о расходимости
того или иного ряда. Например, ряд равнялся
бы нулю.
Таким образом,
доказанная нами теорема иногда
позволяет, не вычисляя суммы Sn,
сделать заключение о расходимости
того или иного ряда. Например, ряд
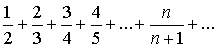 , ,
расходится, так
как
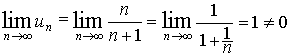
|
(50)Достаточные
признаки сравнения и сходимости
знакоположительных рядов
Если
известно, что все члены ряда
 имеют,
начиная с некоторого номера, постоянный
знак, то исследовать его сходимость
проще, чем в общем случае. Это связано
с простым критерием сходимости для
таких рядов. Для простоты предположим,
что все имеют,
начиная с некоторого номера, постоянный
знак, то исследовать его сходимость
проще, чем в общем случае. Это связано
с простым критерием сходимости для
таких рядов. Для простоты предположим,
что все
 .
Теорема.
(Критерий сходимости рядов с
неотрицательными членами). Ряд .
Теорема.
(Критерий сходимости рядов с
неотрицательными членами). Ряд
 сходится сходится
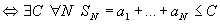 .
Доказательство. .
Доказательство.
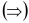 .
Пусть .
Пусть
 .
Тогда .
Тогда
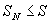 при
всех при
всех
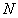 . .
 .
Пусть .
Пусть
 .
Поскольку .
Поскольку
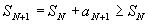 ,
последовательность ,
последовательность
 возрастает
и, по условию, ограничена. Следовательно,
по теореме Вейерштрасса (см. 1-ый
семестр), она имеет предел, то есть ряд
сходится. возрастает
и, по условию, ограничена. Следовательно,
по теореме Вейерштрасса (см. 1-ый
семестр), она имеет предел, то есть ряд
сходится.
Простые
следствия из этого критерия – очень
полезные теоремы сравнения. Теорема
1. Пусть
для всех
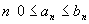 и
пусть ряд и
пусть ряд
 -
сходится. Тогда сходится ряд -
сходится. Тогда сходится ряд
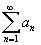 .
Доказательство.
Очевидны неравенства .
Доказательство.
Очевидны неравенства
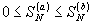 .
По условию .
По условию
 -
сходится. Значит, по приведенному выше
критерию, -
сходится. Значит, по приведенному выше
критерию,
 .
Но тогда и .
Но тогда и
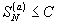 и,
значит, ряд и,
значит, ряд
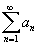 -
сходится.
Примечание
1. Эта
теорема может быть сформулирована и
так: Пусть для всех -
сходится.
Примечание
1. Эта
теорема может быть сформулирована и
так: Пусть для всех
 и
ряд и
ряд
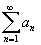 -
расходится, тогда расходится и ряд -
расходится, тогда расходится и ряд
 .
Действительно, если бы этот ряд
сходился, то первой теореме должен
был бы сходиться и ряд .
Действительно, если бы этот ряд
сходился, то первой теореме должен
был бы сходиться и ряд
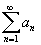 .
Примечание
2. Теорема
1 справедлива и в случае, когда
неравенство .
Примечание
2. Теорема
1 справедлива и в случае, когда
неравенство
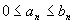 выполняется
начиная с некоторого номера выполняется
начиная с некоторого номера
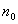 .
Теорема
2. Пусть .
Теорема
2. Пусть
 для
всех для
всех
 и и
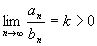 .
Тогда либо оба ряда .
Тогда либо оба ряда
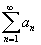 и и
 сходятся,
либо они оба расходятся. (Т.е. не может
быть так, что один из них сходится, а
другой расходится).
Доказательство. сходятся,
либо они оба расходятся. (Т.е. не может
быть так, что один из них сходится, а
другой расходится).
Доказательство.
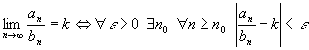 .
Выберем .
Выберем
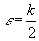 .
Тогда .
Тогда
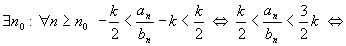 (т.к. (т.к.
 ) )
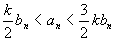 при при
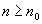 .
Если ряд .
Если ряд
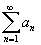 –
сходится, то сходится и ряд –
сходится, то сходится и ряд
 (по
примечанию 2 к теореме 1). Тогда, взяв (по
примечанию 2 к теореме 1). Тогда, взяв
 ,
получим, что и ряд ,
получим, что и ряд
 ,
т.е. ряд ,
т.е. ряд
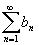 –
сходится. Если
ряд –
сходится. Если
ряд
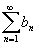 –
сходится, то сходится и ряд –
сходится, то сходится и ряд
 и,
следовательно, сходится ряд и,
следовательно, сходится ряд
 .
Теорема доказана.
Пример
применения теоремы 2. Ряд .
Теорема доказана.
Пример
применения теоремы 2. Ряд
 сходится,
т.к. сходится,
т.к.
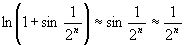 при при
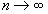 и
ряд и
ряд
 –
сходится.
Теорема.
(Признак сходимости Коши). Пусть –
сходится.
Теорема.
(Признак сходимости Коши). Пусть
 и
при достаточно больших и
при достаточно больших
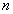  .
Тогда ряд .
Тогда ряд
 сходится.
Если же при сходится.
Если же при
  ,
то он расходится. Доказательство.
Неравенство ,
то он расходится. Доказательство.
Неравенство
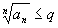 при при
 равносильно
неравенству равносильно
неравенству
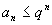 .
Так как .
Так как
 ,
ряд ,
ряд
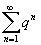 –
сходится. По теореме 1 из предыдущего
параграфа ряд –
сходится. По теореме 1 из предыдущего
параграфа ряд
 также
сходится.
Если же также
сходится.
Если же
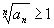 ,
то и ,
то и
 и
равенство и
равенство
 невозможно.
Т.о. необходимый признак сходимости
не выполняется и ряд расходится.
В предельной форме эта теорема
выглядит так:
Теорема.
Пусть существует невозможно.
Т.о. необходимый признак сходимости
не выполняется и ряд расходится.
В предельной форме эта теорема
выглядит так:
Теорема.
Пусть существует
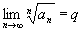 .
Тогда если .
Тогда если
 –
ряд сходится, –
ряд сходится,
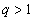 –
ряд расходится, –
ряд расходится,
 –
признак неприменим.
Доказательство.
Пусть –
признак неприменим.
Доказательство.
Пусть
 .
Выберем .
Выберем
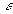 так,
чтобы так,
чтобы
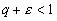 (т.е. (т.е.
 ).
Тогда при ).
Тогда при
  ,
т.е. ,
т.е.
 .
Применяя предыдущую теорему получаем,
что ряд сходится.
Если же .
Применяя предыдущую теорему получаем,
что ряд сходится.
Если же
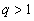 ,
то выберем ,
то выберем
 так,
что так,
что
 (т.е. (т.е.
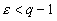 ).
Тогда ).
Тогда
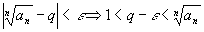 .
Вновь по предыдущей теореме ряд
расходится.
Теорема.
(Признак сходимости Даламбера). Пусть
при всех .
Вновь по предыдущей теореме ряд
расходится.
Теорема.
(Признак сходимости Даламбера). Пусть
при всех
 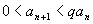 ,
где ,
где
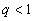 .
Тогда ряд сходится. Если же при .
Тогда ряд сходится. Если же при
  ,
то ряд расходится.
Доказательство.
Из условий теоремы следует ,
то ряд расходится.
Доказательство.
Из условий теоремы следует
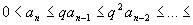  .
Иными словами, .
Иными словами,
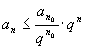 и
по первой теореме сравнения ряд
сходится. Если и
по первой теореме сравнения ряд
сходится. Если
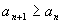 ,
то ,
то
 при при
 и
ряд расходится.
В предельной
форме этот признак выглядит так:
Теорема.
Если существует и
ряд расходится.
В предельной
форме этот признак выглядит так:
Теорема.
Если существует
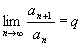 ,
то при ,
то при
 ряд
сходится, при ряд
сходится, при
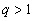 -
расходится, а при -
расходится, а при
 признак
неприменим.
Доказательство.
При признак
неприменим.
Доказательство.
При
 выбираем выбираем
 так,
чтобы так,
чтобы
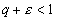 .
Пусть .
Пусть
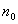 выбрано
так, чтобы при выбрано
так, чтобы при
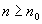  ,
т.е. ,
т.е.
 и и
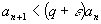 , ,
 .
По предыдущей теореме ряд сходится.
Если же .
По предыдущей теореме ряд сходится.
Если же
 ,
то выберем ,
то выберем
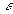 так,
что так,
что
 .
Тогда при .
Тогда при
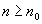 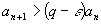 и
ряд расходится.
Признаки Коши и
Даламбера удобны, но слабоваты.
Например, для рядо и
ряд расходится.
Признаки Коши и
Даламбера удобны, но слабоваты.
Например, для рядо
 и и
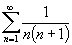 : :
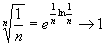 при при
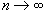 , ,
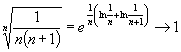 при при
 ,
т.е. признак Коши не применим. Признак
Даламбера тем более неприменим, т.к. ,
т.е. признак Коши не применим. Признак
Даламбера тем более неприменим, т.к.
 , ,
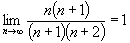 .
Однако
мы знаем, что гармонический ряд
расходится, а для второго ряда легко
подсчитать частичную сумму: .
Однако
мы знаем, что гармонический ряд
расходится, а для второго ряда легко
подсчитать частичную сумму:
 и и
 при при
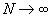 .
(Здесь использовано тождество .
(Здесь использовано тождество
 ),
т.е. ряд сходится. Теорема.
(признак Гаусса). Пусть ),
т.е. ряд сходится. Теорема.
(признак Гаусса). Пусть
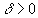 и и
 , ,
 .
В применении
к ряду .
В применении
к ряду
 она
дает: она
дает:
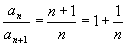 , ,
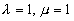 -
ряд расходится. Для ряда -
ряд расходится. Для ряда
 имеем: имеем:
 , ,
 -
ряд сходится. -
ряд сходится.
|



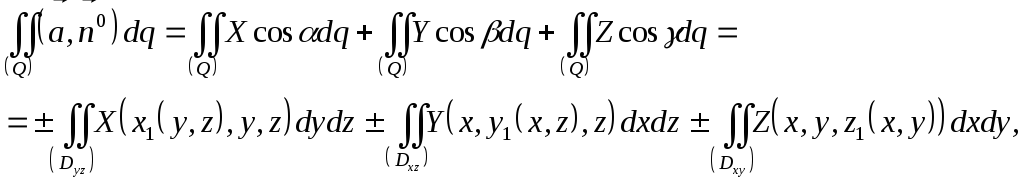 где
где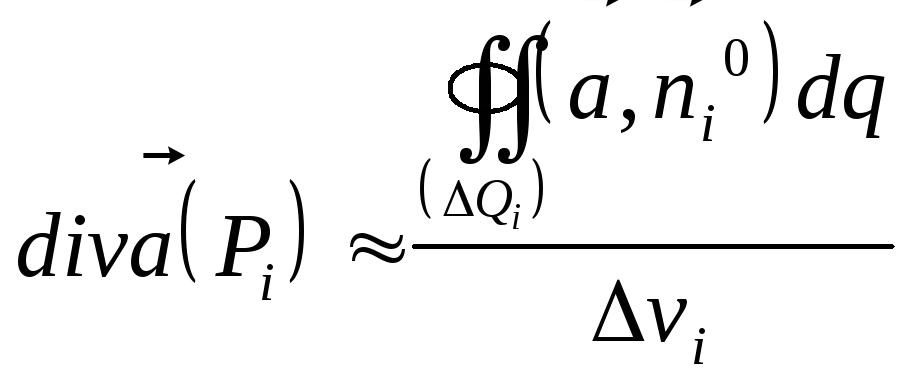 .
.
 Отметим, что внешние нормали граней
Отметим, что внешние нормали граней

 Рассмотрим
значения пределов
Рассмотрим
значения пределов