|
(47)
Формула Грина Эта
формула обобщает формулу Ньютона-Лейбница.
Теорема
1. Пусть
G
- криволинейная трапеция:
 ,
где ,
где
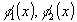 -
непрерывные на [a,b]
функции, L
- граница области G
и направление обхода L
выбрано так, что область G
остается слева Пусть -
непрерывные на [a,b]
функции, L
- граница области G
и направление обхода L
выбрано так, что область G
остается слева Пусть
 .
Тогда .
Тогда
 .
Знак .
Знак
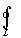 означает,
что контур интегрирования L
- замкнутый. означает,
что контур интегрирования L
- замкнутый.
Доказательство.
Вычислим
 .
При каждом фиксированном .
При каждом фиксированном
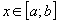 величина величина
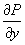 определяется,
как производная по y
функции от одной переменной y,
P(x,y).
Поэтому при каждом x
применима формула Ньютона-Лейбница,
согласно которой определяется,
как производная по y
функции от одной переменной y,
P(x,y).
Поэтому при каждом x
применима формула Ньютона-Лейбница,
согласно которой
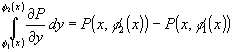 .
Поэтому .
Поэтому
 .Разобъем
кривую L
на 4 участка. .Разобъем
кривую L
на 4 участка.
 . .
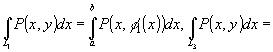 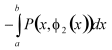 .
Поэтому .
Поэтому
  . .
Теорема 2.
Пусть G
- криволинейная трапеция
 ,
где ,
где
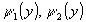 -
непрерывные на [c,d]
функции, L
- граница G,
а направление обхода L
выбрано так, что G
остается слева. Пусть -
непрерывные на [c,d]
функции, L
- граница G,
а направление обхода L
выбрано так, что G
остается слева. Пусть
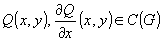 .
Тогда .
Тогда
 .
Доказательство. .
Доказательство.
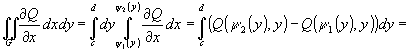   .
Теорема доказана. .
Теорема доказана.
Следствие 1.
Если область G
можно представить как в виде трапеции
 ,
где ,
где
 -
непрерывно дифференцируемые на [a,b]
функции, так и в виде -
непрерывно дифференцируемые на [a,b]
функции, так и в виде
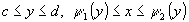 ,
где ,
где
 -
непрерывно дифференцируемые на
[c,d]функции,
L
- граница G,
причем при ее обходе область G
остается слева, то -
непрерывно дифференцируемые на
[c,d]функции,
L
- граница G,
причем при ее обходе область G
остается слева, то
 .
Примечание.
Области, удовлетворяющие условиям
следствия 1 - явление обычное. Например,
круг .
Примечание.
Области, удовлетворяющие условиям
следствия 1 - явление обычное. Например,
круг
 ,
ограниченный окружностью ,
ограниченный окружностью
 ,
можно задать так: ,
можно задать так:
 ,
а можно и так: ,
а можно и так:
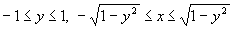 . .
Следствие 2.
Если область G
можно разбить кривыми на конечное
число областей, удовлетворяющих
условиям следствия 1 и L
- граница G,
причем направление обхода выбрано
так, что область G
остается слева, и P
и Q
удовлетворяют перечисленным выше
условиям, то
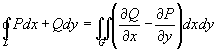 .
Доказательство.
Ограничимся
случаем, когда область G
разбивается на 2 части, G1
и G2
удовлетворяющие
условиям следствия 1, кривой Г. Пусть
L1
ограничивает G1,
а L2ограничивает
G2.
Тогда .
Доказательство.
Ограничимся
случаем, когда область G
разбивается на 2 части, G1
и G2
удовлетворяющие
условиям следствия 1, кривой Г. Пусть
L1
ограничивает G1,
а L2ограничивает
G2.
Тогда
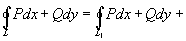  ,
поскольку L1-
это часть L
и кривая Г, а L2-
остаток L
и кривая Г, но проходимая в противоположном
направлении (поэтому интегралы по
этим добавленным участкам сократятся). ,
поскольку L1-
это часть L
и кривая Г, а L2-
остаток L
и кривая Г, но проходимая в противоположном
направлении (поэтому интегралы по
этим добавленным участкам сократятся).
Замечание.
Можно доказать формулу Грина для
областей, ограниченных замкнутыми
кусочно-гладкими
кривыми.
|
(50) Достаточные
признаки сравнения и сходимости
знакоположительных рядов
Если
известно, что все члены ряда
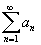 имеют,
начиная с некоторого номера, постоянный
знак, то исследовать его сходимость
проще, чем в общем случае. Это связано
с простым критерием сходимости для
таких рядов. Для простоты предположим,
что все an
>=0
Теорема.
(Критерий сходимости рядов с
неотрицательными членами). Ряд имеют,
начиная с некоторого номера, постоянный
знак, то исследовать его сходимость
проще, чем в общем случае. Это связано
с простым критерием сходимости для
таких рядов. Для простоты предположим,
что все an
>=0
Теорема.
(Критерий сходимости рядов с
неотрицательными членами). Ряд
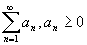 сходится сходится
 .
Доказательство.
(=>). Пусть .
Доказательство.
(=>). Пусть
 .
Тогда .
Тогда
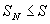 при
всех N.
(<=)
. Пусть при
всех N.
(<=)
. Пусть
 .
Поскольку .
Поскольку
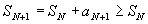 ,
последовательность Sn
возрастает и, по условию, ограничена.
Следовательно, по теореме Вейерштрасса
(см. 1-ый семестр), она имеет предел, то
есть ряд сходится. ,
последовательность Sn
возрастает и, по условию, ограничена.
Следовательно, по теореме Вейерштрасса
(см. 1-ый семестр), она имеет предел, то
есть ряд сходится.
Простые
следствия из этого критерия – очень
полезные теоремы сравнения. Теорема
1. Пусть
для всех
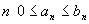 и
пусть ряд и
пусть ряд
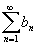 -
сходится. Тогда сходится ряд -
сходится. Тогда сходится ряд
 . .
Доказательство.
Очевидны неравенства
 .
По условию .
По условию
 -
сходится. Значит, по приведенному выше
критерию, -
сходится. Значит, по приведенному выше
критерию,
 .
Но тогда и .
Но тогда и
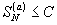 и,
значит, ряд и,
значит, ряд
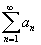 -
сходится. Примечание
1. Эта
теорема может быть сформулирована и
так: Пусть для всех -
сходится. Примечание
1. Эта
теорема может быть сформулирована и
так: Пусть для всех
 и
ряд и
ряд
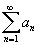 -
расходится, тогда расходится и ряд -
расходится, тогда расходится и ряд
 .
Действительно, если бы этот ряд
сходился, то первой теореме должен
был бы сходиться и ряд .
Действительно, если бы этот ряд
сходился, то первой теореме должен
был бы сходиться и ряд
 .
Примечание
2. Теорема
1 справедлива и в случае, когда
неравенство .
Примечание
2. Теорема
1 справедлива и в случае, когда
неравенство
 выполняется
начиная с некоторого номера выполняется
начиная с некоторого номера
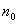 .
Теорема
2. Пусть .
Теорема
2. Пусть
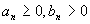 для
всех для
всех
 и и
 .
Тогда либо оба ряда .
Тогда либо оба ряда
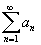 и и
 сходятся,
либо они оба расходятся. (Т.е. не может
быть так, что один из них сходится, а
другой расходится).
Доказательство. сходятся,
либо они оба расходятся. (Т.е. не может
быть так, что один из них сходится, а
другой расходится).
Доказательство.
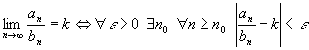 .
Выберем .
Выберем
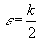 .
Тогда .
Тогда
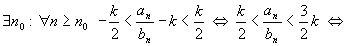 (т.к.bn>0) (т.к.bn>0)
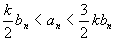 при
n>=n0.
Если ряд при
n>=n0.
Если ряд
 –
сходится, то сходится и ряд –
сходится, то сходится и ряд
 (по
примечанию 2 к теореме 1). Тогда, взяв (по
примечанию 2 к теореме 1). Тогда, взяв
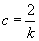 ,
получим, что и ряд ,
получим, что и ряд
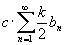 ,
т.е. ряд ,
т.е. ряд
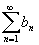 –
сходится. Если ряд –
сходится. Если ряд
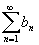 –
сходится, то сходится и ряд –
сходится, то сходится и ряд
 и,
следовательно, сходится ряд и,
следовательно, сходится ряд
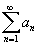 .
Теорема доказана.
Пример
применения теоремы 2. Ряд .
Теорема доказана.
Пример
применения теоремы 2. Ряд
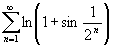 сходится,
т.к. сходится,
т.к.
 при при
 и
ряд и
ряд
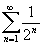 –
сходится. Теорема.
(Признак сходимости Коши). Пусть an
>=0
и при
достаточно больших –
сходится. Теорема.
(Признак сходимости Коши). Пусть an
>=0
и при
достаточно больших
  .
Тогда ряд .
Тогда ряд
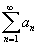 сходится.
Если же при сходится.
Если же при
 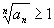 ,
то он расходится. Доказательство.
Неравенство ,
то он расходится. Доказательство.
Неравенство
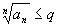 при
n>=n0
равносильно
неравенству при
n>=n0
равносильно
неравенству
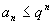 .
Так как .
Так как
 ,
ряд ,
ряд
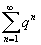 –
сходится. По теореме 1 из предыдущего
параграфа ряд –
сходится. По теореме 1 из предыдущего
параграфа ряд
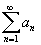 также
сходится.
Если же также
сходится.
Если же
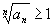 ,
то и an
>=1 и
равенство ,
то и an
>=1 и
равенство
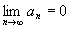 невозможно.
Т.о. необходимый признак сходимости
не выполняется и ряд расходится. В
предельной форме эта теорема выглядит
так: Теорема.
Пусть существует невозможно.
Т.о. необходимый признак сходимости
не выполняется и ряд расходится. В
предельной форме эта теорема выглядит
так: Теорема.
Пусть существует
 .
Тогда если q<1
– ряд сходится, q>1
– ряд расходится, q=1
– признак неприменим.
Доказательство.
Пусть
q<1 .
Выберем .
Тогда если q<1
– ряд сходится, q>1
– ряд расходится, q=1
– признак неприменим.
Доказательство.
Пусть
q<1 .
Выберем
 так,
чтобы так,
чтобы
 (т.е. (т.е.
 ).
Тогда при ).
Тогда при
 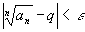 ,
т.е. ,
т.е.
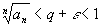 .
Применяя предыдущую теорему получаем,
что ряд сходится.
Если же q>1,
то выберем .
Применяя предыдущую теорему получаем,
что ряд сходится.
Если же q>1,
то выберем
 так,
что так,
что
 (т.е. (т.е.
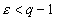 ).
Тогда ).
Тогда
 .
Вновь по предыдущей теореме ряд
расходится. Теорема.
(Признак сходимости Даламбера). Пусть
при всех n>=n0 .
Вновь по предыдущей теореме ряд
расходится. Теорема.
(Признак сходимости Даламбера). Пусть
при всех n>=n0
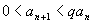 ,
где q<1.
Тогда ряд сходится. Если же при
n>=n0,an+1
>=an
то ряд
расходится.
Доказательство.
Из условий теоремы следует ,
где q<1.
Тогда ряд сходится. Если же при
n>=n0,an+1
>=an
то ряд
расходится.
Доказательство.
Из условий теоремы следует
  .
Иными словами, .
Иными словами,
 и
по первой теореме сравнения ряд
сходится. Если an+1
>=an,
то и
по первой теореме сравнения ряд
сходится. Если an+1
>=an,
то
 при при
 и
ряд расходится. В предельной форме
этот признак выглядит так: Теорема.
Если существует и
ряд расходится. В предельной форме
этот признак выглядит так: Теорема.
Если существует
 ,
то при q<1
ряд сходится, при q>1
- расходится, а при q=1признак
неприменим.
Доказательство.
При q<1
выбираем ,
то при q<1
ряд сходится, при q>1
- расходится, а при q=1признак
неприменим.
Доказательство.
При q<1
выбираем
 так,
чтобы так,
чтобы
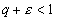 .
Пусть n0
выбрано
так, чтобы при n>=n0 .
Пусть n0
выбрано
так, чтобы при n>=n0 ,
т.е. ,
т.е.
 и и
 , ,
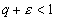 .
По предыдущей теореме ряд сходится.
Если же q>1,
то выберем .
По предыдущей теореме ряд сходится.
Если же q>1,
то выберем
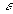 так,
что так,
что
 .
Тогда при .
Тогда при
 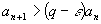 и ряд расходится. Теорема.
(признак Гаусса). Пусть
и ряд расходится. Теорема.
(признак Гаусса). Пусть
 и и
 , ,
 .
В применении
к ряду .
В применении
к ряду
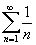 она
дает: она
дает:
 , ,
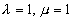 -
ряд расходится. Для ряда -
ряд расходится. Для ряда
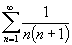 имеем: имеем:
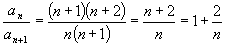 , ,
 -
ряд сходится. -
ряд сходится.
|

