Программирование / си++ / ЛЕКЦИИ АСУ-03 за 1й курс / II cemecTP / Шпоры по матану / 16-20 / 41-45 / 41-45

(41)Криволинейные координаты на плоскости. Вычисление 2-го интеграла в полярных координатах.

Для упр. вычисл. 2-го инт-ла часто применяют метод подстановки, т.е. вводят новые переменные под знаком двойного интеграла.

Определим преобразование независимых перем. х и у (замену перем.) как x=(u,v) и (u,v).

Если ф-ии имеют в некотор. области D* плоскости Ouv непрерывные частные пр-е первого порядка и отличный от нуля определитель I(u,v)=,(*)

а ф-я f(x,y) непрерывна в области D, то справедлива формула замены ппеременных в 2-м инт-ле:

J_DJf(x,y)dxdy=J_D*Jf( (u;v);(u,v))|I(u,v)|dudv.(^)

Функциональный определитель назыв. опр. Якоби или якобианом.

Рассм. част. случ. замены перем. , часто используемый при вычислении 2-го ин-ла, а имеенно замену декартовых коорд х и у на полярные коорд r и .

В качестве u и v возьмем полярные коорд r и . Они связаны с декартовыми коорд формулами x=rcos, y=rsin.

Правые части в неравенствах – непрерывно дифференцируемые ф-и. Якобиан преобразования определяется из (*) как

I(r, )=== r.

Формула замены переменных (^) принимает вид :

J_DJf(x;y)dxdy=J_D*Jf(rcos; rsin)*r*dr*d,(!)

где D* - область в полярной системе коорд, соотвующая области D в декартовой сис-ме коорд.

Для вычисления 2-го инт-ла в полярн коорд применяют то же правило сведения его к двукратному инт-лу. Так, если область D* имеет вид, изобр на рис (ограничена лучами = и =, где <, и кривые r=r₁() и r=r₂() , где r₁() <= r₂(), т.е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более 2-х раз), то правую часть формулы (!) можно записать в виде

J_D*Jr*f(rcos; rsin)drd=J^_dJ ^r2()_r1()r*f(r rcos; rsin)dr).

Внутренний интеграл берется при постоянном .

(42)Вычисление криволинейных и поверхностных интегралов 1-го порядка

Вычислению криволинейного инт-ла 1 порядка может быть сведено к вычислению определенного инт-ла.

Правила вычисления криволинейного инт-ла 1 рода в случаях когда кривая L задана параметрическим, полярным и явным образом.

ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ

Если кривая АВ задана параметрическими ур-ми x=x(t), y=y(t), t[;], где x(t) и y(t) – непрерывно дифференцируемые функции параметра t, причем точке А соответствует t=, точке B – значение t=, то

J_ABf(x;y)dl=J^_f(x(t);y(t))*^2I_t+y^2I_tdt

Аналогичная формула имеет место для криволинейного инт-ла от ф-и f(x;y;z) по пространственной кривой АВ задаваемой ур-ми x=x(t), y=y(t), z=z(t), <=t<=:

J_ABf(x;y;z)dl=J^_f(x(t);y(t);z(t)) ^2I_t+y^2I_t+z^2I_tdt.

ЯВНОЕ ПРЕДСТАВЛЕНИЕ

Если кривая АВ задана ур-ем y=(x), x[;], где (x) – непрерывно дифференцируемая ф=я, то

J_ABf(x;y)dl=J^_f(x; (x))1+ y^2I_tdx.(1)

Подынтегральное выражение в правой части фор-лы (1) получается заменой в левой части y=(x) и

dl= 1+y^2I_x*dx (дифференциал дуги кривой)

Полярное представление

Если плоская кривая L задана ур-м r=r(),<=<= в полярных координатах, то dl=r²+r^I_²*d.

Подчеркнем, что нижний предел определенного инт-ла должен быть меньше верхнего.

Вычисление поверхностного интеграла 1 рода.

Вычисление поверхностного интеграла 1 рода сводится к вычислению двойного инт-ла по области D – проекции поверхности S на плоскость Oxy.

Разобьем повнрхность S на часть S_i, i – . Обозначим через _i gпроекцию S_i на плоскость Oxy. При этом область D окажется разбитой на n частей ₁ , ₂, … , _n. Возьмем _I произвольную точку P_i(x_i;y_i) и восстановим перпендикуляр к плоскости Oxy до пересечения с поверхностью с поверхностью S. Получим точку M_i(x_i;y_i;z_i) на поверхности S_i. Проведем в точке M_i касательную плоскость и рассмотрим ту ее часть T_i , которая на плоскость Oxy проектируется в область _I(см. рис.). Площади эл-х часлей S_i, T_i, _i обозначим как S_i, T_i, _I соответственно. Будем приближенно считать, что T_iS_i.

Обозначив через _I острый угол м/ду осью Oz и нормалью к поверхности в этой точке M_i, получаем:T_icos_I=_i (*) (область _i есть проекция T_i на плоскость Oxy).

Если поверхность S задана ур-м z=z(x,y), то как известно ур-е касательной плоскости в точке M_i есть

z^I_x(x_i;y_i)(x-x_i)+z^I_y(x_i;y_i)(y-y_i)-(z-z_i) =0

где z^I_x(x_i;y_i), z^I_y(x_i;y_i) – 1 – координаты нормального вектора к плоскости. Острый угол _I есть угол м/ду векторами =(0;0;1) и =(- z^I_x(x_i;y_i);- z^I_y(x_i;y_i);1).Следовательно,

cos_I==(1+ z^I_x²(x_i;y_i)+z^I_y²(x_i;y_i))(выражение под корнем)

Равенство (*) принимает вид

T_i=1+ z^I_x²(x_i;y_i)+z^I_y²(x_i;y_i) _i

В правой части формулы J_sJf(x;y;z)ds=_nlim_0ⁿ_i=1f(x_i;y_i;z_i) S_i

Заменим S_i на полученное выражение для T_i, а z_i заменим на z(x_i;y_i). Поэтому, переходя к пределу при стремлении к нулю наибольшего диаметра S_i (а следовательно и _i) получаем формулу

J_SJf(x;y;z)ds=J_DJf(x;y;z(x;y)) 1+ z^I_x²+z^I_y²dxdy

Выражающую интеграл по поверхности S через двойной инт-л по проекции S на плоскость Oxy.

Отметом, что если поверхность S задана ур-м вида y=y(x;z) или x=x(y;z), то аналогично получим

J_SJf(x;y;z)ds=J_D1Jf(x;y(x;z);z) 1+ y^I_x²+y^I_z²dxdz и

J_SJf(x;y;z)ds=J_D2Jf(x(y;z);y;z) 1+ x^I_y²+x^I_z²dxdz

Где D1 и D2 – проекции поверхности S на координатные плоскости Oxz и Oyz соответственно.

(43)Цилиндрические и сферические координаты в пространстве, вычисление тройных интегралов в них.

При вычислении 3-го интеграла, как и двойного часто применяют метод подстановки, т.е. совершается преобразование переменных.

Пусть совершена подстановка x=(u,v,w),y=(u,v,w), z=(u,v,w).

Если эти функции имеют в некоторой области V* пространства Оuvw непрерывные частные производные и отличные от нуля определитель I(u,v,w)=

То справедлива формула замены переменных в 3-м интеграле:

J_vJJ f(x,y,z)dxdydz=

J_v*JJ f((u,v,w);(u,v,w);(u,v,w))|I(u,v,w)|dudvdw.

Здесь I(u,v,w) – определитель Якоби, или якобиан преобразования.

Для вычисления 3-го интеграла часто используют так называемые цилиндрические координаты.

Положение точки M(x,y,z) в пространстве Oxyz можно определить заданием 3 чисел r, , z, где r – длина радиус-вектора проекции точки М на плоскость Oxy,  - угол, образованный этим радиусом-вектором с осью Ох, z – аппликата точки М

Эти 3 числа (r, ,z) называются цилиндрическими координатами точки М.

Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:

x=r*cos, y=r*sin, z=z

(r>=0, [0;2],zR).

Возьмем в качестве u,v,w цилиндрические координаты r, , z и вычислим якобиан преобразования:

I=(r, ,z)= ==

=r>=0.

Формула замены переменных принимает вид

J_vJJf(x,y,z)dxdydz=J_v*JJf(rcos;rsin;z)rdrddz.

Таким образом, вычисление 3-го интеграла приводится к интегрированию по r,  и по z аналогично тому, как это делается в декартовых координатах.

Замечание: К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.

(44)Приложения интегралов по фигурам

Двойные интегралы

Объем цилиндрического тела V=J_DJ f(x;y)dxdy,

Где z=f(x;y) – ур-е поверхности, ограничивающей тело сверху.

Площадь плоской фигуры : Если положить в формуле

V=J_DJf(x;y)dxdy f(x;y)=1, то цилиндрическое тело превратится в прямой цилиндр с высотой H=1. Объем такого цилиндра, как известно численно равен плошади S основания D . Получаем формулу для вычисления площади площади S области D: S=J_DJdxdy, или, в полярных координатах, S=J_DJrdrd.

Масса плоской фигуры.

Как уже показано масса плоской пластинки D с переменной плоскостью =(x;y) находится по формуле

m=J_DJ(x;y)dxdy.

Статические моменты и координаты центра тяжести плоской фигуры.

Статические моменты фигуры D относительно осей Ox и Oy могут быть вычислены по формулам S=JJ

(45)Криволинейные интегралы 2-го рода, свойства, вычисление.

Обобщим понятие определенного интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащей в плоскости.

Интегралы такого рода называются криволинейными. Они имеют широкое применение в различных разделах математики.

Различают 2 типа криволинейных интегралов: криволинейные интегралы 1-го и 2-го рода.

Определение криволинейного интеграла 2-го рода:

Пусть на кривой АВ определены 2 ограниченные функции Р(х,у) и Q(х,у). Разобьем кривую АВ на n частей точками А=М₀, М₁, …, М_i-1, М_i, …,M_n=B. Обозначим через x_i и y_i проекции вектора М_{i –1}М_i на оси координат на каждой частичной дуге М_{i –1}М_i возьмем произвольную точку М_i^* и составим интегральную сумму для функции Р(х,у) [ Q(х,у)]: ⁿ_i=1P(M^*_i) x_i[ⁿ_i=1Q(M^*_i) y_i] (*)

Определение. Если интегральная (*) сумма при 0 (=мах_I<=i<=n{l_i}, l_i - длина дуги М_{i –1}М_i) имеем предел, равный I, то этот предел называется криволинейным интегралом второго рода от функции Р(х,у) [ Q(х,у)] по кривой АВ и обозначается cимволом J_ABP(x,y)dx[J_ABQ(x,y)dy] .

Сумму J_ABP(x,y)dx+J_ABQ(x,y)dy

Называют общим криволинейным интегралом 2-го рода и обозначают символом J_ABP(x,y)dx+Q(x,y)dy

Криволинейные интегралы 2-го рода, как и интегралы первого рода, легко сводятся к определенным интегралам.

Д-но, пусть кривая АВ задана параметрически уравнениями x=(t), y=(t), <=t<=, где (t) и (t) – непрерывные вместе со своими производными ^I(t) и ^I(t) функции, причем точке А кривой соответствует значение t=, точке В – значение t=, ^I2(t)+ ^I2(t) 0. Пусть функция P(x,y) и Q(x,y) непрерывны вдоль кривой АВ. Тогда справедливы следующие формулы:

J_ABP(x,y)dx=J^_P[(t),(t)] ^I(t)dt;

J_ABQ(x,y)dy=J^_Q[(t) ),(t)] )^I(t)dt;(*)

J_ABP(x,y)dx+Q(x,y)dy=J^_{P[(t),(t)] ^I(t)+Q[(t), (t)] ^I(t)}dt

Сводящие криволинейные интегралы к определенным интегралам.

Вычисление: Криволинейные инт-лы 2 рода вычисл сведением их к определенным инт-м по формулам (*).

В частности если кривая АВ задана ур-ем вида y=y(x), a<=x<=b, где y(x) – непрерывно дифференцируемая ф-я то принимая х за параметр (t=x), из формул (*) получаем

J_ABP(x,y)dx=J^_P(x,y(x)|dx, J_ABQ(x,y)dy=J^_Q|x,y(x)|y^I(x)dx,

J_ABP(x,y)dx+Q(x,y)dy=J^_{P|x,y(x)|+Q|x,y(x)|y^I(x)}dx.

Аналогичные формулы имеют место, если кривая АВ задана ур-м вида x=x(y).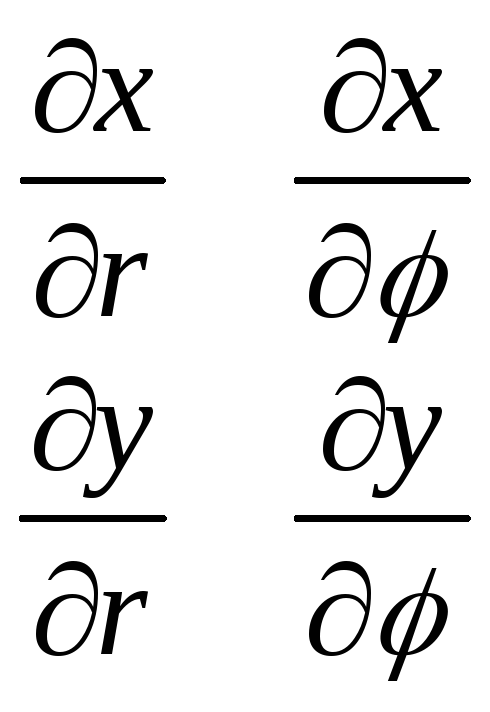
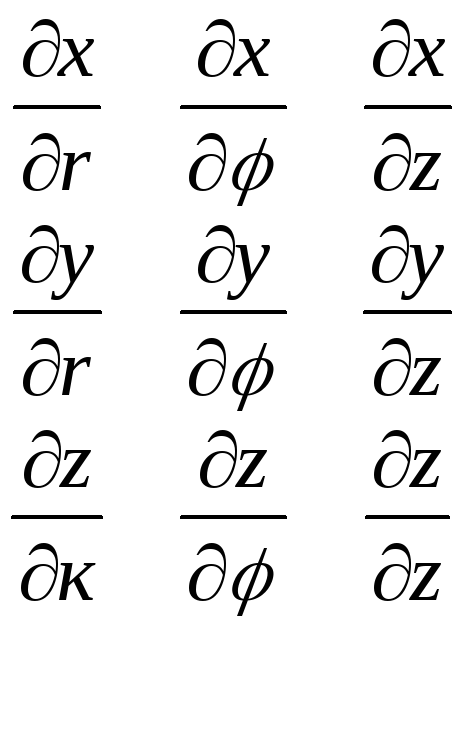