Программирование / си++ / ЛЕКЦИИ АСУ-03 за 1й курс / II cemecTP / Шпоры по матану / 6-10 / МОИ ШПОРЫ

(06) Вычисление объёма тел с помощью определенного интеграла

Пусть тело V расположено в пространстве между плоскостями x = a и x = b, и для известна площадь его поперечного сечения S = S(x). Требуется определить объём этого тела.

Рассечём это тело плоскостями x = x0 = a, x = x1, x = x 2, …, x = xi-1, x = xi, …, x = x n-1, x = xn = b на n слоёв (a = x0< x1 < < x2< …< xn-1 < xn = b), на каждом из отрезков [xi-1, xi] возьмём произвольную точку будем считать, что объём слоя, заключенного между плоскостями x = xi-1 и x = xi приближённо равен объёму цилиндрика с площадью основания 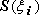и высотой Сумма объёмов - объём ступенчатой фигуры стремится к искомому объёму V, поэтому

Если объём V получается в результате вращения кривой y = f(x), , вокруг оси Ox, то,

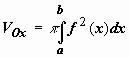
(07) Вычисление площади поверхности вращения с помощью определённого интеграла

Площадь поверхности вращения, образующейся при вращении вокруг оси Ox дифференцируемой кривой, определяется по формулам (в зависимости от способа задания кривой)

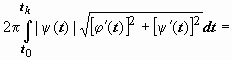
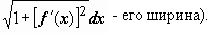
1. Формула Ньютона-Лейбница вычисления определённого интеграла.

2. Замена переменной в определённом интеграле

3. Интегрирование по частям в определённом интеграле

4. Приложение определённого интеграла к вычислению площади в декартовых полярных координатах, при параметрическом задании границы криволинейной трапеции.

5. Вычисление дуги плоской кривой при разных способах задания

6. Вычисление объёма тел с помощью опре6делённого интеграла

7. Вычисление площади поверхности вращения с помощью определённого интеграла

8. Физические приложения определённого интеграла

9. Не собственные интегралы 1-го рода, признаки их сходимости

10. Не собственные интегралы 2-го рода, признаки их сходимости

11. Точечные множества на плоскости и в пространстве; открытые, замкнутые и связанные множества.

12. Понятие ф-ии 2 –х и нескольких переменных, способы и задания.

13. Понятия предела последовательности в Rⁿ и предела функции и переменных

14. Основные свойства пределов последовательностей и функций в Rⁿ

15. Непрерывность функций и переменных. Свойства функций и переменных, непрерывных в точке, в открытой области и замкнутом множестве .

16. Частные производные функции нескольких переменных 1-го и высших порядков. Теорема ос мешанных производных.

17. Дифференцируемость и дифференциал функции нескольких переменных. Необходимые и достаточные условия дифференцируемости.

18. Дифференцирование сложных функций нескольких переменных. Инвариантность формы дифференциала 1-го порядка и не инвариантность формы дифференциала 2-го порядка.

19. Теорема существования и правило дифференцирования неявных функций двух и нескольких переменных

20. Производная функции нескольких переменных по направлению, её вычисление

21. Градиент функции нескольких переменных, его свойства.

22. Касательная плоскость и нормаль к поверхности

23. Геометрический смысл дифференциала функции 2-х переменных

24. Экстремум функции нескольких переменных. Необходимые условия экстремума.

25. Достаточное условие экстремума функции нескольких переменных

26. Наибольшее и наименьшее значение функции нескольких переменных в замкнутой области.

27. Условный экстремум функции нескольких переменных . Мету. Множителей Лагранжа

28. Понятие решения, частного и общего решения дифференциального уравнения 1-го порядка. Теорема существования и единственности решения задачи Коши, мету изокмен.

29. Уравнения с разделяющимися переменными и однородные 1-го порядка , методы их решения.

30. Линейные уравнения и уравнения Бернулли, методы их решения.

31. Понятия связанные с уравнениями 2-го и высших порядков, их решения методом понижения порядка.

32. Общая теория линейных дифференциальных уравнений 2-го порядка и высших порядков.

33. Теорема о структуре общих решений однородных и неоднородных уравнений 2-го и высших порядков.

34. Линейные однородные и диф уравнения с постоянными коэффициентами , их фундаментальные системы решений

35. Решение неоднородных линейных уравнений с постоянными коэффициентами и медиальной кривой частью.

36. Метод вариации произвольных постоянных для решения линейных неоднородных уравнений.

37. Исследование колебаний механических систем или тока в замкнутой цепи. Явление резонанса.

38. Понятие устойчивости и асимптотической устойчивости по Ляпунову для диф. Уравнения 1-го порядка.

39. Понятия и свойства интегралов по фигурам.

40. Вычисление двойных и тройных интегралов в декартовых координатах

41. Криволинейные координаты на плоскости. Вычисление двойных интегралов в полярных координатах.

42. Вычисление криволинейных и поверхностных интегралов 1-го порядка.

43. Цилиндрические и сферические координаты в пространстве, вычисление тройных интегралов в них.

44. Приложение интегралов по фигурам.

45. Криволинейные интегралы 2-го рода, свойства, вычисление.

46. Поверхностные интегралы 2-го рода, свойства, вычисление

47. Формула Грина

48. Формулы Остроградского-Гауса и Стасса. Их приложения.

49. Понятие и необходимый признак сходимости числового ряда, их простейшие свойства

50. Достаточные признаки сравнения и Даламбера сходимости знакоположительных рядов.

51. Достаточный признак Коши (радикальной и интегральной сходимости знакоположительных рядов).

52. Знакочередующие ряды, признак Лебница.

53. Знакопеременные ряды, абсолютная и условная сходимость, оценка остатка.

54. Функциональные ряды, их сходимость, понятие равномерной сходимости. Свойства равномерно сходящихся рядов.

55. Степенные ряды. Теорема Абеля, интервал сходимости.

56. Ряды Тейлора , разложение элементарных функций в ряд Тейлора, приложения рядов Тейлора.

57. Ортогональные системы функций, сходимость в среднем, понятие ряда Фурье.

58. Тригонометрические ряды Фурье.

59. Условие сходимости рядов Фурье.

60. Понятие интеграла и преобразований Фурье.

(09) Не собственные интегралы 1-го рода, признаки их сходимости

Пусть функция f(x) определена на полуоси и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла называется несобственным интегралом функции f(x) от a до и обозначается

Если этот предел существует и конечен, интеграл называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.

Если сходится интеграл 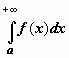, а интеграл расходится, то интеграл называется сходящимся условно.

(10) Не собственные интегралы 2-го рода, признаки их сходимости

Пусть функция f(x) определена на полуинтервале (a, b], интегрируема по любому отрезку , и имеет бесконечный предел при Несобственным интегралом от f(x) по отрезку [a, b] называется предел Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.

Если для функции f(x) на полуинтервале (a, b] существует первообразная F(x), то

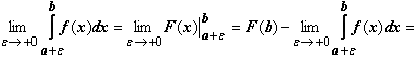
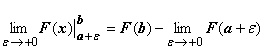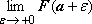и сходимость интеграла определяется наличием или отсутствием конечного предела Признаки сравнения для неотрицательных функций. Как и для несобственных интегралов первого рода, для интегралов второго рода вводится понятие абсолютной сходимости, позволяющее в ряде случаев свести исследование сходимости интегралов от произвольных функций к исследованию сходимости интегралов от неотрицательных функции, и рассматриваются признаки сравнения для таких интегралов.