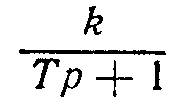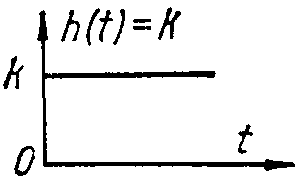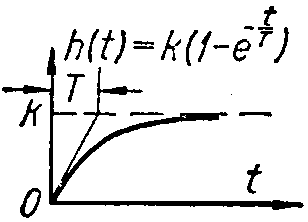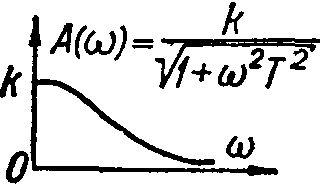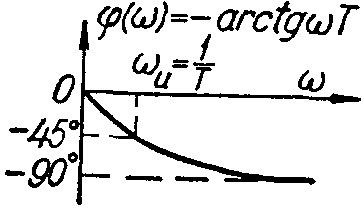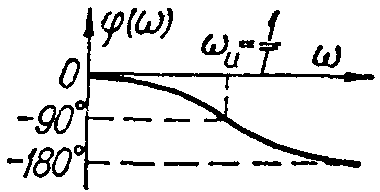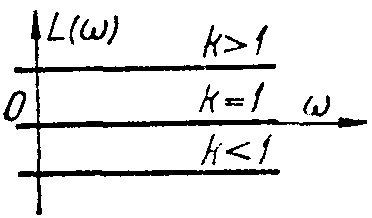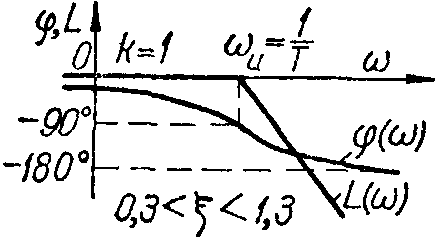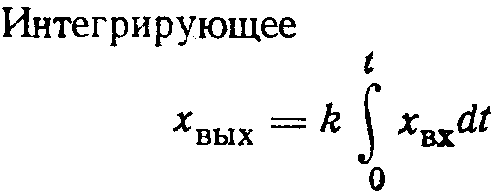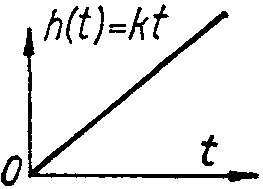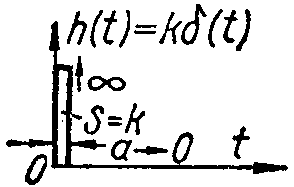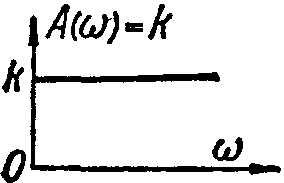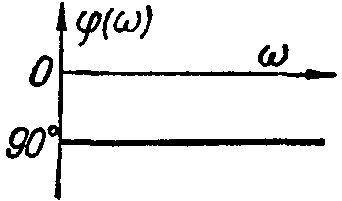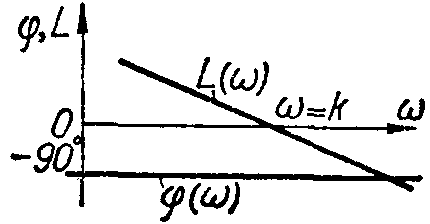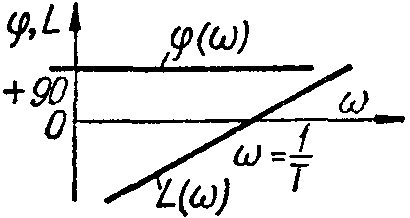АСУ ТП / асу на 192.168.2.74 / ИДЗ

Федеральное агентство по образованию РФ

Обнинский государственный технический университет атомной энергетики

Физико-энергетический факультет

Кафедра ОиЭ ЯЭУ

Индивидуальное домашнее задание по курсу

«АСУ АЭС»

Определение и критерии устойчивости автоматических систем регулирования

Выполнил: студент гр. Э-1-04

Шведов В.А.

Преподаватель: Зорин М.А.

Обнинск, 2008 г.

1. Устойчивость линейных САУ.

   1. Любая САУ характеризуется переходным процессом, который возникает в ней при нарушении состояния равновесия вследствие какого-либо воздействия. Переходный процесс х(t) зависит как от свойств системы, так и от вида возмущающего воздействия. В переходном процессе различают две составляющие:

,

первая из них выражает вынужденные движения, определяемые возмущающим воздействием и свойствами системы; вторая — свободные движения системы, определяемые начальными условиями и свойствами самой системы.

Основной динамической характеристикой САУ является ее устойчивость. Под устойчивостью понимается свойство системы возвращаться к состоянию установившегося равновесия после устранения возмущения, которое вывело ее из этого состояния.

Невозмущенное движение будет устойчивым, если для всякого положительного числа , как бы мало оно ни было, можно подобрать другое число , зависящее от , такое, что для всех возмущенных движений, для которых в начальный момент

, (1)

при всех выполняется неравенство

. (2)

Из уравнения (2) видно, что при оценке устойчивости отклонения не должны превосходить некоторой достаточно малой величины , а из уравнения (1) – что начальные условия при этом отличны от нуля, но не превосходят некоторого значения , зависящего от выбранного значения .

Если выполняется условие , то система называется неограниченно устойчивой, то есть она будет устойчивой при любых начальных отклонениях. Если система устойчива при и неустойчива при , то она является устойчивой «в малом» и неустойчивой «в большом» (при ). Если выполняется условие , то система называется асимптотически устойчивой.

Все реальные САУ являются нелинейными. Линейные характеристики звеньев и линейные дифференциальные уравнения можно получить путем линеаризации реальных характеристик и уравнений. Обоснование законности линеаризации нелинейных САУ содержится в теоремах А.М.Ляпунова. Суть этих теорем заключается в следующем:

1. Если линеаризованная система устойчива, то устойчива исходная нелинейная система.

2. Если линеаризованная система неустойчива, то неустойчива и исходная нелинейная система.

3. Если линеаризованная система находится на границе устойчивости, то для определения устойчивости исходной нелинейной системы необходимо произвести дополнительные исследования по исходным нелинейным уравнениям системы.

Эти теоремы справедливы для исследования устойчивости САУ в малом, а также по отношению к несильно выраженным нелинейностям. К нелинейностям релейного типа эти теоремы неприменимы.

2. Если для разомкнутой САУ известна передаточная функция 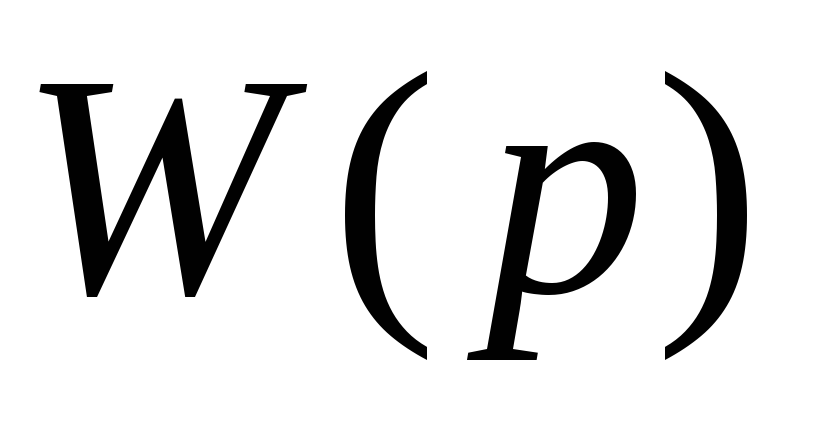, то для замкнутой системы передаточная функция будет иметь вид

,

откуда, приравнивая знаменатель к нулю, получим характеристическое уравнение системы:

.

Для устойчивости линейной САУ необходимо и достаточно, чтобы вещественные корни и вещественные части комплексных сопряженных корней характеристического уравнения были отрицательными. Определение устойчивости САУ путем вычисления корней характеристического уравнения не всегда приемлемо из-за высокого порядка решаемых алгебраических уравнений. Поэтому на практике используют разные критерии устойчивости, позволяющие без вычисления корней судить об устойчивости исследуемой системы. Различают алгебраические и частотные критерии оценки устойчивости.

Алгебраические критерии устойчивости основаны на исследовании зависимости между коэффициентами характеристического уравнения и характером распределения корней этого уравнения в комплексной плоскости. Наиболее распространенным является критерий Гурвица (1895 г.). Формулировка: система с характеристическим уравнением

будет устойчивой, если определитель Гурвица и все его диагональные миноры положительны, т.е. если ; ; …; . Определитель Гурвица имеет вид

Частотные критерии устойчивости основаны на изучении связи между формой частотной характеристики САУ и характером распределения корней характеристического уравнения. В 1938 г. советский ученый А.В.Михайлов предложил графический критерий устойчивости. Если характеристическое уравнение замкнутой САУ имеет вид

,

то, представив левую часть этого уравнения в виде функции от р

и заменив p на , получим уравнение комплексного вектора

,

конец которого при изменении угловой частоты колебаний от нуля до бесконечности опишет на комплексной плоскости некоторую кривую – годограф, эта кривая называется кривой Михайлова. Система n-го порядка будет устойчивой, если годограф , начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно n квадрантов.

Критерий Найквиста. Чтобы замкнутая САУ была устойчивой, необходимо и достаточно соблюдение следующих условий:

1. при устойчивой разомкнутой САУ (или находящейся на границе устойчивости) АФЧХ при изменении от 0 до не должна охватывать точку с координатами -1, j0;

2. при неустойчивой разомкнутой САУ АФЧХ при изменении от до должна охватывать точку -1, j0 столько раз, сколько корней характеристического уравнения разомкнутой системы лежит справа от мнимой оси плоскости корней.

Логарифмический критерий устойчивости. Если разомкнутая САУ устойчива, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы во всех областях положительных ЛАХ разность между числом положительных и отрицательных переходов фазовой характеристики через линию - равнялась нулю.

3. Во многих случаях при проектировании систем, а также при их настройке и наладке бывает необходимо знать все возможные значения некоторых параметров называемых варьируемыми, при которых система устойчива. Эта задача решается путем выделения области устойчивости в пространстве варьируемых параметров. Метод выделения области устойчивости принято называть методом D-разбиения.

Возьмем характеристическое уравнение замкнутой САУ третьей степени, имеющее вид

.

Уравнение имеет 3 корня: , и , которые являются непрерывными функциями коэффициентов , , и . Приходим к системе:

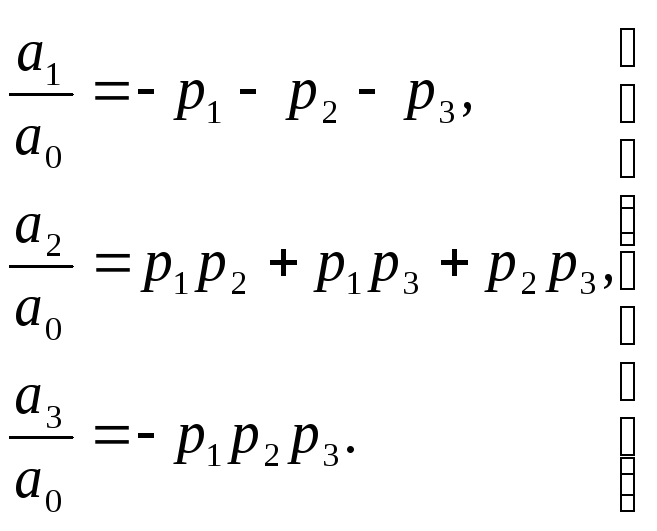
Система уравнений выражает коэффициенты характери­стического уравнения через его корни. При бесконечно малом изменении корней коэффициенты получают бесконечно малые приращения и наоборот. То есть корни уравнения явля­ются непрерывными функциями коэффициентов уравнения

; ; .

Коэффициенты уравнения , , и можно рассмат­ривать как координаты некоторой, так называемой фигуративной, точки А в четырехмерном пространстве коэффициентов. Каждому положению точки А в этом пространстве соответствует опреде­ленная совокупность численных значений координат (т. е. коэф­фициентов уравнения), а следовательно, и определенное распре­деление корней уравнения на комплексной плоскости p.

Из этих рассуждений видно, что пространство коэффициентов можно разделить на области так, что всем точкам, принадлежа­щим одной и той же области, будет соответствовать одно и то же количество корней, лежащих слева от мнимой оси. Для характе­ристического уравнения третьей степени можно найти области таких значений коэффициентов уравнения, которым соответству­ют 0, 1, 2 или 3 левых корня. Такое разбиение пространства коэффициентов называется D-разбиением, а граница этих областей (поверхность в многомерном пространстве), заданная аналитиче­ски или графически, называется границей D-разбиения.

II. Типовые динамические звенья САУ.

Передаточной функцией в форме преобразований Лапласа называется отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях. Если передаточная функция превращается в коэффициент усиления.

При синтезе и анализе САУ её расчленяют на типовые звенья, которые различаются динамическими свойствами. Для оценки динамических свойств системы используются временные и частотные характеристики.

К временным характеристикам звеньев относятся их переходные функции:

а) переходная функция;

б) импульсная переходная функция (функция веса).

Переходная функция звена определяет его реакцию на единичную ступенчатую функцию (воздействие) и характеризует переход звена от одного состояния к другому.

Импульсная переходная характеристика является реакцией звена на единичную импульсную входную функцию . Реакция на единичную импульсную функцию называется функцией веса . Связь между переходной и весовой функциями .

Частотные характеристики:

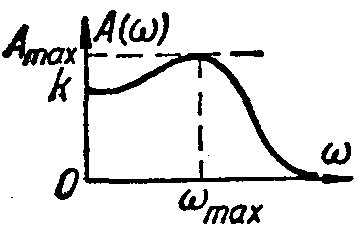
а) АЧХ (амплитудно-частотная);

б) ФЧХ (фазово-частотная);

в) АФЧХ (амплитудная фазово-частотная).

Частотные характеристики характеризуют реакцию звена на гармонический входной сигнал . На выходе будет функция , отличающаяся от входной по амплитуде и по фазе.

За типовые звенья целесообразно принять такие, которые могут служить для построения любых других звеньев, встречающихся на практике. Обычно за основу принимают звено, принимающее 1 степень свободы. Математические процессы в таком звене описываются дифференциальным уравнением 2-го порядка

.

Если принять это уравнение за переходное, то легко вывести уравнения различных типовых звеньев. Типовые звенья являются звеньями направленного действия, сигналы передаются в одном направлении с входа на выход.

Типовые звенья:

1. пропорциональное (усилительное);

2. апериодическое (инерционное);

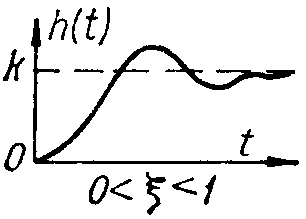
3. колебательное;

4. дифференцирующее;

5. интегрирующее;

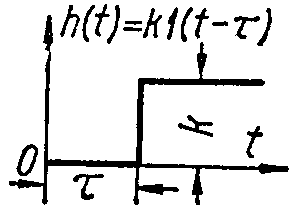
6. запаздывающее.

Характеристики типовых звеньев автоматических систем.

Тип и уравнение звена
Передаточная функция
Переходная функция
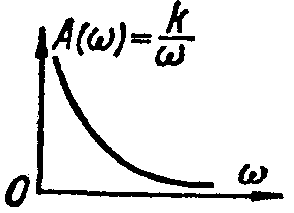
АЧХ
ФЧХ
ЛЧХ

Тип и уравнение звена
Передаточная функция
Переходная функция
АЧХ
ФЧХ
ЛЧХ