1 курс / Линейная алгебра / Линейная алгебра (теория)

1. Векторы. Свойства вектора. Операции над векторами.

Вектор – направленный отрезок, имеющий начальную и конечную точки. Длиной (или модулем) вектора называется число, равное длине направленного отрезка. Вектор, длина которого равна единице, называется единичным вектором, или ортом. Вектор, начало и конец которого совпадают, называется нулевым. Векторы, лежащие на параллельных прямых, называются коллинеарными.

N-мерный вектор – упорядоченная совокупность (х₁, х₂, …, х_n) n вещественных чисел. Числа х_i (i = 1, 2, …,n) называются компонентами (или координатами) вектора.

Свойства векторов:

1. Равные векторы в единой системе координат имеют равные координаты.

2. Координаты коллинеарных векторов пропорциональны:

3. Квадрат длины вектора равен сумме квадратов его координат.

4. При сложении векторов соответствующие координаты векторов складываются.

5. Скалярное произведение двух векторов равно сумме произведений их соответствующих координат или произведению их длин на косинус угла между ними:

Операции над векторами:

1. Суммой векторов a и b называется вектор с = a + b, начало которого совпадает с началом вектора а, а конец – с концом вектора b. Этот способ построения называется правилом треугольника.

2. Разностью секторов а и b называется вектор с = а + (-1)b = a – b.

3. Произведение вектора 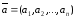на число α называется вектор b, имеющий длину . Направление вектора b совпадает с направлением вектора а, если , и противоположно по направлению, если .

Свойства операций:

1. а + b = b + a

2. a + (b + c) = (a + b) + c

3. a + 0 = a

4. α(a + b) = αa + αb

5. a*0 = 0

2. Линейное пространство. Свойства линейного пространства. Подпространство линейного пространства.

Множество W элементов х, у, z, называется линейным пространством, если по некоторому правилу:

1. Любым двум элементам х и у из W поставлен в соответствие элемент из W, обозначаемый х + у и называемый суммой элементов х и у.

2. Любому элементу х из W и каждому числу λ поставлен в соответствие элемент из W, обозначаемый λ*x и называемый произведением числа λ на элемент х, причём справедливы следующие аксиомы:

1. х + у = у + х

2. (х + у) + z = x + (y + z)

3. λ*(x + y) = λx + λy

4. (λ + μ)x = λx + μx

5. λ*(μ*x) = (λ*μ)*x

6. 1*x = x

7. Существует нулевой элемент О такой, что х + О = х для любого х € W

8. Для каждого элемента х существует противоположный элемент –х такой, что х + (-х) = О

Линейное пространство называется пустым, если оно состоит из нулевого элемента.

Свойства:

1. Любое линейное пространство имеет только один нулевой вектор.

2. Каждый вектор линейного пространства имеет только один противоположнгый вектор.

3. Если вектор (-х) противоположен вектору х, то вектор х противоположен вектору (-х).

4. Для любых векторов а и b уравнение а + х = b имеет решение, и притом единственное.

5. Произведение произвольного элемента линейного пространства на число 0 равно нулевому вектору: х*0 = 0

6. Вектор, противоположный данному вектору х, равен произведению х на -1.

7. Произведение нулевого вектора на любое число есть нулевой вектор.

Линейное подпространство или векторное подпространство ― непустое подмножество К линейного пространства W такое, что K само является линейным пространством по отношению к определенным в W действиям сложения и умножения на скаляр.

Свойства подпространств:

1. Пересечение любого семейства подпространств — подпространство;

2. Сумма конечного семейства подпространств — подпространство.

3. Линейная зависимость и линейная независимость векторов. Свойства линейно зависимых векторов. Линейная оболочка векторов.

Набор векторов а₁, а₂, …, а_N называется системой векторов.

Система векторов а₁, а₂, …, а_N является линейно зависимой, если существуют такие числа λ₁, λ₂, …, λ_n, при которых а₁*λ₁ + а₂*λ₂ + … + a_n*λ_n = 0

Cистема векторов является линейно независимой, если равенство возможно только при λ₁ = λ₂ = … = λ_n = 0.

Свойства линейно зависимых векторов:

1. Если в систему векторов входит нулевой вектор, то она линейно зависима.

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора, то она линейно зависима.

4. Система из n > 1 векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

Линейная оболочка V(X) подмножества X линейного пространства V — пересечение всех подпространств V, содержащих X.

4. Размерность линейного пространства. Базис и ранг системы векторов. Разложение вектора по системе векторов. Преобразование координат при замене базиса.

Число k называется размерностью линейного пространства L, если в L существует система из k линейно независимых векторов, а любая система из k+1 вектора — линейно зависима.

Рангом системы векторов называется максимальное число линейно независимых векторов системы. Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.

Пусть дана система n-мерных векторов А₁, А₂, …, А_n. Выберем n произвольных чисел k₁, k₂, …, k_n. Заметим, что чисел ровно столько, сколько векторов в системе. Вектор k₁A₁ + k₂A₂ + … +k_nA_n называется линейной комбинацией векторов А₁, А₂, …, А_n с коэффициентами k₁, k₂, …, k_n.

Пусть наряду с векторами А₁, А₂, …, А_n дан m-мерный вектор B. Будем говорить, что вектор В линейно выражается через векторы А₁, А₂, …, А_n, если он равен некоторой линейной комбинации векторов А₁, А₂, …, А_n, т. е. найдётся такой набор чисел l₁, l₂, ... , l_n, что В = l₁A₁ + l₂A₂+…+l_nA_n.

Вектор В разлагается по векторам А₁, А₂, …, А_n. Числа l₁, l₂, ... , l_n называ.тся коэффициентами разложения вектора В по системе А₁, А₂, …, А_n.

5. Евклидовы пространства. Свойства длины вектора. Неравенство Коши-Буняковского.

6. Ортогональность векторов. Ортогональные системы векторов. Независимость попарно ортогональных векторов. Ортогональная проекция вектора на подпространство.

7. Ортонормированная система векторов. Построение ортонормированного базиса ортогонализацией произвольного базиса. Ортогональные матрицы.

8. Понятие матрицы. Виды матриц. Операции над матрицами. Свойства операций над матрицами. Транспонирование матриц. Приведение матриц к ступенчатому виду элементарными преобразованиями.

9. Определители квадратных матриц. Миноры и алгебраические дополнения. Свойства определителей. Определитель транспонированной матрицы. Определитель произведения матриц.

10. Обратная матрица. Алгоритм отыскания обратной матрицы. Построение обратной матрицы элементарными преобразованиями.

11. Ранг матрицы. Ранг ступенчатой матрицы. Неизменность ранга при элементарных преобразованиях. Теорема о ранге матрицы. Критерий линейной независимости системы строк (столбцов). Ранг произведения матриц.

12. Понятие системы линейных уравнений. Общая теория решения системы уравнений. Теорема Кронекера-Капелли о совместности системы линейных уравнений.

13. Методы решения системы уравнений: метод обратной матриц, формулы Крамера, метод Гаусса. Векторная запись системы уравнений.

14. Системы однородных линейных уравнений. Решение системы однородных уравнений. Фундаментальная система решений. Собственные значения и собственные векторы.

15. Базисные (главные) и свободные неизвестные. Геометрическая интерпретация систем линейных уравнений в случае двух или трех неизвестных. Ненулевые решения однородной системы уравнений.

16. Определение и примеры линейных операторов. Матрица линейного оператора. Преобразование матрицы линейного оператора при замене базиса.

17. Собственные векторы и собственные значения линейного опера-тора. Приведение матрицы линейного оператора к диагональному виду.

18. Характеристический многочлен линейного оператора. О корнях характеристического многочлена линейного оператора. Свойства собственных векторов с одинаковыми и различными собственными значениями.

19. Линейный функционал. Формула линейного функционала.

20. Матрица билинейной формы. Матрица симметричной билинейной формы. Преобразование матрицы билинейной формы при замене базиса.

21. Определение квадратичной формы. Преобразование квадратичных форм. Квадратичные формы канонического вида. Единственность симметричной билинейной формы, порождающей квадратичную форму.

22. Критерий Сильвестра положительной определенности квадратичной формы. Закон инерции для квадратичных форм. Билинейные формы.

23. Сопряженность операторов в евклидовом пространстве. Матрицы сопряженных операторов. Собственные векторы и собственные значения самосопряженных операторов. Ортонормированный базис из собственных векторов самосопряженного оператора. Приведение квадратичной формы к каноническому виду.

24. Преобразование координат точки при замене системы координат. Линейные отображения. Линейные операторы, связанные с линейными отображениями. Геометрические свойства линейных отображений. Аффинные и изометрические отображения.

25. Прямоугольная система координат на плоскости. Расстояние между точками. Деление отрезка в данном отношении.

26. Общее уравнение прямой на плоскости. Различные способы задания прямой на плоскости.

27. Параметрическое и каноническое уравнения прямой.

28. Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых.

29. Расстояние от точки до прямой. Преобразование координат точки при замене системы координат.

30. Векторное уравнение плоскости. Общее уравнение плоскости. Нормальное уравнение плоскости. Частные случаи расположения плоско-стей. Различные способы задания плоскости.

31. Угол между плоскостями. Условие параллельности и перпендикулярности плоскостей.

32. Уравнение прямой в пространстве. Различные способы задания прямой в пространстве. Угол между плоскостям. Взаимное расположение прямых и плоскостей.