1 курс / Теория вероятностей / Ответы на экзамен
.docx|
1.Основные понятия ТВ Опыт- испытание Событие-результат испытания Достоверное событие-событие, которое обязательно произойдет при испытании. Невозможное событие- событие, которое заведомо не произойдет при испытании. Случайное событие- событие, которое в результате эксперимента может либо произойти, либо не произойти Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании. Два события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании. Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью. Каждое равновозможное событие, которое может произойти в данном опыте называется элементарным исходом. Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта. Вероятность события А равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
2.Понятие частоты Относительной частотой события А, называется отношение числа испытаний, в котором появилось событие А, к общему числу произведенных испытаний.
где mA - число экспериментов, в которых появилось событие А; n - общее число экспериментов.
|
3. Понятие вероятности события.
Вероятность
Р(А) события А равна
отношению числа благоприятствующих
исходов к общему числу возможных
исходов. С в о й с т в о 1. Вероятность достоверного события равна единице. Р (A) = m / n = n / n = 1. С в о й с т в о 2. Вероятность невозможного события равна нулю. Р (А) = m / n = 0 / n = 0. С в о й с т в о 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. 0 < Р (А) < 1 Геометрическое определение вероятности. Пусть в некоторую область случайным образом бросается точка T, причем все точки области W равноправны в отношении попадания точки T. Тогда за вероятность попадания точки T в область A принимается отношение
где S(A) и S(W) — геометрические меры (длина, площадь, объем и т.д.) областей A и W соответственно.
|
4. Действия над событиями
1. Сумма
(объединение) событий (рис. 4.2)
представляет собой сложное событие,
состоящее в появлении хотя бы одного
из событий А и В. Объединение событий
обозначается как
2. Произведением
(пересечением) событий А и В называется
их совместное появление (рис. 4.3).
Обозначается произведение событий
как 3. Достоверным событием называется событие, которое обязательно происходит в результате данного испытания (рис. 4.4). Оно обозначается обычно как Е.
4. Невозможное
событие – событие, которое не может
произойти в результате данного
испытания. Принятое обозначение –
5.
Несовместными называются события,
которые в результате данного испытания
не могут произойти вместе (рис. 4.5).
Примеры несовместных событий: попадание
и промах при выстреле, выпадение двух
и трех очков при бросании игральной
кости. Рис. 4.5 наглядно показывает, что
для несовместных событий
6. Противоположным
к А событием называется событие,
состоящее в непоявлении события А
(рис. 4.6). Обозначается противоположное
событие символом
|
5. Элементы комбинаторики Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.
Перестановкой из n элементов (например чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
|
|
6. Правило суммы. Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект B - может быть n способами, то выбрать либо A , либо B можно m+n способами. Правило произведения. Если некоторый объект A может быть выбран из совокупности объектов n способами и после каждого такого выбора другой объект B может быть выбран n способами, то пара объектов (A,B) в указанном порядке может быть выбрана m*n способами.
7.Cумма событий Суммой событий А и В называется событие А+В состоящее в наступлении хотя бы одного из них. Теорема: Вероятность суммы несовместных событий А и В равны сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В)
8. Независимые и зависимые события Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А зависит от того, произошло событие В или нет. Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.
9. Теорема умножения вероятностей для зависимых и независимых событий "Теорема умножения для независимых событий" имеет вид P(AB)=P(A)*P(B), т.е. вероятность появления двух независимых событий равна произведению вероятностей этих событий. "Теорема
умножения для независимых событий"
имеет вид P(AB)=P(A)*
10. Теория сложения вер-ей для совместн.событий Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
11. Произведение двух и более событий Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.
|
12. Формула полной вер-ти и ф.Байеса
Пусть
Пусть
событие
13. Повторные независ. испытания- многократные испытания, в которых вероятность появления события А в каждом испытании не изменяется в зависимости от исходов других испытаний Под
схемой Бернулли понимают конечную
серию
|
14. Локальная теорема Лапласа.
Локальная
теорема Муавра-Лапласа. Если
вероятность появления события А в
каждом из n
15. Интегральная теорема Муавра-Лапласа. Пусть
вероятность появления события А в
каждом из n (n→∞)независимых
испытаний равна одной и той же
постоянной р (0<р<1),
то вероятность
|
16. Теорема Пуассона
При большом числе испытаний постоянной малой вероятности наступления события А в каждом испытании р 0 и при выполнении условия 0,1 ≤np≤10, вероятность того что в n независимых испытаниях событие А наступит ровно m раз, определяется в соответствии с теоремой Пуассона:
n- число испытаний Бернулли m- число испытаний, в котором наступило событие А
17. Наивероятнейшее число наступления события.
Наивероятнейшее
число
18. Вероятность появления А в n независимых испытаниях хотя бы один раз.
Вероятность появления хотя бы одного из 2 совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления Р(А+В)=Р(А)+Р(В)-Р(АВ)
19. Случайные величины. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. |
|
20. Закон распределения дискретной случайной величины Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Например, денежный выигрыш в какой-нибудь лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством) Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д. Закон распределения дискретной случайной величины представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σpi = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (xi; pi)Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x: F(X) = P(ξ < X). Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного..Закон распределения вероятностей дискретной случайной величины.
21.Математическое ожидание дискретной случайной величины. Свойства Числа, которые описывают случайную величину суммарно, называют числовыми характеристиками случайной величины. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
Замечание. Вышеприведенная формула справедлива для дискретной случайной величины, число возможных значений которой конечно. Если же случайная величина имеет счетное число возможных значений, то для нахождения математического ожидания используют формулу:
причем это математическое ожидание существует при выполнении соответствующего условия сходимости числового ряда в правой части равенства. Вероятностный смысл математического ожидания: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величин Свойства математического ожидания
|
22. Дисперсия дискретной случайной величины, ее свойства.
Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания D(X) = M(X – M(X))^2. Для вычисления удобнее пользоваться формулой: D(X) = M(X^2) – (M(X))^2.
Свойства: 1. Дисперсия постоянной величины равна 0: D( C ) = 0, 2. Постоянный множитель можно выносить за знак диперсии, возводя его в квадрат: D (CX) = C^2 D(X), 3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин: D (X+Y+Z) = D(X) + D(Y) + D (Z) 4. Дисперсия суммы постоянной величины и случайной – равна дисперсии случайной величины D(C+X) = D(X).
23. Биномиальное распределение. Дискретная случайная величина X имеет биноминальное распределение, если ее закон распределения описывается формулой Бернулли:
где
p – параметр распределения Распределение зависит от двух параметров п и р. На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из п испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в п опытах, имеет биноминальное распределение. Числовые характеристики: М [Х] = n, D[X]= npq. Название объясняется тем, что правую часть равенства можно рассматривать как общий член разложения Бинома Ньютона:
24. Геометрическое распределение. Дискретная случайная величина X имеет геометрическое распределение, если вероятности ее возможных значений 0,1,….,k,.. определяются так:
где
p – параметр распределения,
На практике геометрическое распределение появляется при следующих условиях. Пусть производится некоторый опыт, в котором некоторое событие появляется с вероятностью p. Опыты производятся последовательно, до наступления события. Случайная величина X, равная числу неудачных опытов, имеет геометрическое распределение.
Числовые характеристики геометрического распределения:
|
25.Равномерное распределение непрерывнои величины. Показательное распределение. Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение. Плотность вероятности равномерного распределения имеет вид:
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью
Итак,
26. Распределение Пуассона.
Одно из важнейших распределений вероятностей случайных величин, принимающих целочисленные значения. Подчинённая П. р. случайная величина Х принимает лишь неотрицательные значения, причём Х = kc вероятностью
|
|
27. Непрерывные случайные величины. Функция распределения. Интегральный закон распределения.
Закон распределения непрерывной случайной величины нельзя задать также, как для дискретной. Он неприменим в силу того, что нельзя перечислить все бесконечное несчетное множество значений, а вероятности каждого отдельно взятого значения непрерывной случайной величины равны нулю. Для описания закона распределения непрерывной случайной величины Х предлагается другой подход: рассматривать не вероятности событий Х=х для разных х, а вероятности события Х<х. При этом вероятность P(X<x) зависит от текущей переменной, т. е. является некоторой функцией от х. Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х:
Функцию F(x) называют интегральной функцией распределения или интегральным законом распределения. Способ задания непрерывной случайной величины с помощью функции распределения не является единственным. Необходимо определить некоторую функцию, отражающую вероятности попадания случайной точки в различные участки области возможных значений непрерывной случайной величины. Т. е. представить некоторую замену вероятностям pi для дискретной случайной величины в непрерывном случае. Такой функцией является плотность распределения вероятностей. Плотностью вероятности (плотностью распределения, дифференциальной функцией) случайной величины Х называется функция f(x), являющаяся первой производной интегральной функции распределения:
Про
случайную величину Х говорят, что она
имеет распределение (распределена) с
плотностью f(x) на определенном участке
оси абсцисс. Равномерный закон
распределения. Непрерывная случайная
величину Х имеет равномерный закон
распределения (закон постоянной
плотности) на отрезке [a; b], если на этом
отрезке функция плотности вероятности
случайной величины постоянна, т.е.
f(x) имеет вид:
34.Интегральная и дифференциальная ф-ии нормального распределения.Кривая Гаусса. Интегральной функцией распределения непрерывной случайной величины X называется ф-ия F(x),равная вероятности того,что X приняла значение,меньше x:F(x)=P(X<x) F(x)-геометрический смысл этого равенства,это вер-ть того,что случ.величина X примет значение,которое изображается на числовой оси точкой,лежащей левее точки x.Функция распределения совершенно так же определяется для дискретных случайных величин. Плотностью распределения вероятностей непрерывной случ.величины(дифференц.ф-ей распр-я)называют первую производную от ф-ии распределения: F’(x)=f(x) Ф-ия
F(x)
общего нормального распределения
F(x)= Нормальной кривой Гаусса назыв. график плотности нормального распределения.
35. Понятие и примеры системы случаиных величин. Случайной величиной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Более строгое определение случайной величины можно дать следующим образом: Случайной величиной называется функция X(ω), определенная на некотором множестве элементарных событий Ω. Случайные величины обычно обозначают большими буквами X, Y, Z , а их возможные значения – соответствующими строчными буквами x, y, z. Пример 1 Число родившихся мальчиков (или девочек) среди ста новорожденных. Пример2 Число появлений герба при четырех бросаниях монеты. Пример3 Время безотказной работы некоторого прибора.
|
28. Непрерывные случайные величины. Плотность распределения вероятностей непрерывной случайной величины. Дифференциальная функция распределения. Функцией распределения вероятностей называют функцию , определяющую вероятность того, что случайная величина в результате испытания примет значение, меньшее , то есть: . Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Свойства функции распределения вероятностей случайной величины
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале , равна приращению функции распределения вероятностей на этом интервале:
Следствие
2. Вероятность того, что непрерывная
случайная величина примет одно
определенное значение, равна нулю. Используя последнее следствие, легко убедиться в справедливости следующих равенств:
Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения: ; Плотностью распределения вероятностей непрерывной случайной величины называют функцию – первую производную от функции распределения вероятностей : . Таким образом, функция распределения вероятностей является первообразной для плотности распределения вероятностей. Теорема. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения, взятому в соответствующих пределах: . Следовательно, зная плотность распределения вероятности , можно найти функцию распределения по формуле
36. Характеристика закона больших чисел. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли. Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшим. Приведем данные теоремы и неравенство Чебышева без доказательств. Неравенство
Чебышева (оценка снизу):
Вероятность того, что отклонение
случайной величины X
от ее математического ожидания по
абсолютной величине меньше положительного
числа ε , не меньше, чем
|
29.Нахождение интегральной функции распределения через дифференциальную ф-ию.Вероятность попадания непрерывной случ.величины в заданный интервал. Теорема.В-ть
попадания непрерывной случ.величины
X
в интервале(a,b)
равна определенному интегралу от ее
плотности вер-ти,взятому в пределах
от a
до b
P(-a<X<b)= F(x)=
30. Математическое ожидание непрерывнои случаинои величины. Математическим
ожиданием непрерывной случайной
величины
X,
возможные
значения которой принадлежат отрезку
[a,b],
называют определенный интеграл
Если
возможные значения принадлежат всей
оси Ox
, то
31. Дисперсия непрерывнои случ.величины. Стандартное отклонение. Дисперсиеи
непрерывнои случ.величины наз-ют
мат.ожидание квадрата ее отклонения.Если
возможные значения Х принадлежат
отрезку [а,в], то: M(x)=
|
32 Нормальное распределение непрерывнои случаинои величины и его параметры. Плотность вероятности нормированного нормального распределения таблица значении этои функции. Нормальным
называют распределение вероятностей
непрерывной случайной величины,
которое описывается следующей
плотностью вероятностей:
33. Вероятность попадания нормального распределения случ.величины в заданный интервал.Вер-ть заданного отклонения.Правило трех сигм. В-ть
попадания нормально распределенной
случайной величины X
в интервале(α,β) определяется по
формуле:P(α<X<β)=ϕ( Вероятность
отклонения нормально распределенной
случ.величины от матем.ожидания по
абсолютной величине меньше,чем на
δ(δ>0),определяется по формуле:P(│x-a│<σ)=2ϕ( Правило трех сигм. Полагая в выражении (3)σ=3σ,получим P(│x-a│<3σ)=2ϕ(3)
39. Математическое ожидание и дисперсия функции одного случ.аргумента для двух случаев: аргумент – непрерывная случ.величина. Мат.ожиданием
непрерывнои случ.величины Х, возможные
значения которои принадлежат отрезку
[а,в], наз-ют определенныи интеграл.M(x)=
40. Задачи мат.статистики. Генеральная и выборочная совокупности. Повторная и бесповторная выборки. Репрезентативная выборка. Мат.статистика занимается обработкои результатов случ.эксперимента. ее задачи: 1)Разработка методологии сбора и группировки статистического материала, полученного в результате наблюдении за случ.процессами.2)разработка методов анализа получаемых статистических данных. Этот анализ включает оценку вероятностеи события, функции плотности вероятности, оценку параметров известного распредделения. Генеральнои совокупностью наз-ся множество объектов произвольнои природы, обладающих признаками, доступными для наблюдения и количественного изменения. Распределение Х часто наз-ют распределением генеральнои совокупности. Выборочная совокупность — множество случаев с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании. Если выборки делают по одному объекту, которыи обследуют и снова возвращают в генеральную совокупность, то выборка наз-ся повторнои.Если объекты выборки уже не возвращают, то безповторнои. Репрезентативная выборка - это выборка из генеральной совокупности с распределением F(x), представляющая основные особенности генеральной совокупности.
|
|
37. Понятие функции одного случайного аргумента. Нахождение распределения функции по известному распределению дискретного и непрерывного аргумента. Если
каждому возможному значению случайной
величины Х
соответствует одно возможное значение
случайной величины Y,
то
Y
называют
функцией
случайного аргу-мента Х:
Y
= φ(X).
Пусть задана функция Y
= А)
Если различным возможным значениям
аргумента X
соответствуют различные возможные
значения функции Y,
то вероятности соответствующих
значений X
и Y
между собой равны, так как событие
“величина X
приняла значение xi”
влечет за собой событие “величина Y
приняла значение
38. Математическое ожидание и дисперсия функции одного случ.аргумента для двух случаев: аргумент – дискретная случ величина. Пусть
некоторая дискретная случ величина
Х с конечным числом своих значении
задана законом распределения.
Мат.ожиданием М(Х) дискретнои
случ.величины Х наз-ся сумма произведении
всех возможных значении величины Х
на соответствующие вероятности.
М(Х)=х1р1 + х2р2+… D(X)=M(
|

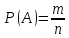
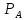 (B)
(B)
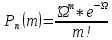 ;
ƛ=np
;
ƛ=np
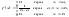 Функция
распределения вероятностей равномерной
случайной величины имеет вид:
Функция
распределения вероятностей равномерной
случайной величины имеет вид:
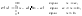
 где
где
 - постоянная положительная величина.
функцию
распределения показательного закона
:
- постоянная положительная величина.
функцию
распределения показательного закона
: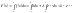 .
.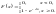
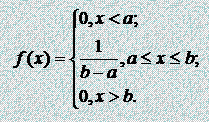
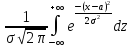 ,а
ф-ия нормированного распределения
,а
ф-ия нормированного распределения
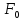 (x)=
(x)=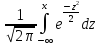 .Ф-ия
.Ф-ия
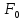 (x)
табулирована.Легко проверить,что
F(x)=F((x-a)/σ)
(x)
табулирована.Легко проверить,что
F(x)=F((x-a)/σ) :
:
 .
Неравенство
Чебышева
(оценка
сверху):
Вероятность
того, что отклонение случайной величины
X
от ее математического ожидания по
абсолютной величине не меньше
положительного числа ε , меньше или
равна
.
Неравенство
Чебышева
(оценка
сверху):
Вероятность
того, что отклонение случайной величины
X
от ее математического ожидания по
абсолютной величине не меньше
положительного числа ε , меньше или
равна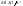 :
: .
Теорема Чебышева: Если
X1,
X2…..Xn,…-
попарно независимые случайные величины,
причем дисперсии их равномерно
ограничены (не превышают постоянного
числа C)
,то, как бы мало ни было положительное
число ε, вероятность неравенства
.
Теорема Чебышева: Если
X1,
X2…..Xn,…-
попарно независимые случайные величины,
причем дисперсии их равномерно
ограничены (не превышают постоянного
числа C)
,то, как бы мало ни было положительное
число ε, вероятность неравенства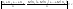 будет
как угодно близка к единице, если число
случайных величин достаточно велико.
Другими
словами, в условиях теорем
будет
как угодно близка к единице, если число
случайных величин достаточно велико.
Другими
словами, в условиях теорем .
Теорема
Бернулли: Если
в каждом из n
независимых испытаний вероятность p
появления события A
постоянна, то как угодно близка к
единице вероятность того, что отклонение
относительной частоты от вероятности
p
по абсолютной величине будет сколь
угодно малым, если число испытаний
достаточно велико.
.
Теорема
Бернулли: Если
в каждом из n
независимых испытаний вероятность p
появления события A
постоянна, то как угодно близка к
единице вероятность того, что отклонение
относительной частоты от вероятности
p
по абсолютной величине будет сколь
угодно малым, если число испытаний
достаточно велико.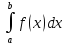 . В частности,если f(x)-четная
ф-ия и концы интервала симметричны
относительно начала координат,то
P(-a<X<a)=P(│X│<a)=2
. В частности,если f(x)-четная
ф-ия и концы интервала симметричны
относительно начала координат,то
P(-a<X<a)=P(│X│<a)=2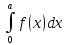
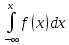 позволяет найти интегральную ф-ию
распределения F(x)
по ее плотности вероятности.
позволяет найти интегральную ф-ию
распределения F(x)
по ее плотности вероятности.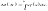
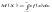 Замечание:
Предполагается, что несобственный
интеграл сходится абсолютно, то есть
существует интеграл
Замечание:
Предполагается, что несобственный
интеграл сходится абсолютно, то есть
существует интеграл
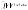
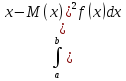 .
Если возможные значения принадлежат
всеи оси, то: M(x)=
.
Если возможные значения принадлежат
всеи оси, то: M(x)=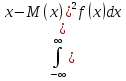 .
Так как D(X)
= M(X2)
– [M(X)]2,
то можно использовать следующие
формулы для вычисления дисперсии:
.
Так как D(X)
= M(X2)
– [M(X)]2,
то можно использовать следующие
формулы для вычисления дисперсии: или
или
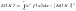 .Замечание:
Свойства математического ожидания и
дисперсии дискретных случайных величин
сохраняются и для непрерывных величин.
Среднее
квадратическое отклонение непрерывной
случайной величины
определяется аналогично дискретному
случаю:
.Замечание:
Свойства математического ожидания и
дисперсии дискретных случайных величин
сохраняются и для непрерывных величин.
Среднее
квадратическое отклонение непрерывной
случайной величины
определяется аналогично дискретному
случаю:
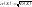 .
.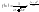 ,
где
,
где
 .
Стандартным
нормальным
или нормированным
называют нормальное распределение
с параметрами
.
Стандартным
нормальным
или нормированным
называют нормальное распределение
с параметрами
 и
и
 .
Например, если X
– нормальная величина с параметрами
.
Например, если X
– нормальная величина с параметрами
 и
и
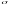 ,
то
,
то
 -
стандартная нормальная величина,
причем
-
стандартная нормальная величина,
причем
 и
и
 .
Плотность стандартного нормального
распределения имеет вид
.
Плотность стандартного нормального
распределения имеет вид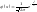 .Функция
распределения
.Функция
распределения
 нормального распределения имеет вид:
нормального распределения имеет вид:
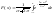 .
Функция распределения
.
Функция распределения
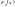 стандартного
нормального распределения имеет вид:
стандартного
нормального распределения имеет вид:
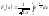 .
.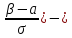 ϕ
ϕ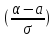
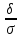 )
(3)
)
(3)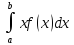 .
Если возможные значения принадлежат
всеи оси Ох, то: M(x)=
.
Если возможные значения принадлежат
всеи оси Ох, то: M(x)=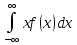 .
Дисперсиеи непрерывнои случ.величины
наз-ют мат.ожидание квадрата ее
отклонения.Если возможные значения
Х принадлежат отрезку [а,в], то:
M(x)=
.
Дисперсиеи непрерывнои случ.величины
наз-ют мат.ожидание квадрата ее
отклонения.Если возможные значения
Х принадлежат отрезку [а,в], то:
M(x)=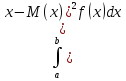 .
Если возможные значения принадлежат
всеи оси, то: M(x)=
.
Если возможные значения принадлежат
всеи оси, то: M(x)=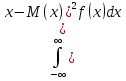 .
Среднее квадратическое отклонение
равно корню из дисперсии.
.
Среднее квадратическое отклонение
равно корню из дисперсии. (X)
случайного аргумента X,
где аргумент X
– дискретная случайная величина с
возможными значениями x1,
x2,…
xn
,вероятности
которых соответственно равны p1,
p2,…
pn.
Очевидно, Y
- также дискретная случайная величина
с возможными значениями
(X)
случайного аргумента X,
где аргумент X
– дискретная случайная величина с
возможными значениями x1,
x2,…
xn
,вероятности
которых соответственно равны p1,
p2,…
pn.
Очевидно, Y
- также дискретная случайная величина
с возможными значениями

 (xi)”,
то вероятности возможных значений Y
соответственно равны p1,
p2,…
pn.
b)
Если различным возможным значениям
X
соответствуют значения Y,
среди которых есть равные между собой,
то следует складывать вероятности
повторяющихся значений Y.
(xi)”,
то вероятности возможных значений Y
соответственно равны p1,
p2,…
pn.
b)
Если различным возможным значениям
X
соответствуют значения Y,
среди которых есть равные между собой,
то следует складывать вероятности
повторяющихся значений Y.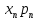 .
Теорема: Мат.ожидание дискр.случ.величины
Х приближенно равно среднему арифмет.всех
ее значении(при достаточно большом
числе испытании) Хср=М(Х). Матем.ожидание
случ.величины можно приближенно
считать ее средним значением, что и
делают на практике. Дисперсиеи D(X)
дискретнои случ.величины Х наз-ся
мат.ожидание квадрата отклонения
случ.величины от ее мат.ожидания.
D(x)=M[(X
– M(X)
.
Теорема: Мат.ожидание дискр.случ.величины
Х приближенно равно среднему арифмет.всех
ее значении(при достаточно большом
числе испытании) Хср=М(Х). Матем.ожидание
случ.величины можно приближенно
считать ее средним значением, что и
делают на практике. Дисперсиеи D(X)
дискретнои случ.величины Х наз-ся
мат.ожидание квадрата отклонения
случ.величины от ее мат.ожидания.
D(x)=M[(X
– M(X)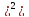 .
Из закона распределения величины [X
– M(X)
.
Из закона распределения величины [X
– M(X)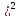 следует, что D(x)=M[(X1
– M(X)
следует, что D(x)=M[(X1
– M(X)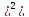 p1
+ M[(X2
– M(X)
p1
+ M[(X2
– M(X)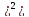 p2
+…. M[(Xn
– M(X)
p2
+…. M[(Xn
– M(X)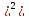 pn.
Теорема: Дисперсия равна разности
между мат.ожид. квадрата случ.величины
Х и квадратом ее мат.ожидания:
pn.
Теорема: Дисперсия равна разности
между мат.ожид. квадрата случ.величины
Х и квадратом ее мат.ожидания: