
1 семестр / Физика - 2 / лабораторные работы / lab76
.pdf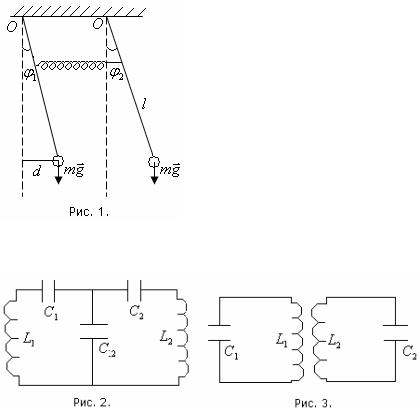
Лабораторная работа №76.
«ИЗУЧЕНИЕ СВЯЗАННЫХ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ».
Цель работы: изучение особенностей и основных характеристик систем с несколькими степенями свободы на примере двух связанных простых колебательных систем.
Приборы и принадлежности: установка из пары связанных пружинами маятников, секундомер, линейка, легкая металлическая рейка.
КРАТКАЯ ТЕОРИЯ.
До сих пор мы изучали колебательные системы, для определения состояния которых требовалось знать закон изменения только одной величины. Для математического или физического маятников это смещение x или угол отклонения ϕ . Для колебательного контура - заряд q и т. д. Это системы с
одной степенью свободы. Каждая из этих систем характеризуется одной собственной частотой колебаний.
Числом степеней свободы
называется число независимых величин, с помощью которых однозначно определяется состояние системы.
В природе существует множество колебательных систем, так или иначе связанных друг с другом. В механике, например, такую систему с двумя степенями
свободы |
образуют |
два |
математических |
|
маятника массой |
m и длиной l , связанные |
|||
невесомой |
пружиной |
с |
коэффициентом |
|
жесткости k (рис. 1.). |
|
|
||
В |
электродинамике |
аналогом двух |
||
связанных маятников является электрическая |
||||
цепь, состоящая из двух колебательных |
||||
контуров LC , связанных общей емкостью C12 |
(рис. 2) |
или связанные |
||
индуктивно (рис. 3). Колебательные системы, между которыми имеется связь,
посредствам которой они взаимодействуют друг с другом, называются связанными. Это системы с двумя степенями свободы. Для задания их состояния требуется две величины. В отличии от одиночного маятника, уединенного контура, эти системы имеют две собственные частоты.
Вобщем случае движение системы с двумя степенями свободы очень сложно, непохожее на простое гармоническое колебания. Однако можно показать, что при линейных уравнениях движения это сложное движение связанной системы с двумя степенями свободы может быть представлено как суперпозиция двух независимых простых гармонических колебаний, происходящих одновременно. Эти простые гармонические колебания, с помощью которых может быть представлено сложное движение связанной системы, называется нормальными или собственными колебаниями, или гармониками, или нормальными модами, или простыми модами. Частоты, соответствующие этим гармоникам или модам, называются нормальными частотами.
Задавая определенные начальные условия, можно в связанной системе возбудить колебания, соответствующие одной нормальной моде или гармонике.
Вслучае двух связанных маятников первая мода возникает, если в системе возбудить синфазные колебания, а другая – при возбуждении антифазных колебаний.
Найдем частоты этих мод или нормальные частоты.
Для возбуждения синфазных колебаний оба связанных маятника
отклоняют на одинаковый малый (5 −100 ) угол ϕ1 =ϕ2 в одну и ту же сторону от положения равновесия (рис. 1). Воспользуемся основным законом
вращательного движения вокруг неподвижной оси O : |
|||
JεG = ∑M внешн. |
или |
JεG = M тяж. + Мупр. (1) |
|
где МGтяж. |
-- момент силы тяжести; |
|
|
G |
|
|
|
Мупр. |
-- момент силы упругости; |
|
|
J-- момент инерции маятника относительно оси O ,
ε-- его угловое ускорение.
Так как пружина не деформирована, сила упругости, а следовательно, и M упр. = 0 . Тогда равенство (1) в скалярной форме переписывается в виде:
Jε = −M тяж. |
(2) |
Знак (−) означает, что момент силы тяжести стремится вернуть маятник в
положение равновесия. Так как ε = |
d 2ϕ |
, M тяж. = mgd , где m -- масса |
|
dt 2 |
|||
|
|
маятника; d -- плечо силы тяжести, то равенство (2) можно представить в виде:
J |
d 2ϕ |
= −mgd |
(3) |
||
dt |
2 |
||||
|
|
|
|||
или, если d = l sin ϕ , а т. к. угол ϕ мал, то sin ϕ ≈ϕ и d = lϕ , в виде:
Jd 2ϕ + mglϕ = 0 . dt 2
Разделив обе части этого равенства на J , получим дифференциальное уравнение гармонического колебания для величины ϕ :
|
|
|
d 2ϕ |
+ |
|
mgd |
|
ϕ = 0 , |
|
|
|
|
(4) |
|
|||
|
|
|
dt 2 |
|
|
J |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где, |
очевидно, |
mgd |
|
=ωc2 |
-- есть квадрат циклической частоты синфазных |
||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
J |
|
|
|
|
|
|
|
|
колебаний. |
Подставив значение J ≈ ml 2 , где |
l -- длина маятника, получим |
|||||||||||||||
ωc |
= |
g |
|
, следовательно, частота синфазных колебаний: |
|
||||||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
c |
= |
1 |
g . |
|
|
|
|
(5) |
|
|||||
|
|
|
|
|
2π |
l |
|
|
|
|
Рассмотрим |
антифазные |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
колебания маятников, для чего разведем |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
маятники |
в |
противоположные стороны |
|||
|
|
|
|
|
|
|
|
|
|
|
|
на один |
и |
тот же |
небольшой угол |
||
|
|
|
|
|
|
|
|
|
|
|
|
(5 −100 ) |
ϕ1 = −ϕ2 . При этом пружина |
||||
|
|
|
|
|
|
|
|
|
|
|
|
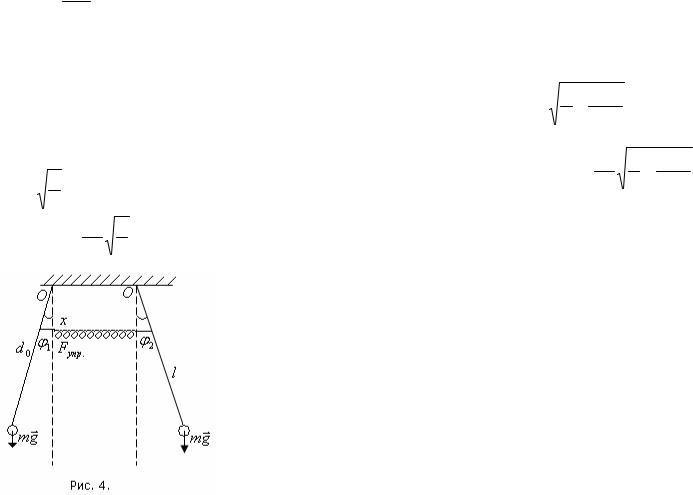
деформируется на величину 2x (рис. 4). |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Теперь кроме силы тяжести на маятник |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
будут |
действовать |
силы упругости: |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Fупр. |
= 2kx . |
|
||
Уравнение |
|
|
динамики |
вращательного движения |
запишется |
в виде: |
|||||
G |
G |
|
|
+ Мупр. |
|
|
|
|
|||
Jε = M тяж. |
|
|
|
|
|||||||
или в скалярной форме: |
|
Jε = M тяж. − Мупр. . |
(6) |
||||||||
|
Так как M упр. = Fупр. d0 = 2kxd0 , |
|
|
||||||||
где d0 |
-- расстояние от оси O до связи (пружины); |
k -- жесткость пружины, |
|||||||||
x = d0ϕ, то равенство (6) перепишется в виде: |
|
|
|||||||||
|
|
d |
2 |
ϕ |
|
|
|
2 |
|
|
|
|
|
|
mgd |
|
2kd0 |
|
|
|
|||
|
|
|
|
|
|
|
+ |
|
ϕ = 0 |
(7) |
|
|
|
dt |
2 |
J |
J |
||||||
|
|
|
|
|
|
|
|
||||
Получили дифференциальное уравнение антифазных колебаний.
|
|
ωa2 = |
mgd |
+ |
2kd 2 |
|
|
|
J ≈ ml 2 , |
|||||||
Здесь |
|
|
|
|
|
0 |
, |
или |
учитывается, |
что |
||||||
|
|
J |
|
J |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ωa = |
g |
+ |
2kd 2 |
-- циклическая частота антифазных колебаний, а частота |
||||||||||||
l |
|
|
ml |
0 |
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
антифазных колебаний: |
|
|
|
|
|
|
||||||||||
|
ν |
|
= |
1 |
|
|
g |
+ |
2kd 2 |
|
|
|
(8) |
|||
|
a |
2π |
|
l |
ml |
0 . |
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
Таким образом, в рассмотренной системе возникают две нормальные |
|||||||||||||||
моды с частотами νa |
и νa . |
|
|
|
|
|
|
|||||||||
Изменяя силу связи, т. е. k и d0 , можно получить очень близкие по
частоте две нормальные моды. Если систему привести в движение произвольным образом, возникает сложное движение, которое будет суперпозицией двух близких мод:
ϕ1 (t)= A1 cos(ωct +α1 )+ A2 cos(ωat +α2 ).

|
|
|
|
|
ϕ1 (t)= 2 Acos ∆ω t cos |
ωc +ωa t , |
(9) |
||
|
|
|
|
|
2 |
2 |
|
||
где |
|
2 Acos |
∆ω t |
|
-- амплитуда биения, ∆ω -- циклическая частота биений, |
||||
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
а |
2π |
=T |
-- период биения. |
|
|
||||
∆ω |
|
|
|||||||
|
б |
|
|
|
|
|
|||
Графически биение 1-го маятника изображены на рис. 5а.
Для возбуждения биения отклоним один маятник на 2 A , а второй будем удерживать в нулевой точке. Затем одновременно отпустим оба
маятника. Амплитуда колебаний (а, следовательно, и энергия E ) первого маятника уменьшается, а второго – возрастает (см. рис. 5б.). Через 12 Tб первый
маятник остановится, а второй будет иметь амплитуду ≈ 2A . При этом энергия колебаний переходит от одного маятника к другому полностью. Этот процесс будет периодически повторятся. Один полный оборот энергии от первого маятника ко второму и опять к первому и представляет одно биение (рис. 5в). Очевидно, что этот полный оборот энергии колебаний происходит за время,
равное периоду биения Tб . |
|
|
Если |
∆ω =ωa −ωc |
-- циклическая частота биения, то частота |
биения: |
|
|
νб |
=νа −νс . |
(10) |
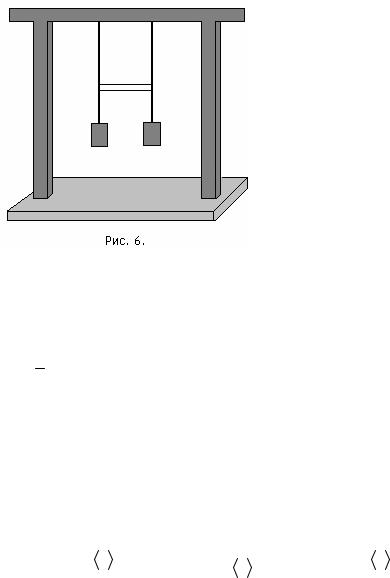
ОПИСАНИЕ УСТАНОВКИ Установка состоит из связанных пружинами маятников, укрепленных
на штативе (рис. 6). Для отклонения маятников на небольшую величину в ту или другую сторону от положения равновесия в установке предусмотрено отчетное устройство, содержащие металлическую линейку и одновременно фиксирующее колебания маятника строго вдоль этой линейки. Для удобства наблюдения синфазных колебаний связанных маятников в устройстве предусмотрена возможность соединения их металлической рейкой.
Положим для простаты α1 =α2 |
= 0 ; если ωa −ωc = ∆ω <<ωcp |
ωa +ωc , |
|
|
2 |
то возникают так называемые биения. Эффект биения будет наибольшим, если
A1 = A2 = A . Тогда уравнение биения примет вид:
СОДЕРЖАНИЕ КОНТРОЛЬНЫХ ВОПРОСОВ 1. Что собой представляет связанная система? Примеры.
2. Что называют числом степенной свободы?
3. Какие колебания называют нормальными или модами?
4. Какие колебания называют синфазными?
5. Выведите уравнения синфазных колебаний, частоты этих колебаний. 6. Какие колебания называются антифазными?
7. Выведите уравнение антифазных колебаний. Какова частота антифазных колебаний?
8. Дайте определение явлению биения.
9. Получите уравнение биений.
10. Дайте определение периода биений.
11. Какова схема установки? Каков порядок выполнения работы?
ВЫПОЛНЕНИЕ РАБОТЫ 1. Соединить маятники металлической рейкой, возбудить синфазные
колебания маятников, отклонить их на малый (5 −100 ) угол. Измерить время 8
– 10 полных колебаний и рассчитать частоту синфазных колебаний по формуле
νc = nt , где n -- число колебаний, t -- время. Измерение повторить 5 – 6 раз.
2.Провести аналогичные измерения для антифазных нормальных колебаний связанных маятников.
3.Придерживая перед пуском один и отклонив другой маятник, добиться возникновения биений колебаний связанных маятников. Определить частоту биений.
4.Измерив d и l , зная k и m , рассчитать частоты синфазных, антифазных колебаний и биений по формулам (4), (6), (8).
5.Данные занести в таблицу.
|
Синфазные |
|
Антифазные |
|
|
Биения |
|
|
|
||||
№ |
колебания |
|
колебания |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
п/п |
νопыт. |
ν |
νтеор. |
ν |
опыт. |
|
ν |
ν |
теор. |
νопыт. |
ν |
ν |
теор. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
