
1 семестр / Физика - 2 / лабораторные работы / lab74
.pdf
Лабораторная работа № 74.
ИЗУЧЕНИЕ МЕХАНИЧЕСКИХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ.
КРАТКАЯ ТЕОРИЯ.
Свободные колебания реальных механических систем всегда затухают. Затухание возникает в основном из-за трения, сопротивления окружающей среды
и возбуждения в ней упругих волн. |
|
|
|
|||||||||||||
|
|
Рассмотрим |
|
систему, |
|
|
|
|||||||||
совершающую |
|
|
|
|
крутильные |
|
|
|
||||||||
затухающие |
|
колебания. |
Она |
|
|
|
||||||||||
представляет из себя брусок, |
|
|
|
|||||||||||||
подвешенный на струне, концы |
|
|
|
|||||||||||||
которой закреплены. На брусок |
|
|
|
|||||||||||||
для увеличения момента инерции |
|
|
|
|||||||||||||
может быть положен брусок. |
|
|
|
|||||||||||||
После |
отклонения |
бруска |
на |
|
|
|
||||||||||
небольшой угол ϕ |
|
от |
|
|
|
|
|
|||||||||
положения |
равновесия система |
|
|
|
||||||||||||
будет |
|
совершать |
|
свободные |
|
|
|
|||||||||
крутильные колебания. |
|
|
|
|
|
|
||||||||||
Получим |
|
дифференциальное |
|
|
|
|||||||||||
уравнение |
|
|
|
|
затухающих |
|
|
|
||||||||
крутильных |
колебаний. |
Чтобы выяснить, |
как изменяется |
со временем |
||||||||||||
ϕ(t)используем основной закон динамики вращательного движения: |
||||||||||||||||
|
|
|
G |
|
G |
+ M сопр |
|
|
|
|
|
|||||
|
|
Jε = M упр |
|
|
|
|
(1) |
|||||||||
Где J - |
момент инерции бруска, ε = |
d 2ϕ |
- угловое ускорение, |
M упр - момент |
||||||||||||
dt 2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сил упругости, M сопр - момент сил сопротивления. |
|
|||||||||||||||
M упр = −kϕ , |
|
k - коэффициент упругости. Для малых углов отклонения (малых |
||||||||||||||
скоростей |
вращения) |
M сопр = −rω, |
r - |
коэффициент |
сопротивления, |
|||||||||||
ω = |
dϕ |
- угловая скорость. Уравнение (1) в скалярной форме примет вид: |
||||||||||||||
|
||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
d 2ϕ |
+ r |
dϕ |
+ kϕ = 0 |
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
dt 2 |
|
|
|
dt |
|
|
|
|
|
|
|
|
d |
2ϕ |
|
+ |
|
r dϕ |
+ |
|
k |
|
ϕ = 0 |
|
|
|
|
|
|
|
|||||||||||
|
dt 2 |
|
|
J |
|
|
dt |
|
|
J |
|
|
|
|
|
|
|
|
|||||||||||
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
||||||||||||
Обозначив |
|
|
= 2β |
|
( β |
|
- коэффициент затухания) |
и |
=ω02 ( ω0 - |
||||||||||||||||||||
|
|
J |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
||||
циклическая частота свободных незатухающих колебаний), получим |
|
||||||||||||||||||||||||||||
|
d |
2ϕ |
|
|
|
|
|
|
|
|
dϕ |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
+ |
2β |
|
|
|
|
+ω0 ϕ = 0 . |
|
|
|
|
|
|
(2) |
|||||||||||
|
dt 2 |
|
|
dt |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решением этого уравнения при малом затухании является функции: |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ϕ(t ) =ϕ0 exp(−β t) cos (ω t +α) |
|
|
|
|
(3) |
||||||||||||||||
Получена зависимость угла поворота от времени, |
здесь ϕ0 |
- амплитуда |
|||||||||||||||||||||||||||
в начальный момент |
|
|
времени, ϕ0 exp(−β t) - амплитуда |
затухающих |
|||||||||||||||||||||||||
колебаний. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Частота затухающих колебаний: ω = |
|
ω02 − β2 |
|
|
|
|
(4) |
||||||||||||||||||||||
Быстроту затухания колебаний принято характеризировать |
|||||||||||||||||||||||||||||
логарифмическим декрементом затухания: |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(t) |
|
ϕ0 exp(− β t) |
|
= βT |
|
||||
|
|
|
|
|
|
|
|
|
|
|
δ = ln |
|
|
|
= ln |
ϕ0 exp(− β (t +T )) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A(t +T ) |
|
||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
A(t) |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
ln |
|
= NβT |
= Nδ |
|
|
|
|
(5) |
|||||||||||||
|
|
|
|
|
|
|
|
A(t + NT ) |
|
|
|
|
|||||||||||||||||
Выясним физический смысл коэффициента затухания. Обозначим через τ время, в течении которого амплитуда колебаний уменьшается в e раз.
Тогда |
ϕ0 exp (−β(t +τ)) |
= exp (−βτ) = |
1 |
, |
|||
ϕ0 exp (−β t) |
e |
||||||
|
|
|
|||||
а следовательно, βτ =1 и |
|
|
|
||||
|
β = |
1 |
|
|
|
(6) |
|
|
|
|
|
||||
|
τ |
|
|
|
|||
Отсюда ясен физический смысл коэффициента затухания: коэффициент затухания есть величина, обратная времени, за которое амплитуда колебаний уменьшается в e раз.
Выясним физический смысл логарифмического декремента затухания:
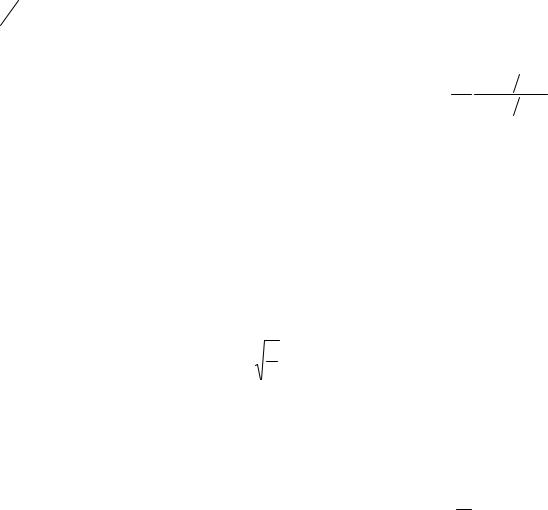
δ = βT = |
1 |
T = |
|
1 |
= |
1 |
, где |
|
τ |
|
Ne |
||||
|
τ |
T |
|
|
|||
|
|
|
|
|
|
|
|
Ne - число колебаний, происходящих за время τ .
Таким образом, логарифмический декремент есть величина, обратная числу колебаний, по завершению которых амплитуда уменьшается в e раз
(e = 2,72...).
|
|
|
Определим период затухающих колебаний. Выразим циклическую |
|||||||||||||||||||||||||
частоту |
|
затухающих колебаний |
ω |
и циклическую |
частоту |
собственных |
||||||||||||||||||||||
колебаний ω |
0 |
через соответствующие периоды T и T : |
ω = |
2π |
, |
ω |
0 |
= |
2π |
. |
||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
T |
|
|
|
T0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|||||
Учитывая, |
что |
коэффициент |
затухания |
связан |
с |
логарифмическим |
||||||||||||||||||||||
декрементом |
|
затухания отношением: |
|
β = |
δ |
из формулы (4) следует: |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T02 |
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
4π 2 |
= |
|
4π 2 |
− |
δ 2 , отсюда T 2 |
= |
|
|
(4π 2 +δ 2 ). |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
T 2 |
|
4π 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
T 2 |
|
|
|
T 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
||
Из выражения для собственной частоты крутильных колебаний ω02 |
= |
можно |
||||||||||||||||||||||||||
J |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
выразить |
период собственных |
крутильных |
колебаний: |
T |
= 2π |
J , тогда |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
k |
|
|
|
|||
период затухающих колебаний бруска: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
T1 = |
J |
(4π 2 +δ 2 ) |
|
|
|
|
|
|
|
|
|
|
|
(6) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если на брусок положить кольцо, момент инерции, а следовательно период колебаний увеличиться. Добавочный момент инерции,
создаваемый кольцом Jк = mr 2 , где m - масса кольца, r - его радиус. Для периода крутильных колебаний системы с кольцом:
T22 = |
J + Jк |
(4π 2 +δ22 ) |
(7) |
||||
k |
|||||||
|
T12 |
|
J (4π 2 +δ 2 ) |
|
|||
Возьмем отношение |
= |
и получим из нее расчетную |
|||||
T22 |
(J + Jк )(4π 2 +δ22 ) |
|
|||||
J = |
|
|
|
|
J кT12 (4π +δ22 ) |
|
J к |
|
|
||||
|
|
|
|
= |
|
|
|
|
|
|
|||
T22 (4π 2 +δ 2 )−T12 |
(4π 2 +δ22 ) |
|
T22 |
|
4π 2 +δ 2 |
−1 |
|||||||
|
T 2 |
4π 2 +δ 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
2 |
|
|
||||
J = |
|
|
|
|
Jк |
|
|
|
|
|
|
(8) |
|
|
T 2 |
1 +δ 2 4π 2 |
|
|
|
|
|
|
|||||
|
|
T |
2 |
1 +δ 2 4π 2 −1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
1 |
2 |
|
|
|
|
|
|
|
|
|||
Если δ 2π и |
|
δ2 2π то можно записать приближенную формулу: |
|||||||||||
J = |
|
|
J к |
|
|
|
|
|
|
|
(9) |
||
|
T |
2 |
−1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
T |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
Определив периоды колебаний T1 и T2 , момент инерции кольца Jк , можно определить момент инерции бруска J .
ВЫПОЛНЕНИЕ РАБОТЫ И ОБРАБОТКА РЕЗУЛЬТАТОВ.
1.Отводят брусок на угол ϕ0 ≈100 −150
время t , в течении которого брусок сделает N колебаний и измеряют ϕN - угол
отклонения бруска при последнем колебании. Чем больше число N , тем точнее измерения. Поэтому следует наблюдать возможно большее число колебаний
(N ≈ 20 −30). Каждое измерение повторяют 3 – 5 раз.
2.Проделывают то же самое с кольцом. При наложении кольца нужно возможно точнее обеспечить совпадение его центра с осью вращения системы. Для этого разрез и точка, отмеченная на кольце, должны отстоять на равных расстояниях от струны и располагаться на средней линии бруска. Точность установки проверяют, подставив линейку к кольцу и поворачивая брусок.
3.Рассчитывают периоды затухающих колебаний бруска и бруска с кольцом по
формуле T = Nt , логарифмические декременты затухания δ и δ2 , используя формулу (5) .
формулу для момента инерции бруска:

После вычисления логарифмических декрементов затухания решают, нужно ли
δ 2
учитывать в формулах (8) и (9) слагаемые вида 4π 2 .
4.Вычисляют среднее значение момента инерции бруска по формуле (8) или (9).
5.Сравнивают измеренное значение момента инерции бруска с теоретическим,
которое для однородного прямоугольного бруска находят по формуле:
JT |
= |
M |
(a2 |
|
+b2 ), где |
M - |
|
масса бруска, |
a - его |
длина, b |
|
- ширина. |
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
12 |
|
|
|
|
|
|
JT − J |
|
≤ J . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Проверяют соотношение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
6. |
Обрабатывают результаты прямых и косвенных измерений по методу |
||||||||||||||||||||||||||||||||
Стьюдента. Результаты измерений и вычислений заносят в таблицы 1, 2. |
|||||||||||||||||||||||||||||||||
|
|
|
|
Для бруска |
|
|
|
|
|
|
|
|
|
|
|
|
Для бруска с грузом |
||||||||||||||||
N |
|
ϕ0 |
N 1 |
ϕN |
t 1 |
T 1 |
δ |
|
∆δ |
|
ϕ0 |
|
N2 |
|
ϕN 2 |
|
t 2 |
|
T 2 |
δ 2 |
∆δ 2 |
||||||||||||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
m |
r |
Jк |
|
T1 |
T2 |
J |
|
εJ |
∆J |
|
J = J ± ∆J |
JT |
|
J N − J |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1.Сформулируйте основной закон динамики вращательного движения.
2.Выведите дифференциальное уравнение затухающих крутильных колебаний.
3.Запишите и проанализируйте формулу амплитуды затухающих колебаний.
4.Запишите и проанализируйте формулу циклической частоты затухающих колебаний.
5.Каков физический смысл коэффициента затухания?
6.Какая величина называется логарифмическим декрементом затухания? Каков его физический смысл?
7.Выведите формулу периода затухающих колебаний.
8.Выведите расчетную формулу для определения момента инерции бруска.
