Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Поволжский государственный университет телекоммуникаций и информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

lab20

.pdf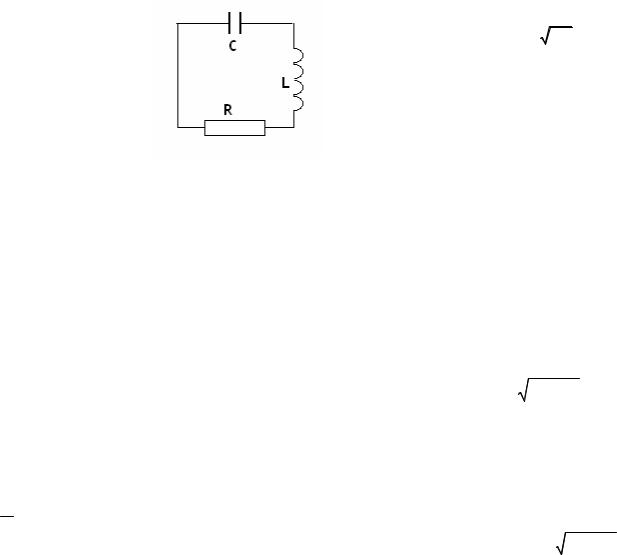

Скачиваний:

Добавлен:

10.06.2015

Размер:

194 Кб

Скачать

☆

Лабораторная работа №20.

«ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ»

Рассмотрим собственные колебания в контуре с сосредоточенными постоянными

емкостьюC ,

индуктивностью

сопротивлением R .

Будем считать, что электрические процессы в контуре квазистационарны. Это значит, что мгновенное значение тока i одно и то же в любом месте контура и что к мгновенным значениям электрических

величин можно применять правила Кирхгофа.

Согласно второму правилу Кирхгофа сумма напряжений в любом замкнутом контуре равна сумме ЭДС, встречающихся в этом контуре. В нашем случае

сумма напряжения на конденсаторе UC
UC =	q		(1)
UC =	C		(1)
	C
и на сопротивлении:
UR = iR			(2)
Равна ЭДС самоиндукции
εi = −L di			(3)
		dt

Которая возникает за счет изменения тока в катушке при перезарядке конденсатора.

UC +UR =εi	(4)
Используем определение силы тока:
i = dq	(5)
dt

Подставив (1), (2), (3), (5) в закон Кирхгофа (4), получим:

q + R dq = −L d 2q . C dt dt2

Разделим обе части этого уравнения на L и введем следующие обозначения:

	R	= β ,		(6)
	2L	= β ,		(6)
	2L
β - коэффициент затухания.
1			=ω2	(7)
			=ω2	(7)
	LC		0
	LC

ω0 - частота собственных колебаний контура ( при R = 0 ).

Получим стандартный вид дифференциального уравнения затухающих колебаний, описывающего изменение со временем заряда на обкладках

конденсатора в контуре RLC :

d 2 q		dq	2
	+ 2β		+ω0 q = 0	(8)
dt 2	+ 2β	dt	+ω0 q = 0	(8)
dt 2		dt

Это однородное линейное дифференциальное уравнение второго порядка с обыкновенными производными и с постоянными коэффициентами.

Решение этого уравнения имеет различный вид в зависимости от соотношения между коэффициентами. Положим сначала, что

ω02 > β 2 .
Тогда решение уравнения (8) имеет вид
q = q0e−βt cos (ωt +α),	(9)

q0 - заряд конденсатора в начальный момент времени, α начальная фаза. q0 и

α определяются из начальных условий. Из (9) следует, что заряд q (t) меняется

по закону косинуса, следовательно процесс перезарядки конденсатора является периодическим, происходящим с циклической частотой затухающих колебаний

ω = ω02 −β2

(10)

Множитель перед функцией косинуса убывает со временем по экспоненциальному закону и имеет смысл амплитуды затухающих колебаний:

A = q e−βt	(11)
0

Поэтому (9) есть затухающее колебание заряда на обкладках конденсатора, а (8) – соответствующее ему дифференциальное уравнение затухающих колнбаний, происходящее с периодом

T =	2π	=	2π
	ω		ω02 −β2

Подставив вместо ω0 и β их значения, получим

cosα < 0 , а

T =		2π			2π LC =T0	(12)
T =	1				2π LC =T0	(12)
	1		−	R2
	LC		−	2
	LC			4L

то есть период затухающих колебаний всегда больше периода собственных колебаний.

Разделив (9) на электроемкость C , получим напряжение на

конденсаторе:

e−β t cos (ωt +ϕ) =U0e−β t cos (ωt +ϕ)

(13)

Чтобы найти величину тока, продифференцируем (9) по времени:

i =

= q0 e−βt [− β cos(ωt +ϕ)−ωsin(ωt +ϕ)]

Умножим

разделим

это

выражение

на

ω2 + β 2

ω2

= ω

i = ω0 q0 e−βt −

cos(ωt +ϕ)−

sin(ωt +ϕ)

ω2 + β 2

Введем угол α , определяемый условиями:
cosα = −	β	=	−β , sinα =	ω	=	ω .

	ω2 +β2		ω0	ω2 + β 2		ω0

Тогда можно записать

i =ω0 q0 e

Поскольку

−βt cos(ωt +ϕ +α)			(14)
sin α > 0 ,	π	<α <π .
	2

Таким образом, при наличии в контуре активного сопротивления ток опережает по фазе напряжение на конденсаторе более, чем на π2 (при R = 0 на π2 ).

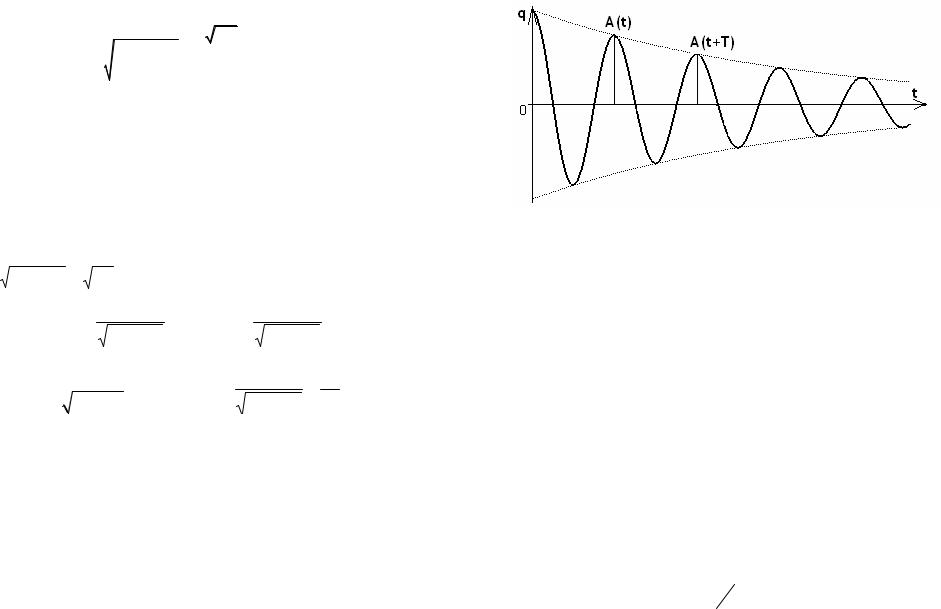
График функции (9) изображен на рисунке. Графики для напряжения и величины тока имеют аналогичный вид

Быстроту затухания колебаний наряду с коэффициентом затухания β

принято характеризировать еще логарифмическим декрементом затухания:

δ = ln

A(t )

(15)

A(t +T )

где A(t) - амплитуда соответствующей величины (q,U , i).

Подставив (11) в (15), получим:

δ = βT

(16)

Выясним

физический

смысл коэффициента

затуханияβ

логарифмического коэффициента затухания. Обозначим

через τ

время,

течении которого амплитуда колебаний уменьшается в e

раз. Это время τ

называют

временем

релаксации

системы.

Тогда

q0 exp(− β(t +τ))

= exp(− βτ )=

, а следовательно,

βτ =1

q0 exp(− βt)

(17)

Коэффициент затухания есть величина, обратная времени,							за которое амплитуда
колебаний уменьшается в e раз.
Подставив (17) в (16), получим
δ = βT =	1	T =	1		=	1	(18)
			τ			Ne
τ				T

Ne - число колебаний, происходящих за время τ .

Таким образом, логарифмический декремент есть величина, обратная числу колебаний, по истечению которых амплитуда уменьшается в e раз

(e = 2,72...).

Колебательный контур часто характеризуют добротностью Q , которая

определяется как величина, обратно пропорциональная логарифмическому декременту затухания

Q =	π	=πNe =	π	(19)

	δ		βT

Предположим теперь, что сопротивление контура велико, так что

ω0 < β .

В этом случае частота ω , выражаемая формулой (10), будет мнимой. Это значит, электрических колебаний в контуре не будет. В этом случае решение дифференциального уравнения имеет вид:

		q = A e−K1t + A e−K2t								(20)
		1				2
где K	1	= β + β 2 −ω2 ,		K	2	= β − β 2	−ω2	, а	A	и A
	1		0		2		0		1	2
постоянные, так как ω02			< β 2 , то K1 и K2				оба вещественны и положительны.

Значения постоянных определяются начальными условиями задачи:

t=0

= A + A = q

t=0

= −A K

− A K

= 0 .

Это дает

A1 = −q0

= q0

K1 − K2

после чего решение (20) принимает вид

q =

(K1e−K2t − K2 e−K1t ).

− K2

На рисунке

изображены

графически

оба

слагаемых этой формулы

(пунктир) и их

сумма

(сплошная

линия).

Вместо

колебаний

происходит

апериодический

разряд

конденсатора.

Если

сопротивление контура очень велико, так что β 2 >>ω02 , то K1 >> K2 и в последнем выражении можно пренебречь вторым слагаемым по сравнению с первым, а в знаменателе − K2 по сравнению с K1 . Тогда q = q0 e−K2t .

Из сказанного видно, что для возникновения колебаний в контуре RLC

необходимо,		чтобы выполнилось условие ω2				≥ β2		. Подставляем вместо β и
					0
ω0 их значения, находим условие возникновения колебаний в виде:
	1	>	R2	или	R ≤ 2		L	.
	LC	>	2	или	R ≤ 2		C	.
	LC		4L				C

Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим

			R	= 2	L	.

			кр		C

Электромеханическая аналогия.
Механическая система.						Электрическая система.
Пружинный маятник.						Колебательный контур.
Механические величин						Электрические величины
Смещение	X					Заряд конденсатора q
Масса груза	m					Индуктивность	I		1
Жесткость пружины K						Величина обратная эл. емк.
									C
Коэффициент трения				r		Сопротивление R

Скорость U =		dx				Величина тока	i =	dq
		dt						dt

Все формулы колебательных процессов электрической системы можно получить из соответствующих формул колебательных процессов механической системы указанными выше заменами величинами и наоборот.

Собственные затухающие колебания.
Механическая система с трением,	Электрический контур с
сила которого	сопротивлением

F		= −r dx	R
тр		dt
		dt
	Дифференциальное уравнение затухающих колебаний.
Второй закон Ньютона			Второе правило Кирхгофа

ma = Fтр + kx
m		d 2 x		= −r	dx	−kx
		dt 2			dt

d	2 x		+	r dx	+	k	x = 0

dt 2				m dt		m

Можно переписать в виде

εi =UR +Uc

−L d 2 q = R dq + 1 q dt 2 dt C

d 2 q	+	R dq	+	1	q = 0

dt 2		L dt		LC

d 2 x

+ 2β

+ω02 x = 0

d 2 q

+ 2β

+ω02 q = 0 ,

dt 2

где

= k

и коэффициент затухания

β =

Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего колебания затухают.

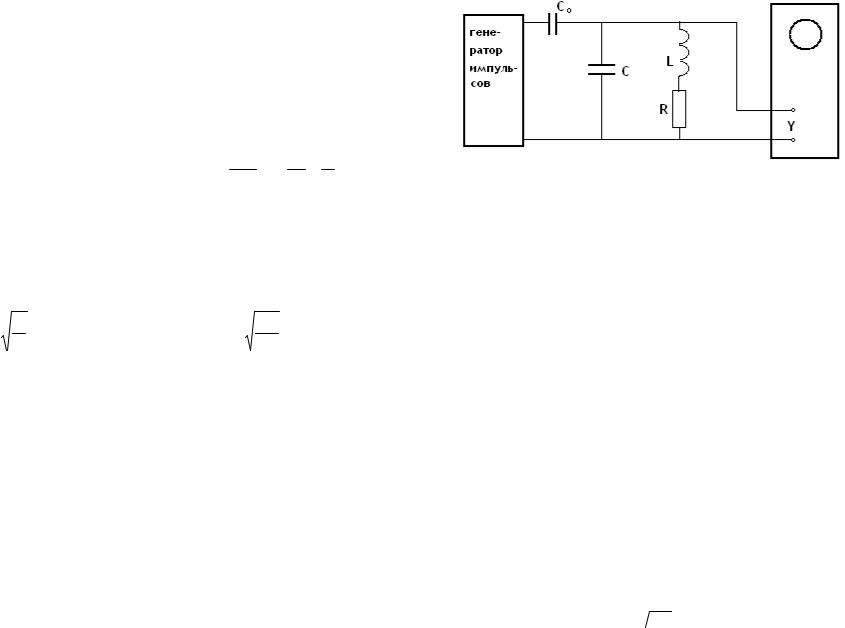
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ.

В работе исследуется свободные колебания в колебательном контуре. Блок–схемы измерительной установки изображены на рисунке.

Электроемкость C , индуктивность L и сопротивление R образуют колебательный контур. Колебания в контуре наблюдаются с помощью осциллографа. Для ударного возбуждения колебаний служит генератор

импульсов, соединенный с контуром через конденсатор C0 . Генератор

импульсов 50 раз в секунду вырабатывает короткие импульсы.

Конденсатор контура получает некоторый начальный заряд. В промежутках между импульсами в контуре совершаются свободные колебания, описываемые уравнением (1).

ВЫПОЛНЕНИЕ РАБОТЫ И ОБРАБОТКА РЕЗУЛЬТАТОВ.

1. Включить макет и осциллограф.. Установить значения

L =100(мГн) , C =1(мкФ) , R = 0(Ом) .

(учитывая, что к величине R всегда добавляется сопротивление катушки R0 ).

2. С помощью ручки осциллографа «время/деление» «остановить» картину колебаний на экране осциллографа.

3. Ручку «развертка» установить на 1 – 2 мкс, (так, чтобы на экране осциллографа помещалось 3 – 4 полных колебания). Ручка «развертка плавно» должна находиться в выключенном положении.

4. С помощью осциллографа измерить период затухающих колебаний. 5.Измерения следует проделать для 3 – 5 различных значений C при постоянной L (емкость изменять переключателем «×0,1» в пределах от 0,1 до 1 мкФ). Затем 3 - 5 раз меняя L при постоянной C (индуктивность изменять переключателем «×10» в пределах от 10 до 100 мГн) .

6. Сравнить измеренные значения периода колебаний с вычисленным по приближенной формуле

T = 2π LC

и по точной	2π		2π			2π
T =	2π	=	2π	=		2π	.
	ω		ω02 − β 2	1			R 2
						−
					LC	−
					LC		2L

7. Определение критического сопротивления.

Постепенно увеличивая включенное в колебательный контур сопротивление R (переключателем «×100»), следует наблюдать за возрастанием скорости затухания колебаний и проследить переход из колебательной формы разряда в

апериодическим. Определить критическое сопротивление Rкр . Сравнить это

значение с вычисленным из условия β =ω0 .

8. Определение логарифмического декремента затухания и добротности контура. Исследовать зависимость логарифмического декремента затухания и

добротности контура от величины R при неизменных значениях C и L (учитывая, что к величине R всегда добавляется сопротивление катушки R0 ). Для этого на экране осциллографа, пользуясь миллиметровой бумагой, измеряют две амплитуды, отстоящие на N периодов. Затем из выражения

			A(t)		q0e−β t
	ln			= ln		= NβT = Nδ
			A(t + NT )		q0e−β (t+NT )
вычисляют δ и добротность Q
	ln		A(t)
δ =		A(t + NT )			Q =		π	.
			N				δ

Полученные результаты сравнить с теоретическими, расчет производить по

формуле для добротности

Q = πδ = 2RTπL

и логарифмического декремента

δ = βT = RT2L .

Результаты измерений записать в следующую таблицу

№

T = 2π LC

T =

2π

п/п

−

кр

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1.Выведите дифференциальное уравнение затухающих колебаний в CLR – контуре.

2.Запишите и проанализируйте решение дифференциального уравнения затухающих колебаний.

3.Запишите и проанализируйте формулу циклической частоты затухающих колебаний.

4.Запишите формулу периода затухающих колебаний в контуре.

5.При каком условии колебания становятся апериодическими? Какое сопротивление называется критическим? Какие процессы происходят при этом в контуре?

6.Объясните физический смысл коэффициента затухания.

7.Какая величина называется логарифмическим декрементом затухания? Каков его физический смысл?

8.Дайте определение добротности.

9.Запишите функции зависимости заряда и напряжения на конденсаторе, силы тока в контуре от времени.

Соседние файлы в папке лабораторные работы

#
10.06.2015198.89 Кб87lab12.pdf
#
10.06.2015269.62 Кб81lab13.pdf
#
10.06.2015198.88 Кб84lab17.pdf
#
10.06.2015194 Кб77lab20.pdf
#
10.06.2015629.29 Кб78lab31-32-33-39-48.pdf
#
10.06.2015204.96 Кб78lab35-42.pdf
#
10.06.2015164.64 Кб81lab41-47.pdf
#
10.06.2015125.77 Кб75lab61.pdf
#
10.06.2015173.5 Кб77lab66.pdf