Курсовая работа / Вариант 3 - Faz - 2006 / kurs_fa

Российский Химико-Технологический Университет им. Д.И. Менделеева

Курсовая работа по основам стандартизации и метрологии.

Статистическая обработка экспериментальных данных при сертификации продукции

Оценка распределений их параметров

Вариант: 3

Выполнил: студент Гр О 41

Faz Birmutt

www.PXTY.info

Москва 2006

В ста случаях зарегистрировано время проведения синтеза на химическом производстве.

Результаты регистрации сведены в таблицу:

27	51	107	21	20	46	35	27	6	25
16	118	3	3	0	54	85	30	39	43
15	59	3	143	70	100	82	71	64	67
17	29	43	285	3	17	185	42	26	3
88	22	31	6	25	0	29	170	242	22
31	79	117	0	101	55	32	38	13	16
42	316	0	32	52	102	7	63	24	68
67	29	17	4	21	96	112	91	26	9
167	7	58	132	21	20	28	0	5	26
20	58	65	96	19	42	99	30	79	65

Содержание работы:

1) Используя табличные значения необходимо найти математическое ожидание и дисперсию случайной величины Х.

2) Найти доверительные интервалы для математического ожидания и дисперсии, соответствующие доверительной вероятности (1-a) = 0,95.

3) Оценить вероятность попадания случайной величины Х в интервал (0,7..1).

4) Для этой вероятности найти доверительный интервал, соответствующий коэффициенту доверия (1-а) = 0,9.

5) Построить гистограмму и эмпирическую функцию распределения случайной величины Х.

6) Найти и построить доверительные области для плотности распределения соответствующую коэффициенту доверия (1-а) = 0,95 и функции распределения , соответствующую коэффициенту доверия (1-а) = 0,8.

7) Сгладить гистограмму и эмпирическую функцию распределения подходящим законом распределения.

8) Используя критерии согласия и Колмогорова проверить правдоподобие гипотезы о совпадении выбранного закона распределения с истинным законом при уровне значимости а = 0,1.

1. Находим точечные оценки математического ожидания и дисперсии, учитывая, что n = 100.

= 54,12

= 3289,844

= 3256,946

2. Рассчитываем доверительные интервалы для математического ожидания и дисперсии. По формуле:

= 0,475

и таблице значений функции Лапласа находим:

и, следовательно, искомые доверительные интервалы будут иметь вид:

3. Находим точечную оценку вероятности попадания случайной величины Х в интервал . Т.к. в этот интервал попало m = 11 экспериментальных значений, то искомая оценка будет равна:

= 0,11

4. Рассчитываем доверительный интервал для вероятности Р, оцененной в предыдущем пункте.

искомый интервал имеет вид:

5. Для построения гистограммы заключаем все экспериментальные данные в интервал (0,320) и разбиваем его на 10 равных разрядов, каждый длиной 32. Затем рассчитываем следующую таблицу.

Частоты попадания экспериментальных точек в разряды гистограммы:

Значение гистограммы:

Г(x)=

разряд	1	2	3	4	5	6	7	8	9	10
0	32	64	96	128	160	192	224	256	288	320
точек	49	19	14	10	2	3	0	1	1	1
частота	0,49	0,19	0,14	0,1	0,02	0,03	0	0,01	0,01	0,01
Г(х)	0,015	0,006	0,004	0,003	6E-04	9E-04	0	3E-04	3E-04	3E-04

6. Доверительные области для плотности распределения и функции распределения .

В данном случае общее число разрядов r равно 10 плюс один полубесконечный разряд, т.е.r = 11.

По формуле:

= 0,4977

из таблицы получим .

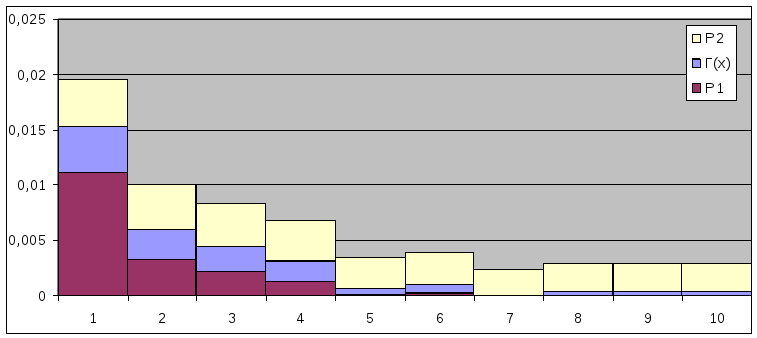
Результирующие доверительные границы для плотности на каждом разряде гистограммы представлены в таблице:

где ,

разряд	1	2	3	4	5	6	7	8	9	10
0	32	64	96	128	160	192	224	256	288	320
P	0,354	0,103	0,068	0,043	0,003	0,007	0	0,001	0,001	0,001
	0,627	0,323	0,265	0,217	0,108	0,123	0,075	0,092	0,092	0,092
f	0,011	0,003	0,002	0,001	1E-04	2E-04	0	3E-05	3E-05	3E-05
	0,02	0,01	0,008	0,007	0,003	0,004	0,002	0,003	0,003	0,003

График гистограммы.

Графической оценкой функции распределения является эмпирическая функция распределения:

, где – число экспериментальных точек, лежащих левее

#	1	2	3	4	5	6	7	8	9	10
0	32	64	96	128	160	192	224	256	288	320
nx	0	49	68	82	92	94	97	97	98	99
F	0	0,49	0,68	0,82	0,92	0,94	0,97	0,97	0,98	0,99

Далее по таблице распределения величины (распределение Колмогорова) находим ее величину, соответствующую заданному коэффициенту доверия. Она равна = 1,08.

Затем рассчитываем доверительную область для функции распределения :

, где , = 0,11

#	1	2	3	4	5	6	7	8	9	10
0	32	64	96	128	160	192	224	256	288	320
F	-0,1	0,38	0,57	0,71	0,81	0,83	0,86	0,86	0,87	0,88
	0,11	0,6	0,79	0,93	1,03	1,05	1,08	1,08	1,09	1,1

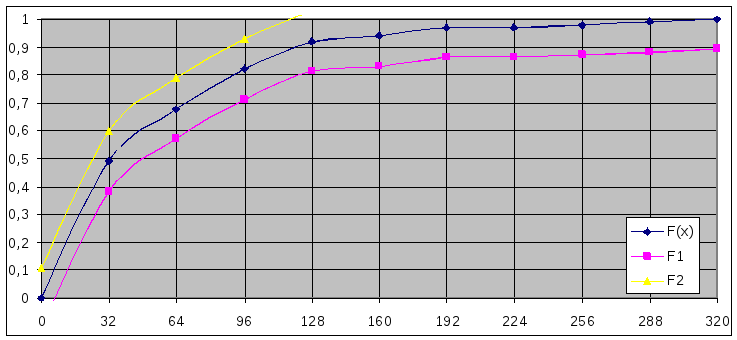
График этой области:

7. Из формы гистограммы следует, что гипотетическим распределением может быть экспоненциальное распределение с функцией:

и с плотностью

где - оценка неизвестного истинного значения. Т.к. , то и, следовательно,

#	1	2	3	4	5	6	7	8	9	10
0	32	64	96	128	160	192	224	256	288	320
Fг	0	0,45	0,69	0,83	0,91	0,95	0,97	0,98	0,99	1
fг	0,02	0,01	0,01	0	0	0	0	0	0	0

8. Для проверки гипотезы используем вначале критерий согласия. Его экспериментальное значение, согласно формуле:

= 9,29

А его гипотетическое значение при заданном уровне значимости и числе степеней свободы s = 11 - 1 - 1 = 9, согласно условию , равно . Таким образом, и, следовательно, гипотеза по критерию согласия является правдоподобной.

Теперь проверим ту же самую гипотезу с помощью критерия согласия Колмогорова. Максимальное различие между гипотетической и эмпирической функциями распределения в этом случае равно:

= 0,04

откуда получаем экспериментальное значение критерия Колмогорова:

Гипотетическое значение того же самого критерия при заданном уровне равно . Таким образом, и, следовательно, гипотеза является правдоподобной также и по критерию Колмогорова.