для первого курса / для первого курса / Ответы по вышке / Ответы по вышке / интегралы / 03. Определенный интеграл

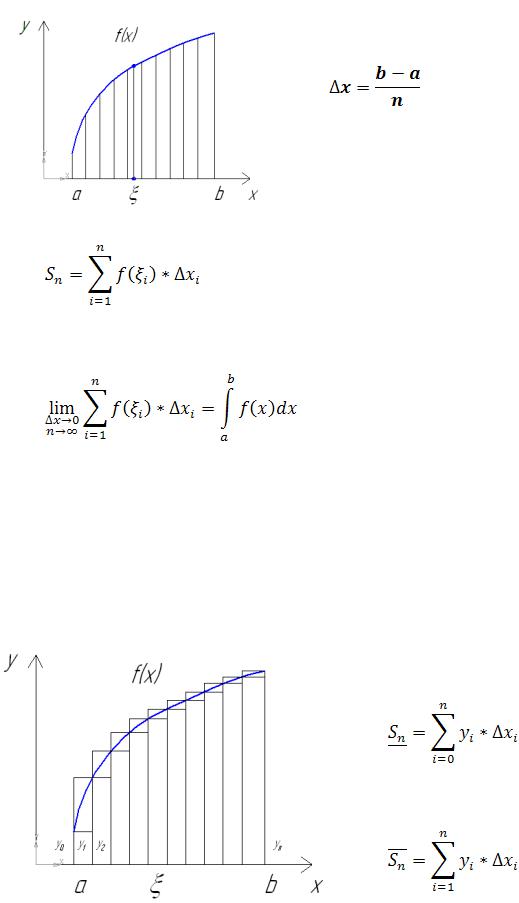
Определенный интеграл.

1. Понятие определенного интеграла как представление интегральной суммы.

Пусть f(x) C[a:b]-не прерывный на отрезке ab и f(x)≥0.

Площадь фигуры ограниченной прямыми y=f(x); y=0; x=a; x=b. Разделим отрезок ab на n

частей и проведем прямые.

На каждом из таких отрезков поставим точки ξI и вычислим значение в этой функции y=f(ξI) и вычислим площадь малого отрезка, которая будет равной Si= f(ξI)*∆xi Если мы в каждом отрезке возьмем такую точку и найдем их

площадь и затем просуммируем эти площади то получим (1).

Для получения более точной площади необходимо увеличивать число n до бесконечности.

Перейдем от выражения к пределу при ∆x→0 и n→∞ то получим (2).

(1)– Интегральная сумма.

(2)– предел интегральной суммы , называемый определенным интегралом.

Где а – нижний предел интегрирования. b – верхний предел интегрирования.

f(x) – под интегральная сумма dx – дифференциал. f(x)dx – под интегральное выражение.

С помощью определенного интеграла можно вычислить площадь плоских

фигур, объемных тел, работу, массу, величину электрического заряда и т.д.

Нижний интеграл (3) площадь фигуры меньше реальной фигуры.

Верхний интеграл (4) площадь фигуры больше реальной площади фигуры.

Переход к пределу выражений 3 и 4

получим определенный интеграл.

Свойства.

Определенный интеграл является линейным функционалом и для него существуют основные 2 свойства свойствами функционалами.

1.Постоянное множество вынести за знак определенного интеграла.

2.Определенный интеграл от суммы равен сумме интегралов от этих интегралов.

Доказательные свойства 1 и 2 основано на свойстве сумм.

3.При изменении порядка интегрирования интеграл меняет знак на противоположный.

4.Интеграл от одного участка интегрирования равен 0

5.С (ab)

Свойства определенных интегралов выраженных неравенством. (Оценка определенного интеграла).

Теорема 1. Если а>b а f(x)≥0 то интеграл больше или равен 0.

Теорема 2. Если а <b, а f(x)≤g(x) то

Теорема 3. Если а <b, а m≤f(x)≤М где m-min f(x); M-max f(x) на отрезке (а

b)то

Теорема 4. Если а <b,

Теорема 1-4 показывает что неравенства можно интегрировать.

Теорема о среднем значении. Введем понятия среднего значения. f(x) c[ab]; разобьем отрезок на n

частей.

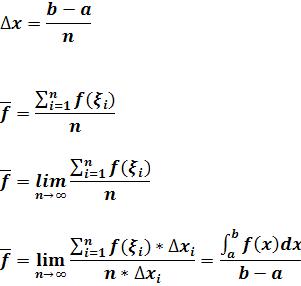
Выберем точку кси и вычислим значение функции в ней. Возьмем множество таких точек и найдем их сумму и разделим на n.

Переходя от выражения к пределу мы получим среднее значения.

Умножим числитель и знаменатель на ∆xi.

Средне значение.

Теорема ( о среднем значении). Если f(x) c[ab] то существует такая точка кси [ab] в которой 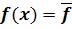.