
для первого курса / для первого курса / Ответы по вышке / Ответы по вышке / интегралы / 05. Не собственный интеграл
.pdf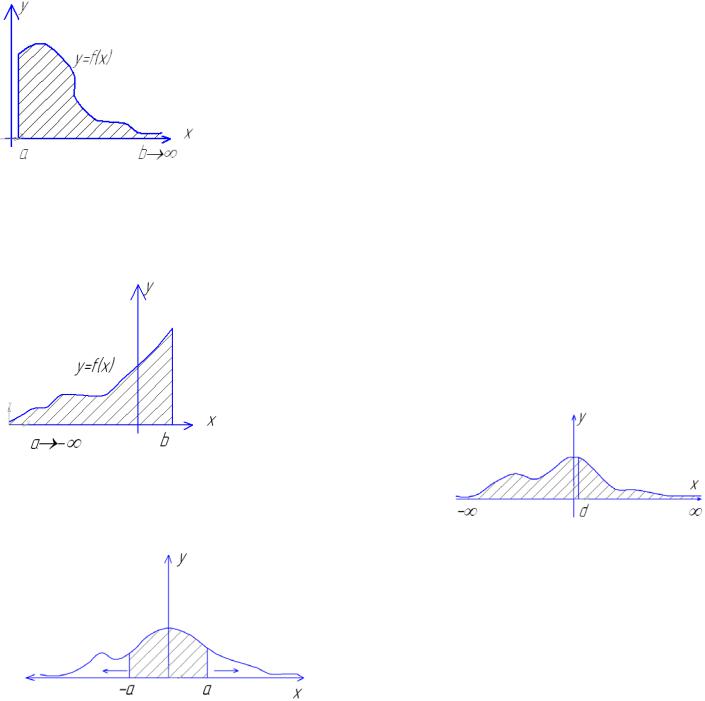
Не собственный интеграл. |
∫ |
|
|
|
|
|
При изучении определенного интеграла |
|
( |
) |
|
предполагалось, что: |
|
1. |
Промежуток интеграла конечный. |
|
|
|
|
|
2. |
f(x) C[a;b] |
|
|
|
|
|
Если нарушается хоть одно из условий то интеграл будет не собственным.
1.Не собственный интеграл с бесконечным пределом интегрирования.
(не собственный интеграл 1 рода) Пусть бесконечный предел будет верхний |
||||
∞ |
→∞ |
|
|
|
|
|
|
||
предел f(x) [a;∞] и тогда равенства (1) |
|
( |
) |
|
|
f(x)dx = blim |
|||
Геометрический смысл этого интеграла. Несобственный интеграл при b стремящегося к
бесконечности определяется площадью бесконечной фигурой. Предел в правой части равенства (1), может быть конечным. Говорят что несобственный интеграл сходиться если существует конечных предел в правой части равенства (1). Если не существует конечный предел в правой части равенства (1) то несобственный интеграл расходиться. Аналогично можно определить
несобственный интеграл 1 рода с бесконечно нижним пределом, в этом случае |
||||||||||||||||||
f(x) [-∞;b] и тогда равенство (2) |
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|||
− |
|
f(x)dx = alim |
|
|
|
|
||||||||||||
|
|
|
|
|
( |
) |
|
|
|
|||||||||
|
∞ |
|
|
|
|
→− |
|
|
|
|
|
|
|
|
|
|
||
|
|
←Геометрический смысл. |
||||||||||||||||
|
|
Если рассмотреть f(x) [- ∞;∞], то разобьем на |
||||||||||||||||
2 участка точкой d принадлежавшей этому участку |
||||||||||||||||||
|
|
∫ |
|
|
|
( |
|
) |
|
|
= |
∫ |
|
|
∫ |
|
||
|
|
− |
|
|
|
|
|
|
|
|
− f(x)dx + |
f(x)dx |
||||||
|
|
|
∞∞ |
|
|
|
|
|
|
|
|
|
|
∞ |
|
∞ |
||
и получим (3) |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Геометрический смысл. |
|
|||||||||||||||
|
|
d |
|
|
|
– |
|
|
|
|
любая |
|
|
|||||
промежуточная |
|
точка |
|
|
||||||||||||||
и |
|
от |
|
выбора |
|
этой |
|
|
||||||||||
точки значение интеграла не зависит.
Интеграл (3) сходиться тогда и только тогда когда оба интеграла в правой части уравнения (3)
сходятся, если хотя бы 1 из них расходятся, то интеграл слева расходится. Введем понятия главного значения не
собственного интеграла 1 рода. |
|
||
+∞ |
|
|
|
V.p – главное значение.(4) |
|
||
|
( ) = ( ) |
|
|
−∞ |
− |
что |
не |
Может |
оказаться, |
||
собственный интеграл не существует, но при -а→- ∞ и а→∞ может получится сходящимся интегралом. Дело в том, если функция f(x) является нечетной, то ёё интегралом [-a;a] в симметричном промежутке равняется нулю, то есть главная часть от симметричной функции
будет всегда равняться нулю, хотя не собственный интегралом может совсем не существовать. Для четной функции главная часть существует, если существует несобственный интеграл.
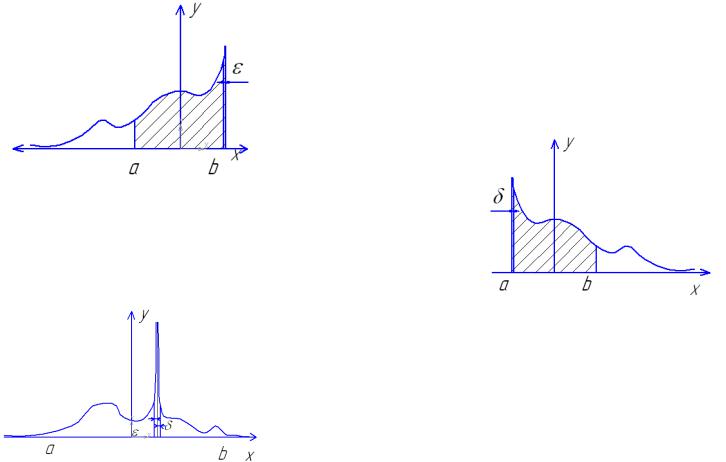
Рассмотрим несобственный интеграл 2 рода, |
то есть от функции имеющих |
|||||||||||||||||||||
разрыв внутри промежутка интегрирования, то есть нарушается условие 2. |
||||||||||||||||||||||
Рассмотрим интеграл |
у |
которого |
разрыв функции иметься в верхнем |
|||||||||||||||||||
|
|
|
|
∫ |
|
|
|
|
= lim |
|
∫ |
− |
|
|
|
|
|
|
||||
пределе. |
|
|
|
|
|
|
( |
) |
|
|
|
|
→0 |
|
( |
|
) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
= |
( ) − 2 рода |
||||||||||
|
|
|
|
Сходящийся , если сходящийся придел в |
||||||||||||||||||
|
|
|
правой части, если он равен бесконечности. |
|||||||||||||||||||
|
|
|
|
Если предел функции имеется в нижней части |
||||||||||||||||||
|
→0 |
функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
( ) = lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим функции непрерывную на отрезке |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
[a;b] |
|
|
|
|
|
( ) |
[ , ], [ , ] т. р. 2 рода. |
||||||||||||
|
|
|
|
( ) |
= |
|
( ) + |
( ) |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
→0 |
− |
|
|
|
|
|
|
→0 |
|||
|
|
|
|
|
|
|
|
|
|
= lim |
|
( ) |
+ lim |
( ) (7) |
||||||||
Главный значение для |
несобственных |
интегралов |
|
2 |
рода вводится |
|||||||||||||||||
|
|
+ |
||||||||||||||||||||
|
|
|
→0 − |
|
|
|
|
|
|
→0 |
|
|
|
|
|
|
|
|
|
|
||
аналогичным образом как и для 1 рода. |
|
|
|
|
|
|
( ) (8) |
|
||||||||||||||
|
( ) |
= lim |
|
( ) + lim |
|
|
||||||||||||||||
В случае вычисления |
несобственного |
интеграла 2 рода с точкой разрыва |
||||||||||||||||||||
|
|
+ |
|
|
|
|
|
|
|
|
||||||||||||
внутри промежутка интегрирования в общем случае пределы вычисляются при разных значениях ε и δ. В случае главного значения эти промежутки должны быть симметричны. Если сходиться интеграл (7), то и (8) сходится. Как вычислить
несобственный интеграл 1 рода, если подынтегральная функция имеет разрыв 1
рода виде скачка? ( ) = ( ) + ( )
Основные свойства интегралов, аналогичны свойствам определенных интегралов.
Теоремы о схождении несобственных интегралов.

Вопрос о сходимости несобственного интеграла в ряде случаев можно решить без его вычисления. Это особенно важно когда нельзя выразить первообразную через элементарную функцию.
Рассмотрим теоремы о сходимости несобственных интегралов 1 рода. Теорема 1. Если f(x) и g(x) C[a,b] и при этом g(x)≥ f(x)≥0 то интеграл от
g(x) сходиться, если сходится интеграл от f(x). Если при тех же предположениях интеграл от f(x) расходится то и следовательно( ) g(x) тоже расходится. ∫ | ( )|
Теорема 2. Если сходящийся∫ интеграл от абсолютной величины следовательно сходится и . И в этом случае интеграл называется
абсолютно сходящимся.
Встречаются случаи когда интеграл по модулю расходится, а интеграл без модуля сходится.
Теорема 3. Если обе функции f(x) и |
g(x) C[a,b] |
и существует конечный не |
|||||||||||||||
|
|
|
∫ |
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
нулей предел отражения этих функции. |
|
|
|
|
|||||||||||||
То в этом случае |
|
|
∞ |
|
|
|
|
и |
|
∞ |
|
|
либо сходится либо расходится. |
||||
Поскольку в практике очень( часто) |
|
рассматриваются( ) |
степенные интегралы, то |
||||||||||||||
часто выполняют |
сравнения |
искомого интеграла с интегралом от степенной |
|||||||||||||||
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
> 1 →← |
|
|||
функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
→ ≤ 1 ←→ |
|
||||||||
Аналогичные |
теоремы |
|
|
||||||||||||||
|
|
|
|
|
|
|
можно сформулировать и для несобственных |
||||||||||
интегралов второго рода, сравнение в |
этом случае производит так же со |
||||||||||||||||
|
|
|
|
|
|
|
разрыв вточкеи < 1 →← |
||||||||||
степенными интегралами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
( |
− ) |
|
|
разрыв вточке ≥ 1 ←→ |
|||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
( − ) |
|
|
|
|
|
|
|
|
|
|
||||
