
Аналитическая геометрия - В.М. Гордиенко / Lecture 1-2
.pdf
Лекция 2
Начинаем изучать векторные пространства. У нас должны появиться понятия:
Xбазис векторного пространства
Xразмерность векторного пространства
Xкоординаты вектора
() |
Лекция 2 |
10 сентября 2011 г. |
1 / 28 |

Векторы линейно зависимые и линейно не зависимые
Три ненулевых радиус-вектора могут располагаться в пространстве различными способами:
они могут не лежать в одной плоскости (векторы a; c; d) ;
они могут лежать в одной плоскости (векторы a; b; c) ;
и могут лежать на одной прямой.
Мы хотим формализовать это понятие. Т.е., мы хотим сформулировать его для произвольного (абстрактного) линейного пространства.
() |
Лекция 2 |
10 сентября 2011 г. |
2 / 28 |

Например, рассмотрим в трёхмерном пространстве R3 следующие три вектора:
a1 |
= |
223 |
, |
a2 |
= |
233 |
, |
a3 |
= |
2123. |
|
|
1 |
|
|
|
4 |
|
|
|
11 |
|
|
435 |
|
|
|
425 |
|
|
|
4135 |
Лежат ли эти три вектора в одной плоскости ? Что означает, что они лежат в одной плоскости ?
() |
Лекция 2 |
10 сентября 2011 г. |
3 / 28 |

Ещё один пример, рассмотрим в пространстве полиномов следующие три полинома:
P1(t) = t3 3t2 + 4t + 5 ;
P2(t) = 3t2 t 2 ;
P3(t) = t3 + 3t2 + 2t + 1 :
Лежат ли эти три полинома в одной плоскости ? Что означает, что они лежат в одной плоскости ?
Те же вопросы в случае матриц |
|
|
|
3 |
6 |
|
||||||||
A1 |
= |
6 |
3 |
; |
A2 |
= |
3 |
0 |
; |
A3 |
= |
: |
||
|
|
5 |
4 |
|
|
|
2 |
2 |
|
|
|
4 |
2 |
|
Лежат ли эти три матрицы в одной плоскости ?
Что означает, что они лежат в одной плоскости ?
() |
Лекция 2 |
10 сентября 2011 г. |
4 / 28 |

Пусть V векторное пространство, и
a1; a2; : : : ; am 2 V.
Мы можем эти векторы сложить, предварительно умножив
каждый на число |
j , получим некоторый вектор |
|
a = 1a1 + 2a2 + : : : + mam ; |
||
|
m |
|
a = |
jX |
(краткая запись того же). |
jaj |
||
|
=1 |
|
Вектор a называется линейной комбинацией векторов
a1; a2; : : : ; am с коэффициентами 1; 2; : : : ; m .
Говорят также, что вектор a линейно выражается
через векторы a1; a2; : : : ; am .
() |
Лекция 2 |
10 сентября 2011 г. |
5 / 28 |

Если 8j |
j = 0 , то линейная комбинация |
|
a = 1a1 + 2a2 + : : : + mam |
|
|
называется |
тривиальной, в этом случае всегда a = 0 . |
|
Это понятно и здесь больше нечего обсуждать. |
||
Поэтому мы, как правило, будем рассматривать |
||
нетривиальные линейные комбинации |
|
|
a = 1a1 + 2a2 + : : : + mam |
9 j0 6= 0 . |
|
() |
Лекция 2 |
10 сентября 2011 г. |
6 / 28 |

Итак, пусть V векторное пространство, и
a1; a2; : : : ; am 2 V.
Рассматриваются всевозможные нетривиальные линейные комбинации
m |
|
jX |
9 j0 6= 0 . |
a = jaj |
|
=1 |
|
Будем различать две ситуации:
() |
Лекция 2 |
10 сентября 2011 г. |
7 / 28 |

выполняется |
|
9 |
|
j0 |
6 |
|
|
I: При некоторой нетривиальной линейной комбинации |
|
|
|
= 0 |
|
||
m |
|
|
|
|
|
|
|
jX |
1a1 + 2a2 + : : : + mam = 0 . |
|
|
|
|
||
jaj = 0 ; |
|
|
|
|
|||
=1 |
|
|
|
|
|
|
|
В этом случае векторы a1; a2; : : : ; am называются |
|
|
|
|
|
|
|
линейно зависимыми. |
9 |
|
|
|
|
|
|
выполняется |
|
j0 |
6 |
|
|||
II: При любой нетривиальной линейной комбинации |
|
|
= 0 |
|
|||
m
X
jaj 6= 0 .
j=1
В этом случае векторы a1; a2; : : : ; am называются линейно независимыми.
() |
Лекция 2 |
10 сентября 2011 г. |
8 / 28 |
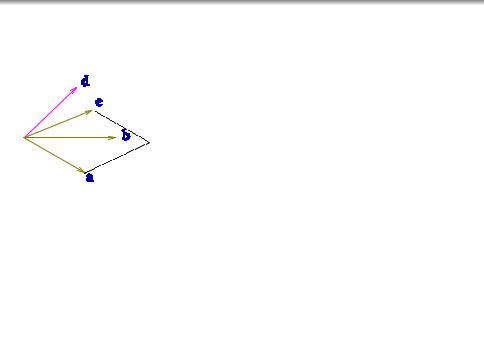
векторы a; b; c линейно зависимы,
а векторы a; c; d линейно независимы
Приведём эквивалентные формулировки понятий линейной зависимости и линейной независимости.
() |
Лекция 2 |
10 сентября 2011 г. |
9 / 28 |

Утверждение
Векторы a1; a2; : : : ; am 2 V линейно зависимы () некоторый из них aj0 линейно выражается через остальные
m
X
aj0 = jaj .
j=1; j6=j0
J =) Пусть 1a1 + 2a2 + : : : + j0 aj0 + : : : + mam = 0 ;
m
X
j0 6= 0 ; |
|
j0 aj0 = |
jaj , |
|
|
|
||
|
|
|
|
j=1; j6=j0 |
|
|
|
|
|
m |
jj0 aj , |
j = jj0 . |
|||||
aj0 = j=1; j=j0 |
||||||||
|
X6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратно |
(= |
|
|
|
|
|
|
|
|
m |
|
|
m |
|
|
|
|
j=1X; j6=j0 |
|
|
jX |
|
|
|||
aj0 = |
jaj |
! |
jaj = 0 |
j0 = 1 . I |
||||
|
|
|
=1 |
|
|
|
|
|
() |
Лекция 2 |
10 сентября 2011 г. |
10 / 28 |
