dsd13-gos / dsd-17=dacs and adcs / 12. Дельта-сигма модулятор

Лекция 12. Дельта-сигма модулятор.

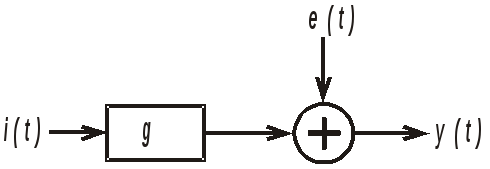
Базовая структурная схема  модулятора представлена на рис. 12.1, а; линейная модель квантователя на рис. 12.1, б. В простейшем случае для  модулятора первого порядка H(z) является передаточной функцией интегратора

,

тогда .

а) б)

Рис. 12.1.  модулятор: а – базовая структурная схема; б – линейная модель квантователя

В качестве блока H(z) может быть использован каскад интеграторов на переключаемых конденсаторах, в качестве квантователя и ЦАП обычно применяется двухуровневый компаратор и переключатель соответственно.

Типовая структурная схема  модулятора первого порядка приведена на рис. 12.2.

Рис. 12.2. Структурная схема  модулятора первого порядка

Рис. 12.3. Структурная схема  модулятора второго порядка

Рис. 12.4. Структурная схема  модулятора L–го порядка

Спектральная плотность мощности шумов квантования в общем случае

,

где ∆ – разность уровней квантователя.

Мощность шумов квантования в полосе частот сигнала при избыточной дискретизации

,

где – коэффициент избыточной дискретизации (передискретизации); – частота Найквиста.

В соответствии с передаточной функцией шумов квантования  модулятора первого порядка спектральная плотность мощности шумов квантования для  модулятора имеет вид

,

и мощность шумов квантования в полосе частот сигнала

, .

Динамический диапазон  модулятора первого порядка

,

Типовой модулятор второго порядка изображен на рис. 12.3.

Передаточная функция (при a₁ = b₁ = с₂ = 1, a₂ = 2)

.

Спектральная плотность мощности шумов квантования

.

Мощность шумов квантования в полосе частот сигнала

, .

Соответственно для модуляторов порядка L с простой обратной связью (рис. 12.4) верны следующие соотношения

,

,

, .

Для определения эффективного количества бит  модулятора можно использовать выражение

,

где b – разрешение внутреннего квантователя.

 модулятор первого порядка с однофазным входом

В схеме (рис. 12.5)  модулятора первого порядка с однофазным входом минимальное количество ключей. В такой схеме одинаковые весовые коэффициенты в цепи входного сигнала и обратной связи. Компаратор защелкивается по срезу сигнала φ₂ и его выход сохраняется неизменным до следующего переключения.

Рис. 12.5. Схема электрическая  модулятора первого порядка с однофазным входом

 модулятор второго порядка с парафазным входом

На рис. 12.6 приведена схема  модулятора второго порядка с парафазным входом. Возможные весовые коэффициенты a₁ = a₂ = b₁ = c₂ = 0,5, или, например, a₁ = b₁ = a₂ = 0,25 и c₂ = 0,5. В обоих случаях соблюдается условие стабильности . В схемах различаются входные уровни ОУ. Для уменьшения влияния смещения нуля и низкочастотных шумов используется техника «чоппер–стабилизации».

Временная диаграмма переключающих сигналов приведена на рис. 12.7. Для устранения зависимости инжекции зарядов от уровня сигналов, фазы одноименных ключей (φ₁, φ₂ и φ_1d, φ_2d) сдвинуты относительно друг друга на величину t_d.

Рис. 12.6. Схема электрическая  модулятора второго порядка с парафазным входом

Рис. 12.7. Временная диаграмма переключающих сигналов

 модулятора третьего порядка с парафазным входом

Для реализации дельта–сигма модулятора третьего порядка выбрана структура с использованием каскада интеграторов (рис. 12.8).

Рис. 12.8. Дельта-сигма модулятор третьего порядка с использованием каскада интеграторов

С учетом ограничений накладываемых на амплитудное значение передаточной функции для обеспечения стабильности модулятора, передаточная функция ФВЧ формирования шумов квантования может быть выбрана на основе приближения Баттерворта

.

Расположение нулей в точке z = 1 обеспечивает возможность выбора коэффициента избыточной дискретизации в широком диапазоне.

Передаточная функция звена интеграторов при c₂ = c₃ = 1 и b₁ = a₁

В этом случае b₁ = 0,0232; c₂ = 1,0; c₃ = 1,0; a₁ = 0,0232; a₂ = 0,1348; a₃ = 0,4679. Или, после масштабирования с целью оптимизации выходных напряжений каскадов: b₁^' = 0,1847; c₂^' = 0,2459; c₃^' = 0,5108; a₁^' = 0,1847; a₂^' = 0,2639; a₃^' = 0,4679.

Схема электрическая  модулятора третьего порядка с парафазным входом приведена на рис. 12.9.

Рис. 12.9. Схема электрическая  модулятора третьего порядка с парафазным входом

При проектировании реального АЦП необходимо учитывать неидеальности внутренних узлов  модулятора (табл. 12.1).

Факторы, влияющие на характеристики  модулятора

Т а б л и ц а 12.1. Факторы, влияющие на характеристики  модулятора

Факторы, влияющие на характеристики  модулятора	Пояснения
1	2
Нестабильность  модулятора	Нестабильность вызвана перегрузкой выводов внутренних блоков. Моду-лятор первого порядка (рис. 12.2) для входного сигнала в диапазоне – стабилен. Стабильность модулятора второго порядка (рис. 12.3) для входного сигнала в диапазоне обеспечивается при
Наличие паузных комбинаций	Характеристики  модулятора обычно рассчитываются на основе источника белого шума, моделирующего ошибки квантования. В действительности, в выходных сигналах модулятора появляются повторяющиеся последовательности, частота которых при определенных уровнях входного сигнала может лежать в рабочей полосе. Таким образом, шум квантования не является белым и может значительно превышать теоретически предсказанный. Одним из способов решения проблемы является подмешивание псевдослучайного сигнала
Конечный коэффициент усиления ОУ	Коэффициент усиления ОУ КуU должен удовлетворять следующему соотношению: . Обычно считают достаточным удвоенное значение коэффициента избыточной дискретизации
Неидеальности блоков  модулятора ОУ (конечный коэффициент усиления, ограниченная скорость нарастания, конечная полоса пропускания, ограниченный размах выходного сигнала, шумы), ключей (конечное сопротивление, помехи	Неидеальности приводят к увеличению шумов, нелинейности, гармоническим искажениям, перегрузке
“пролезания”), конденсаторов (нелинейность, рассогласование) компараторов
Нелинейность выходных сигна-лов двухуровневого ЦАП	Среднее значение выхода формата NRZ (без возврата к “0”) двухуров-невого ЦАП нелинейно относительно входного кода. Линейность достигается, например, использованием Формата RTZ (с возвратом к “0”). Данный тип нелинейности является существенным при применении аналоговых интеграторов (непрерывного действия).
Фазовый шум сигналов тактирования, шум по шинам “земля” и “питание”.	Увеличение шумов модулятора