Глава 2 переменное электромагнитное поле в однородной и изотропной проводящих средах

2.1. Уравнения Максвелла для проводящей среды

Рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью γ и магнитной проницаемостью μ_а.

Обратимся к первому и второму уравнениям Максвелла, записанным в комплексной форме для синусоидально изменяющихся во времени Е и Н:

В проводящей среде даже при весьма высоких частотах произведение ωε_а много меньше проводимости у. Поэтому с большой степенью точности слагаемым в первом уравнении Максвелла можно пренебречь.

В настоящее время наука не располагает точными данными о числовом значении относительной диэлектрической проницаемости е для металлов. Имеются лишь све­дения, что порядок е для металлов такой же, как и для большинства диэлектриков (т. е. от нескольких единиц до нескольких десятков). В качестве примера возьмем в для меди, равное 10, и найдем, во сколько раз ток проводимости в ней будет больше тока смещения при ω = 10³ и при ω = 10⁸ рад/сек. При ω = 10³

при ω = 10⁶

т. е. в рассмотренном числовом примере даже при ω = 10⁸ ток проводимости больше тока смещения в 6,33 10⁹ раз.

Таким образом, первое и второе уравнения Максвелла для прово­дящей среды приобретают вид

(2.1)

и

(2.2)

Эти два уравнения представляют собой уравнения с двумя неизвестными Е и Н. Проведем их совместное решение. С этой целью возьмем ротор от уравнения (2.1):

Учтем, что , и поэтомуgrad div = 0. Вместоrotв соответствии с (17.2) подставим -. Получим

(2.3)

Уравнение (2.3) является дифференциальным относительно В самом общем случае, когдазависит от всех трех или даже только от двух координат, решение (2.3) довольно сложно. Поэтому ограничимся рассмотрением решения уравнения (2.3) для частных случаев - для плоской и для цилиндрической электромагнитныхеолн,

2.2. Плоская электромагнитная волна

Под плоской электромагнитной волной понимают такую волну, для которой характерно, что во всех точках плоскости (например, плоскости хоу), перпендикулярной направлению распространения волны (оси z), напряженность электрического поля в данный момент времени одинакова (по величине и направлению) и лежит в плоскости хоу, точно так же и напряженность магнитного поля во всех точках плоскости хоу одинакова и лежит в плоскости хоу (рис. 2.1 иллюстрирует определение). На рис. 2.1 изображены для одного и того же момента времени векторы и в двух параллельных плоскостях, перпендикулярных осиz декартовой системы координат. Во всех точках первой плоскости (рис. 2.1а) напряженность электрического (магнитного) поля одинакова по величине и по направлению. Вовсех точках второй плоскости (рис. 2.1б) напряженность электрического (магнитного) поля также одинакова по величине и по направлению, но она не равна напряженности поля в первой плоскости.

В силу самого определения плоской волны

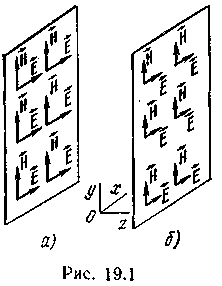
Рисунок 2.1

В плоской волне и являются функциями только одной координаты, в нашем случае функцией толькоz.

Повернем координатные оси таким образом, чтобы ось у совпала с напряженностью магнитного поля . При этом

где - единичный орт осиу декартовой системы координат. Подставим в уравнение (2.3) и раскроем :

(2.4)

Учтем, что

и

Получим

(2.5)

В уравнении (2.5) вместо частной производной написана простая производная. Переход от частной производной к простой для плоской волны вполне естествен, так как H является функцией только одной переменной z.

Уравнение (2.5) представляет собой линейное дифференциальное уравнение второго порядка. Его решение записывают следующим образом:

(2.6)

где С_х и С₂ - постоянные интегрирования; это комплексы, которые определяют из граничных условий; для каждой конкретной задачи свои постоянные.

Из характеристического уравнения найдем коэффициент

(2.7)

Если γ берется в единицах (ом м)^-1, μ_а в гн/м, то р измеряется в м^-1.

Так как , тор можно представить как:

(2.8)

где

(2.9)

Напряженность электрического поля найдем с помощью уравнений (2.1) и (2.6). Из (2.1) следует, что

Найдем rot. Имеем

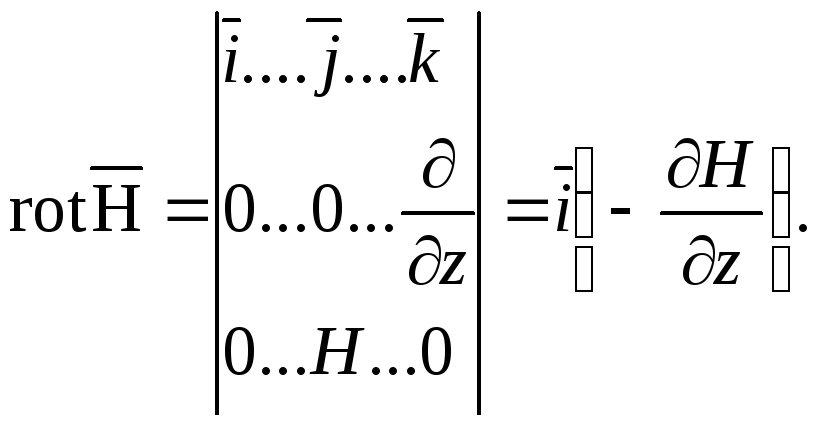(2.10)

Следовательно

(2.10^/)

Производная

(2.11)

Выражение (2.10') показывает, что напряженность электрического поля в плоской волне при выбранном расположении осей координат направлена вдоль оси х, об этом свидетельствует присутствие единичного орта оси x (орта ). Таким образом, в плоской электромагнитной волне между и есть пространственный сдвиг в 90° ( направлено по оси х, а - по осиу).

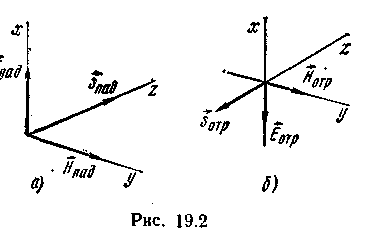
Рисунок 2.2

Частное от деления р на γ принято называть волновым сопротивлением:

Волновое сопротивление Z_B, измеряемое в омах, зависит от свойств среды (от γ и μ_а) и угловой частоты ω. В соответствии с (2.10') и (2.11) проекция на

ось х равна

где

и

Проекция на осьy:

и

Составляющие падающей волны _пад и _пад дают вектор Пойнтинга S_naд (рис. 2.2а). Он направлен вдоль положительного направления оси z. Следовательно, движение энергии с падающей волной происходит вдоль положительного направления оси z.

Составляющие отраженной волны _отр и _отр дают вектор Пойнтинга _отр(рис. 2.2б). Последний направлен вдоль отрицательного направления оси z. Это означает, что отраженная волна несет с собой энергию вдоль отрицательного направления оси z.

Волновое сопротивление Z_B можно трактовать как отношение Е_пад/Н_пад.

Так как волновое сопротивление является числом комплексным [см. (2.12)] и имеет аргумент 45°, то сдвиг во времени между Е_пад и Н_пад для одной и той же точки поля равен 45°.