Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

KONTROL_NAYa_RABOTA_PO_SOPROMATU_PGS_112152-18

.pdf

Скачиваний:

Добавлен:

31.05.2015

Размер:

1.31 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

9. Вычислим центробежные моменты инерции каждой части сечения относительно их собственных центральных осей

1) Уголок (знак минус принят, т.к. ось V с минимальным моментом инерции уголка проходит через отрицательные квадранты его собственной системы координат)

Dx1y1 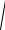Ix3 IV I y3 IV 27,10 16,3 90,9 16,3 28,4см4 .

2) Двутавр. Так как оси X2 и Y2 являются осями симметрии, то они главные для двутавра. Поэтому собственный центробежный момент инерции двутавра равен нулю по определению

Dx2 y 2 0 .

3) Лист. Так как сечение прямоугольное и оси X3 и Y3 являются осями симметрии, то они главные для сечения листа. Поэтому собственный центробежный момент инерции сечения листа равен нулю по определению

Dx3 y3 0 .

10. Вычислим осевые и центробежный моменты инерции сечения относительно центральных осей Xc и Yc

I Xc I Xi Ai yCi2 27,10 11,18 24,562 15380 61,9 5, 22

i 1

7,3 44,8 13,32 31757 см4 ;

IYc IYi Ai xCi2 90,9 11,18 11, 242 516 61,9 6, 462

i 1

3823 44,8 10,352 12480см4 ;

	3				28, 4 11,18 11, 24 24,56
D		D	A x y	ci	28, 4 11,18 11, 24 24,56
xcyc		xiyi	i ci	ci

i 1

0 61,9 6, 46 5, 2 0 44,8 10,35 13,3 10979см4.

11. Вычислим значения главных центральных моментов инерции всего сечения

				I Xc IYc		1								31757 12480
I				I Xc IYc		1	I	Xc	I	Yc	2 4 D2			31757 12480
I							I		I		2 4 D2
U V			2		2							XcYc	2
			2		2								2
	1
	1		31757 12480 2					4 109792				22118 14609 см4.
	2		31757 12480 2					4 109792				22118 14609 см4.
	2
I		22118 14609 36727см 4 ;										I 22118 14609 7509см 4.
U												V

12. Определим положение главных центральных осей инерции всего сечения

	2	2Dxcyc	2 10979	1,139;	24,36	0	24	0
tg								6 .
		Ixc I yc	31757 12480

13. Покажем главные центральные оси инерции на сечении. Ось V откладываем от оси Y, так как IYc IXc , на угол 240 6 , так, чтобы она проходила через положительные квадранты, так как Dxcyc 0 .

Сопротивление материалов

Сидоров С.С.

гр. 112???

Зд. № 3

Стр.10

								32
Y
	Y2	YC			Y3
45	72,5	160				160
							X3
			V		C3		7
			V		C3
			0
			25 06
180
		C			XC
	C2
		X2			U
		X2
180						288
	Y1
		13,6
C	1		42,4		X1
	1

0							X
59,6	30,4			Размеры указаны в миллиметрах
				Размеры указаны в миллиметрах
	172
Сопротивление материалов		Сидоров С.С.				гр. 112???	Зд. № 3	Стр.11

							33
Задача №4. Расчет деревянной балки круглого сечения на прочность (схема 0, строка 0)
K			q=14 кН/м		MB=146 кНм
K			q=14 кН/м
A						XB=0
F=22 кН	C			B
F=22 кН
	M=28 кНм
a=2 м		b=3,2 м	c=1,6 м		YB=73,2 кН
	Qy, кН					R=13 МПа
22						Rs=2 МПа
+
z0=1,57 м	6,0		–
z0=1,57 м			–
	0,43 м
					73,2
					146
	Mx, кНм
				-
16,0
	+
17,27
	44,08
			31 см
Сопротивление материалов		Сидоров С.С.		гр. 112???		Зд. № 4	Стр.12

1. Определим реакции опор

Y F q a b c YB 0;

Y q a b c

F 14 2 3,2 1,6 22 73,2кН.

M B F a b c

q a b c 2

M M B 0;

F a b c

q a b c 2

M 22 2 3, 2 1,6

14 2 3, 2 1,6 2

28 146кНм.

2. Построим эпюры поперечных сил и изгибающих моментов способом харак-

терных сечений.

В точка A (справа)

q=14

MA=0

F=22

QA=22

F=22

Qсправа 22кН;

Mсправа 0.

В точке K изгибающий момент вычисляем по площадям

z 22 1,57м;

0 1

22 1,57 17,27 кНм.

В точке С (слева)

q=14

-28

q=14

-14 2 1

F=22

22 2

a=2 м

Qслева 22 14 2 6кН;

M слева 22 2 14 2 1 16кНм.

В точке С (справа)

14 4,8

q=14

MB=146

-14 4,8 2,4

-146

q=14

MB=146

-73,2

YB=73,2

73,2 4,8

YB=73,2

b+c=4,8 м

Сопротивление материалов

Сидоров С.С.

гр. 112???

Зд. № 4

Стр.13

Qсправа	14 4б8 73б2 6кН;			M справа 146 73, 2 4,8 14			4,82	44,08кНм.
Qсправа	14 4б8 73б2 6кН;			M справа 146 73, 2 4,8 14				44,08кНм.
C				C	2
					2
В точке B (слева)
		q=14	MB=146		-146	q=14
			MB=146		-146			MB=146
								MB=146


	-73,2
		s 0	YB=73,2			s 0		YB=73,2
			YB=73,2

Qслева 73,2кН;			M слева 146кНм.
B			B

3. По условию прочности подберем деревянную балку круглого поперечного сечения, соблюдая условия: d 32см; R 13МПа; RS 2МПа.

Осевой момент сопротивления круглого сечения балки равен

W	I	X	d 4	d	d 3
					.

X	ymax		64	2	32

Из условия прочности по нормальным напряжениям определим требуемый диаметр сечения балки

M X

32M X

R .

d 3

n d 3

n 32

При n 1 (n –это принятое количество балок)

32 146 103

d 3

32M X

48,6см 32см.

n R

1 3,14 13 106

При n 4

32 146 103

d 3

32M X

30,6см<32см.

n R

4 3,14 13 106

Принимаем четыре балки диаметром

d 31см.

4. Вычислим осевой момент сопротивления принятого сечения балки.

WX d 3 3,14 313 2923см. 32 32

5. Проверим на прочность по нормальным напряжениям

M X	146 103	12,5МПа 13МПа.
nW	4 2923 10 6	12,5МПа 13МПа.
nW	4 2923 10 6
x

Недогрузка составляет

13 12,5 100 3,8% 15% . 13

Сопротивление материалов

Сидоров С.С.

гр. 112???

Зд. № 4

Стр.14

6.Проверим на прочность по касательным напряжениям (на скалывание) Статический момент отсеченной части

S 0		2		d	d 2		2		31		3,14 312	2339см3.

X	5		2		8	5		2		8

Осевой момент инерции сечения

J X d 4 3,14 314 45310см4. 64 64

Проверим по условию прочности

Q S 0			73,2 103 2339 10 6
Y		X		0,3МПа < R 2МПа.
				0,3МПа < R 2МПа.
nJ		d	4 45310 10 8 31 10 2	S
nJ	X	d	4 45310 10 8 31 10 2
	X

Условие прочности выполняется.

Сопротивление материалов

Сидоров С.С.

гр. 112???

Зд. № 4

Стр.15

							37
Задача №5. Расчет деревянной балки прямоугольного сечения
	на прочность (схема 0, строка 0)
XA=0		q=14 кН/м		M=28 кНм
XA=0		q=14 кН/м
A	C	K	D		B
	F=22 кН
YA=53,4 кН					YB=42,2 кН
a=2 м		2b=6,4 м		c=1,6 м
53,4	Qy, кН					R=13 МПа
53,4	47,4
	47,4
						Rs=2 МПа
+	25,4					h/b=2
				–
	z0=3,4 м	z1=3,0 м		42,2	42,22
	z0=3,4 м	z1=3,0 м
		Mx, кНм
		+		67,5
78,8
				95,5
		159,4
				16 см
Сопротивление материалов		Сидоров С.С.		гр. 112???		Зд. № 5	Стр.16

1. Определим реакции опор

M A

a 2b 2

M Fa YB a 2b c 0;

M A

14 2 6, 4 2

28 22 2 YB 2 6, 4 1,6 0;

YB 42,19кН 42, 2кН.

M B

a 2b

a 2b c q a 2b

c F

2b c M 0;

M B

2 6, 4 1,6 14 2 6, 4

2 6, 4

1,6

22 6, 4 1,6 28 0;

YA 53,41кН 53,4кН.

2.Построим эпюры поперечных сил и изгибающих моментов способом характерных сечений. Выполнить с подробными пояснениями как в п. 2 задачи 4 (см. выше).

3.По условию прочности подберем деревянную балку прямоугольного поперечного сечения, соблюдая условия: h 2b; R 13МПа; RS 2МПа.

Осевой момент сопротивления прямоугольного сечения балки равен

W	I X		bh3		h	bh2	.
X	ymax	12		2 6
	ymax	12		2 6

Из условия прочности по нормальным напряжениям определим требуемую ширину сечения балки

M X	M X		3M X	R .
nW	n	bh2	2b3n

X		6

При n 1 (n –это принятое количество балок)

b 3	3M X	3	3 159, 4 103	0, 264м=26,4см.
	2R n		2 13 106 1

h 2b 2 26,4 52,8см>32см. (не допускается).

При n 5

b 3	3M X	3	3 159, 4 103	0,154м=15,4см.

	2R n		2 13 106 5
h 2b 2 15,4 30,8см<32см. (допускается)
Принимаем пять балок с размерами			b 16см, h=32см.

Сопротивление материалов

Сидоров С.С.

гр. 112???

Зд. № 5

Стр.17

4. Вычислим осевой момент сопротивления принятого сечения балки

	bh2	16 322
W			2731см3.

X	6	6

5. Проверим на прочность по нормальным напряжениям

M X	159,4 103	11,67 МПа 13МПа.
nW	5 2731 10 6	11,67 МПа 13МПа.
nW	5 2731 10 6
x

Недогрузка составляет

13 11,67 100 10, 2% 15% . 13

6.Проверим на прочность по касательным напряжениям (на скалывание) Статический момент отсеченной части

	bh	h	b h2	16 322
S 0					2048см3.

X	2	4	8	8

Осевой момент инерции сечения

I X bh3 16 324 43691см4. 12 12

Проверим по условию прочности

Q S 0			53,4 103 2048 10 6
Y		X		0,31МПа<R 2МПа.
				0,31МПа<R 2МПа.
nI		b	5 43691 10 8 16 10 2	S
nI	X	b	5 43691 10 8 16 10 2
	X

Условие прочности выполняется.

32 см

16 см

Сопротивление материалов

Сидоров С.С.

гр. 112???

Зд. № 5

Стр.18

Задача №6. Расчет двутавровой балки с консолью на прочность и жесткость (схема 0, строка 0)

M=28 кНм

XA=0

F=22 кН

q=14 кН/м

23 мм

A C

26 мм

YA=52,1кН

YB=81,9 кН

2b=6,4 м

c=1,6 м

a=2 м

52,1	52,1	Qy, кН
	30,1	z1=4,25 м
	30,1		22,4
	+		22,4
	+
			+
		–
	z0=2,15 м
			59,5
		Mx, кНм
		17,9	–
			–
			10,1

E=200 ГПа R=210 МПа Rs=130 МПа V/L=1/500

104,2

136,56

Сопротивление материалов

Сидоров С.С.

гр. 112???

Зд. № 6

Стр.18

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.12.2018239.1 Кб15Kontrolnaya_09.doc
#
05.12.20182.39 Mб12Kontrolnaya_po_matem.doc
#
24.04.2019137.73 Кб13Kontrolnaya_rabota(1).doc
#
31.05.2015476.13 Кб80Kontrolnaya_rabota_gidravlika_metodichka_ok2.docx
#
26.03.2016137.73 Кб12Kontrolnaya_upravlenie_personalom.doc
#
31.05.20151.31 Mб9KONTROL_NAYa_RABOTA_PO_SOPROMATU_PGS_112152-18.pdf
#
31.05.20151.08 Mб109Kopia_Novaya_metod_izm_2014.doc
#
31.05.20151.4 Mб191Kopyr_Anufr.docx
#
26.03.2016713.73 Кб22KostikovaText.doc
#
15.07.2019930.75 Кб8Koлодзин. Как жить после психической травмы.rtf
#
31.05.2015134.21 Кб16KR2 информатика.pdf