Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1-2008

.pdf

Скачиваний:

Добавлен:

31.05.2015

Размер:

839.85 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Пример 12. Даны: функция

и вектор a . Найти: 1) grad z в т. точке A по направлению вектора a

z(x;

A ;

y) , точка

A(x0, y0

2) производную

)

z x2 xy y2;
	A(1;1);			a 2i	j.
Решение. 1) Градиент функции			z	имеет вид
grad z	дz	i	дx	j .
	дx		дy

Вычисляем частные производные в точке

Таким образом,

z'	x	2x y;
	x
z'	y	x 2 y;
	y

grad z 3i

z'	x		A	3;

z'		y	A		3.

3 j.

2) Производная

по

направлению

вектора

определяется по формуле

дz

cos

дz

sin ,

да

дx

ду

где

- угол, образованный вектором

с осью

OX . Тогда

cos

4 1

sin	ay	ay		1	1			.

	a	2	2	4 1		5

		ax	ay
Используя значения производных в точке							A

ранее, получим

, найденные

дz	3	2		3	1	3	.
дa
		5			5	5

			41

Перед решением задач 161-180 необходимо изучить пункты 12, 13, 14 программы.

Пример 13. Вычислить объем тела, ограниченного поверхностями

z 1;	z 2 x	2	;	y x	2	;	y 1 2x	2	.

Решение. Если область определена неравенствами

то объем

x b,

тела

y	(x) y y	2	(x),	z	(x, y) z z	2	(x, y),
1		2		1		2

находится по формуле

b		y2	(x)		z2	(x, y)
V	dx			dy		dz.
a		y	(x)		z	(x, y)
		1			1

Для определения пределов интегрирования сделаем чертеж данного тела и его проекции на плоскость XOY (рис 2а и 2б).

Следует обратить внимание на то, что для переменной x границами являются наибольшее и наименьшее значения в

заданной области, т.е.	1	x	1
				.
	3
			3

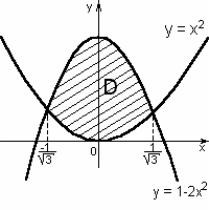
Рис. 2а

Переменная y является функцией переменной рисунке видно, что область D ограничена снизу кривой

а сверху – кривой y 1 2x2 . Следовательно,

x2 y 1

Рис.2б

x. На y x2 ,

2x	2	.

Аналогично, из рисунка

ограничено плоскостью

тела

,а

видно, что оно снизу сверху поверхностью

z 2 x2 . Таким образом, двух переменных x и y, и

переменная z является функцией

1 z 2 x	2

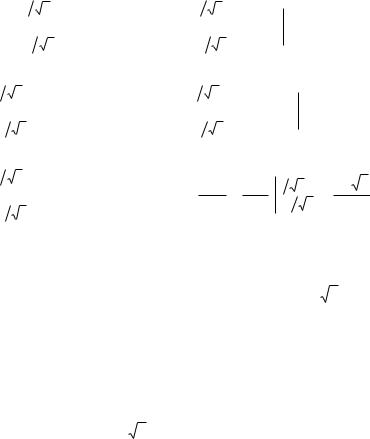
	1		3			1 2x			2			2 x		2			1	3			1 2x						2					2
	1		3			1 2x						2 x					1	3			1 2x								2	x		2
V				dx					dy						dz					dx						z			2	x			dy
V				dx					dy						dz					dx						z		1					dy
	1							2					1			1								2				1
			3				x	2											3			x		2
			3				x												3			x
1	3		1 2x				2									1		3																2
1	3		1 2x							2						1		3						2							1 2x			2
		dx					(1 x			2		)dy								(1 x				2		)( y)					1 2x			dx
		dx					(1 x					)dy								(1 x						)( y)					x	2		dx
					2																											2
1	3			x												1			3


1	3					2					2						4x		3		3x		5				1				3			56 3
		(1 x				2	)(1 3x				2		)dx (x				4x				3x				)		1				3			56 3	.
		(1 x					)(1 3x						)dx (x					3				5			)		1				3			135	.
1	3																	3				5					1				3			135
1	3
Пример							14.		Вычислить								объем					тела,									ограниченного

поверхностями

z 0;	z 1 x	2	y	2	;	y x;	y x	3

и расположенного в первом октанте Решение. Данное тело ограничено сверху параболоидом

1 x	2

y	2

. Область интегрирования

- круговой сектор,

ограниченный дугой линией пересечения

прямыми	y x	и	y
			V

окружностью				x	2	y	2	1	,	являющейся

параболоида				с	плоскостью						z 0 , и
x 3 . Следовательно,
(1 x	2	y	2	)dxdy .

	D
Поскольку	областью	интегрирования	является			часть
круга, а подынтегральная		функция зависит от		x	2	y	2	,
круга, а подынтегральная		функция зависит от		x		y		,
целесообразно	перейти	к полярным	координатам.

Преобразование двойного интеграла от прямоугольных координат x , y к полярным координатам , , связанным с

прямоугольными координатами соотношениями

cos

y sin , осуществляется по формуле

	f (x, y)dxdy	f ( cos , sin ) d d
D	D

Уравнение окружности

x	2	y	2	1

в этих координатах

примет вид

1, подынтегральная функция

пределы	интегрирования по						определяем
прямых:	tg	1, т.е.	1		;	tg	2	3 , т.е.
	1		1	4			2
				4

образом, имеем

равна	1	2	, а

из уравнений

2 3 . Таким

			2					3		1				2
V (1			2		) d d					d (				2	) d
V (1					) d d					d (					) d
D									4	0
3		1		2		1	4	1			1	3
		1		2		1	4	1	d		1		d				.
									d				d				.
	4	2				4		0			4		4			48

Перед решением задач 181-200 необходимо изучить пункты 15 программы.

		Пример	15. Вычислить				криволинейный интеграл
(x	2	y 3x)dx	( y	2	x 2 y)dy	вдоль	1) ломаной L ABC от

L

точки A(1;0) x 3cos t,

до точки

y 2sin t

C(2;5) , где B(2;3)	;
(0 t / 2).

2) дуги эллипса

Решение. Пусть параметрической форме

кривая

x (t),

L задана уравнениями y (t) . Пусть точкам M

P этой кривой соответствуют значения параметра t соответственно.

Тогда

(P)

(M )

X (x, y)dx Y (x, y)dy X (t), (t) (t) Y (t), (t) (t) dt.

Если кривая задана уравнением

M соответствует		x a , а точке P -		x
(P)		b	X x,
	X (x, y)dx Y (x, y)dy			f (

b , x)

f (x) , причем точке то

Y x, f (x) f (x) dx.

(M )

1) Криволинейный интеграл вдоль ломаной L можно разбить на сумму двух интегралов: вдоль отрезков AB и BC. Запишем уравнение прямой, проходящей через две точки A и B

AB :	x 1		y 0		;	y 3(x 1).
	2	1	3	0

Найдем производную y

Уравнение отрезка BC

имеет вид

dx 0,

3 y 5. Таким образом,

(C)

(B)

y 3x)dx ( y

x 2 y)dy

2	. В этом случае

3x)dx ( y	2	x 2 y)dy

( A)													( A)
(C)							2		(x 1)3 3x 9(x 1)						x 6(x 1) 3 dx
(y		2	x 2 y)dy x					2						2
(y			x 2 y)dy x
(B)							1
5				2			2			3		2				2		3		2		5
(2 y						2 y)dy 3 (10x					19x		14x 6)dx (			2	y		y		)

																3						3
3							1															3


8	1		81		2		89.5
8	6		81		6		89.5
	6				6

3) Кривая задана в параметрическом виде. Найдем производные

	3sin t;		2cos t .
xt		yt

Тогда

(x		2	y 3x)dx ( y										2	x 2 y)dy
(x			y 3x)dx ( y											x 2 y)dy
L

	2					2																	2
	(9 cos					2		t2 sin t				9 cos t)( 3sin t)							(4 sin				2		t3cos t 4 sin t)2 cos t) dt
	(9 cos							t2 sin t				9 cos t)( 3sin t)							(4 sin						t3cos t 4 sin t)2 cos t) dt
	0

	2			27		sin 2t(sin 2t 1) 4 sin 2t(												3		sin 2t
						sin 2t(sin 2t 1) 4 sin 2t(														sin 2t					1) dt
	0			2														2
	0

	2			15	sin				2		2t		35		sin 2t	dt	2				15	(1		cos 4t)		35	sin 2t
				15					2				35								15					35
																												dt
				2									2								4					2
	0			2									2				0				4					2
	0																0
		15					35			.
		8						2		.
		8						2

Приложение 1

Таблица производных простейших элементарных функций.

I. (С) = 0.

	1	1		1
II. (x ) x 1, в частности			, ( x )
					.
		x2
	х			2 x

III.	(logа х) =	1	logа е, в частности			(ln х) =
III.	(logа х) =	x	logа е, в частности			(ln х) =
		x
IV.	(a x ) a x ln a,			в частности,	(e x ) e x .
V. (sin х) = cos х.
VI.	(cos х) = sin х.

1 x

VII. ( tg x ) =

1		.
	2
cos		x

VIII. (ctg x) =	1			.
VIII. (ctg x) =		2		.
	sin	2		x
	sin			x
IX. (arcsin х) =				1
IX. (arcsin х) =					2
			1 x		2
			1 x

X.	(arccos x) =			1	.


			1 x2
			1 x2
XI.	(arctg x) =	1		.
XI.	(arctg x) =	1 x	2	.
			2

XII. (arcctg x) =					1
XII. (arcctg x) =					x
				1	x
XIII.	(sh х) = ch х.
XIV.	(ch х) = sh х.
XV. (th x) =		1			.
XV. (th x) =			2		.
		ch	2	x
		ch		x
XVI.	(cth x) =				1
XVI.	(cth x) =			sh2
				sh2

Приложение 2

Таблица интегралов простейших элементарных функций

					1
I.			dx		x
I.		x	dx		1
					1
II.		dx	ln x C.
		x


III.		dx		arctg
III.	1 x2			arctg
	1 x2

C 1 .

xC.

IV.

	dx	arcsin x C.

	1 x	2

a x
V. a xdx ln a C	0 a 1 .

VI.

VII.

VIII.

IX .

e x dx e x C.

sin x dx cos x C.

cos x dx sin x C.

	2
dx		tg x C.
		tg x C.
cos		x

X.

XI.

	dx			ctg x C.
		2		ctg x C.
sin		2	x
sin			x
		dx			1	ln	x a	C
	2	a		2	2a	ln	x a	C
x	2			2	2a		x a
x

XII.

	dx		ln x	x	2	k	C.
	2	k
x

XIII.

		dx		1	arctg	x	C.
x	2	a	2	a		a

XIV.

	dx			arcsin	x	C.
	2	x	2		a
a

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Пискунов Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов - М.: Наука, 1985. Т.1. 432 с. .

2.Данко П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова - М.: Высшая школа. 1986. Ч. 2.

3.Пискунов Н. С. Дифференциальное и интегральное

исчисления / Н.С. Пискунов - М.: Наука, 1978. Т.2. 575 с.

4.Бугров Я.С. Дифференциальные уравнения. Кратные интегралы. Функции комплексного переменного / Я.С.Бугров, С.М. Никольский – М.: Наука, 1985.

5.Кузнецов Л.А. Сборник заданий по высшей математике

/Л.А. Кузнецов - М.: Высшая школа. 1994. 172 с.

	СОДЕРЖАНИЕ
1.	Общие рекомендации студенту-заочнику к изучению
	курса высшей математики . . . . . . . . . .	. . . . . . . . . . . . . . .	1
2.	Программа курса “Высшая математика” для студентов-
	заочников инженерно-технических специальностей. . . .		3
3.	Правила выполнения и оформления контрольных работ		5
4.	Вопросы для самопроверки к контрольной работе №5. .		5
5.	Вопросы для самопроверки к контрольной работе №6. .		6
6.	Задачи для контрольных заданий. . . . .	. . . . . . . . . . . . . . .	7
7.	Примеры решения задач к контрольной работе №5 . . . .		23
8.	Примеры решения задач к контрольной работе №6 . . . .		36
	Приложение 1 . . . . . . . . . . . . . . . . . . . .	. . . . . . . . . . . . . . .	45
	Приложение 2 . . . . . . . . . . . . . . . . . . . .	. . . . . . . . . . . . . . .	46
	Библиографический список . . . . . . .	. . . . . . . . . . . . . . .	47
	50

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
26.03.2016682.05 Кб290_Homework.pdf
#
31.05.20152.8 Mб481 Глава.doc
#
31.05.20151.44 Mб661 курс ИСиТ методичка (2 семестр) .pdf
#
31.05.2015301.57 Кб301 курс логика заочники.doc
#
31.05.2015388.61 Кб371 МЕТОДА МиМАПР.doc
#
31.05.2015839.85 Кб71-2008.pdf
#
26.03.20161.53 Mб101-2009 ДГЦУиМП.pdf
#
31.05.201588.06 Кб311. Охрана труда.doc
#
31.05.2015329.22 Кб461. Постоянный ток.doc
#
31.05.201584.99 Кб71.doc
#
26.03.20162.1 Mб111.УМКД. Гидр.ТМ.ДО.doc