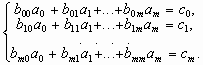Изучая в лабораторной работе № 3 теорию интерполяции, вы познакомились с интерполяционными формулами, которые в точности воспроизводят значения данной функции в узлах интерполяции. Однако в ряде случаев выполнение этого условия затруднительно или даже нецелесообразно:

1. Если заданные величины х и у являются экспериментальными данными, то могут содержать в себе существенные ошибки, т.к. получены в результате измерений или наблюдений. Поэтому построение аппроксимирующего многочлена, воспроизводящего в точности заданное значение функции, означало бы тщательное копирование допущенных при измерениях ошибок.

2. Если имеются точные значения функции в некоторых точках, но число таких точек n весьма велико, то интерполяционный многочлен будет очень высокой степени (если только разности не будут становиться постоянными).

Поэтому возникает задача построения многочлена некоторой вполне определенной степени, но меньшей чем n - 1, который хотя и не дает точных значений функции в узлах интерполяции, но достаточно близко к ним подходит.

 

Метод наименьших квадратов

 

Метод наименьших квадратов (МНК) состоит в следующем: для данных значений x = х₀, х₁, . . ., х_n и y = y₀, y₁, . . ., y_n подобрать многочлен заданной степени m<n вида

(1)

принимающий в заданных точках х_i значения как можно более близкие к табличным значениям y_i. Коэффициенты a_i многочлена (1) находят из решения системы

где .

(2)   (3)

 

Регрессионный анализ

 

Пусть имеются два ряда чисел x = х₀, х₁, . . ., х_n и y = y₀, y₁, . . ., y_n, при этом предполагается, что ряд у каким-либо образом зависит от ряда х. Задача регрессионного анализа состоит в восстановлении математической зависимости (регрессии) у(х) по результатам измерений (x_i, y_i), i = 0, 1, . . ., n.

Mathcad включает ряд функций для вычисления регрессии. Функции отличаются прежде всего типом кривой, которую они используют, чтобы аппроксимировать данные.

1. Математика в почвоведении

Во введении в основном говорилось об общих вещах: о современных экологических и эколого-экономических проблемах, о проблеме Нас и Мира. Мы выяснили, что необходимо изменить современную технократическую парадигму на гуманистическую экологическую (или, по крайней мере, на эколого-экономическую), то есть перейти от рассудка к разуму. Решить эти проблемы можно только с позиции системных и экосистемных принципов. Их применение, в свою очередь, требует другой методологии и других методов.

Материал курса довольно сложен, кроме того, нет специальных учебников по моделированию и системному анализу в почвоведении. Статьи и монографии по частным вопросам и учебники для математических специальностей очень трудны для не математиков. В результате актуальность создания такого учебника вполне очевидна.

Итак, начнем, как говорили древние римляне, ab ovo.

То есть с начала или в буквальном переводе с латыни «с яйца».

Развитие почвоведения как фундаментальной науки и практические потребности общества требуют разработки новых теорий и гипотез, углубления уже существующих: в этом заинтересовано прежде всего производство. Однако существенным препятствием на пути к этому подчас становятся имеющаяся в арсенале почвоведения методология и методы получения новых знаний.

По нашему мнению, рост знания – это процесс, чем-то похожий на дарвиновскую триаду процесса эволюции. Насколько вы помните из общих курсов биологии, – это наследственность, изменчивость, отбор. О чем это говорит? Разнообразие (изменчивость) складывающих науку гипотез, которые основаны на более ранних теориях (наследственность), является благом, поскольку позволяет нам отобрать из них наиболее соответствующие современному этапу развития знаний (отбор).

Арсенал методов почвоведения довольно обширен. Это, помимо сравнительно-географического метода, и методы химии, физики, гидрологии и многие другие. Правда, не все они равноценны и не всегда решают все возникающие в процессе почвенных исследований вопросы. Таких нерешенных вопросов накапливается в теории и практике почвоведения все больше и больше.

Что же в связи с этим можно сделать? Опираясь на опыт смежных с почвоведением наук (экологии, географии, картографии, теоретической биологии), можно предположить, что важную роль в преодолении этих узких мест теоретического и практического почвоведения должны игратьать математические методы.

1.1. Замечания по поводу применения математики в почвоведении и экологии

Давно уже стало общим правилом, почти поговоркой, что

Математика – это метод, что она, как мельница, с успехом перемалывает любое зерно, которое в нее засыпают, что математика применима практически во всех науках – как естественных, так и общественных.

Математика является мощным инструментом при изучении практически всех процессов и явлений, которые происходят в реальном мире. Сейчас это признали и почвоведы, и даже «классические» биологи, которые 30–40 лет назад считали, что математические методы механистичны и «чужды духу наук о природе». По поводу статей о природных объектах с применением (даже весьма скромным) математики тогда со злой иронией говорили, что «здесь природы нет – остались одни уравнения». Это происходило потому, что многие смотрели на уравнения, как неопытный конькобежец на коньки: и неловко, и опасно, в общем, без них много проще. Это издержки недостаточного математического образования. Стоит овладеть уравнениями, и вы сразу увидите за каждой их буквой и движение воды в почве, и потоки тепла в ней, и многое другое (Арманд, 1975). Кроме того, вы более ясно представите связи между протекающими в почве и экосистеме процессами. Увидите связи между почвой и экосистемой – то есть станете опытными конькобежцами, которым ничего больше не мешает.

Конечно же, природа не математика, хотя бы потому, что она материальна, а математика абстрактна. Гораздо ближе к изучению природы стоят физика и химия. Однако в основе всех физических и химических явлений и процессов лежат математические законы, такие же законы лежат в основе и музыкальной гармонии, и архитектуры, и «во многих других местах». Как бы сказал Давид Львович Арманд, математика – это пустой каркас, канва без вышивки, но когда природа начинает вышивать свои узоры, то они ложатся только по ячейкам этой канвы (Арманд, 1975). Поэтому-то и говорят, что математика – главный источник представлений и признаков, на основе которых и появляются новые теории, методологии и методы (Харвей, 1974; Ляпунов, Багриновская, 1975; Кноринг, Деч, 1989).

Не путать с Алексеем Давидовичем Армандом.

Особая ценность математики для построения теории, методологии и осмысления полученных практических данных состоит в том, что она помогает исключать в процессе мышления все лишнее, выделять главное, наиболее существенное (или наоборот, увидеть нечто, на первый взгляд не видимое, недоступное простому здравому смыслу). Математика имеет удивительную способность экономить мыслительную работу, не давая соскользнуть в пропасть фантазий, столь милых сердцу традиционного биолога, эколога и почвоведа. Образно говоря, методы математики – это прямая магистраль, идущая из пункта «А» (поставленного вопроса) в пункт «В» (полученного ответа). Конечно, в пункт «В» можно попасть и по проселочным дорогам эмпирического знания. Однако путь по этим разветвленным и запутанным дорогам не близок и может привести совсем в другое место.