64

М.Ф.Жоровков

В случае диаграмм состояния построенных на основе графиков (h-s)_P и (f-v)_Tнеобходимо знание коноды или же ее проекции на ось абcцисс и т.д.

Равновесие в системе жидкость газ

Мы рассмотрели схему, согласно которой, если задать свойства фаз, т.е. уравнение состояния , в виде определенных линий на соответствующих графиках, то можно графически исследовать поведение двухфазной равновесной системы. Применим это к исследованию равновесия жидкость газ. Эта проблема не однократно решалась на разных теоретических уровнях в статистической физике и продолжает решаться. Му рассмотрим упрощенную, но качественно удовлетворительную модель Ван-дер Ваальса. Особенность системы жидкость- газ заключается в том, что две фазы – жидкая и газообразная имея различную плотность на отличаются друг от друга макросимметрией. Для анализа равновесия в системе имеется простое аналитическое уравнение Ван-дер Ваальса. Для построения диаграммы воспользуемся методами геометрической термодинамики.

Уравнение Ван-дер- Ваальса можно записать как результат обобщения уравнения состояния идеального газа. Pv=RT для одного моля газа. В отличие от модели идеального газа в модели Ван-дер-Ваальса учтены: 1) собственные размеры атомов – посредством замены в уравнении объема системыvдоступным или свободным объемом (v-b), гдеb- суммарный собственный объем атомов или молекул;

2) Притяжение между молекулами в виде внутреннего, отрицательного давления –a/v², обратно пропорционального квадрату объема; В уравнении Ван-дер Ваальса вместо полного давленияP входит разностьPи(-a/v²)

Таким образом, собираем уравнение Ван-дер-Ваальса в виде (P+a/v²)(v-b)=RT илиP=RT/(v-b)-a/v².

Последняя запись в явном виде определяет изотерму Ван-дер-Ваальса [P(v)]_T.Качественный вид изотермы можно исследовать, получив ее экстремумы.

.

Следовательно, экстремумы соответствует решением кубического уравнения.

Это уравнение легче всего исследовать графически, как точки пересечения линии и прямойна вспомогательном графике. Линияy₁ характеризуется следующим: y₁(b)=0 (b – наименьшее, возможное значение объема). y₁()=0 приv=b, v= иv=3b так как.

Далее max y₁=y₁(3b)=4/(27b);Горизонтальy₂ при малых значениях температурыT (рис .26) пересекает кривую в двух точках, что соответствует двум экстремумам изотермы[P(v)]_T.При высоких температурах горизонтальT>T_кр.не пересекает кривуюy₁(v), что означает отсутствие экстремумов на изотерме[P(v)]_TКритическая температураT_кр, при которой исчезают экстремумы на изотерме определится из условияy₂=max y₁ как T_кр.=(8/27)(a/Rb), а критическое давление получается подстановкой в уравнение Ван-дер-Ваальса значенияT_кр.

P_кр.=(1/27)(a/b²).

ПосколькуT_криP_кр экспериментально определяемые величины, то их эмпирические значения могут быть использованы для оценки констант. Уравнение Ван-дер-Ваальса качественно весьма хорошо соответствует экспериментальным данным, а в некоторых случаях дает и количественные совпадения. На основе графика (y-v)можно воспроизвести качественный вид изотермы Ван-дер-Ваальса.

1. При T>T_кр. Изотермы не имеют экстремумов. Поскольку при неограниченном возрастанииv (уравнение Ван-дер-Ваальса переходит в уравнение состояния идеального газа)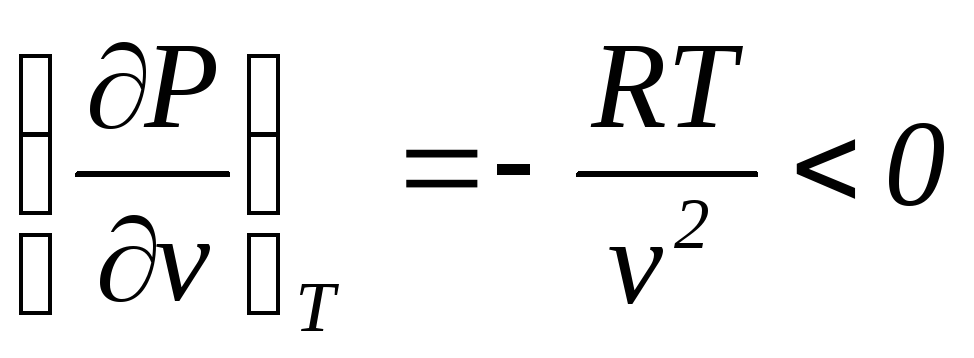; можно заключить, что приvпри_.Изотермы на всем протяжении имеют отрицательный наклон и тем самым удовлетворяют условиям механической устойчивости

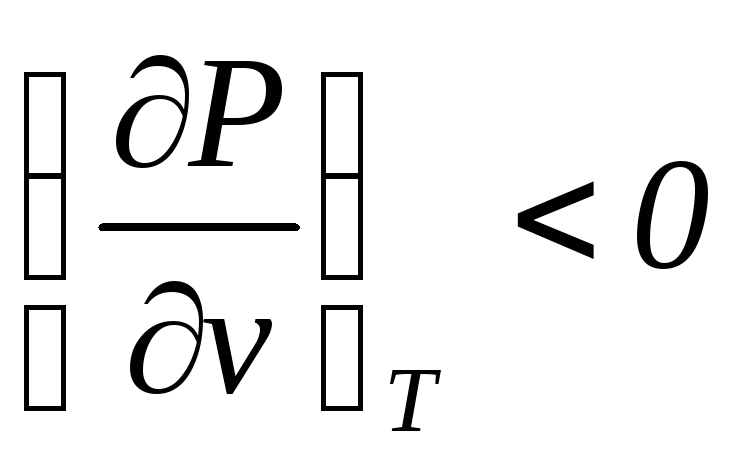
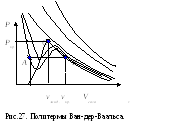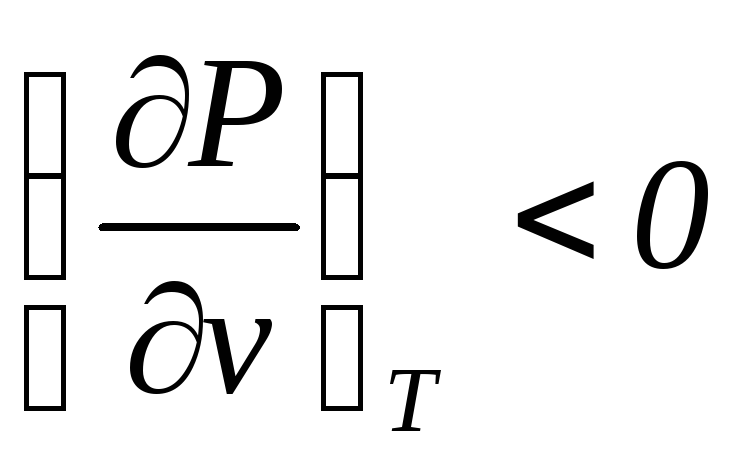2. ПриT<T_кризотермы содержат два экстремума. Поскольку и а этом случае для большихv, то правый экстремум являетсяmax, а левыйmin.С повышением температуры все изотермы смещаются вверх; При приближении кT_крэкстремумы сближаются и исчезают в определенной критической точке. ТочкаC на рис.27.