attachments_26-06-2014_11-15-27 / Лекц 12 Пар 10 Прям произв об ф

Для классических функций f x , x

n , и g y , y m , их

произведение

f x g y задаѐтся формулой f x g y (x, y) f x g y .

Если функции

f x и g y локально интегрируемы, то таково и их

произведение

f x g y . Для соответствующих регулярных обобщѐнных

функций верны равенства

f x g y , x, y

f x g y x, y dxdy

n m

f x g y x, y dydx f x , g y , x, y .

n

m

Положим эти равенства в основу общего определения.

Определение 10.1. Пусть

f D'

n ,

g D'

m − произвольные

f x g y , x, y f x , g y , x, y ,

(74)

где x, y D

n m .

Корректность этого определения вытекает из следующей теоремы

Теорема 10.2. Функция x g y , x, y является основной

функцией для любой функции x, y D

n m .

x

R n

Px

0

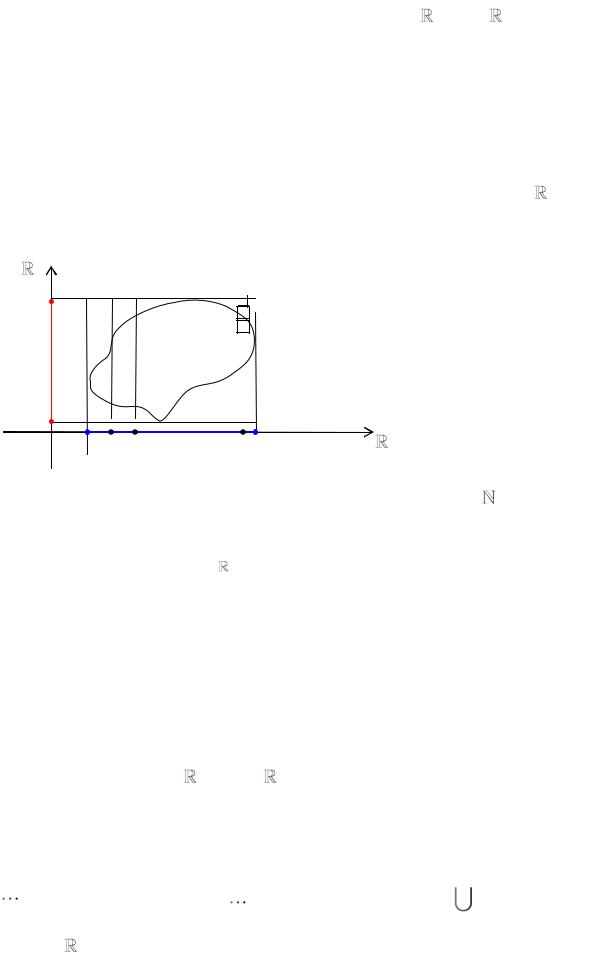
Обозначим через P ,

P проекции носителя supp x, y на n и на m

x

y

потому supp x Px . Следовательно, x − финитная функция.

Докажем теперь, что функция x непрерывна. Пусть x

x

в n .

n

Легко понять, что интерес представляет лишь случай x Px .

m

Ox

Py

supp x, y

K

K1 K2

x1

x

x

n

2

Px

Рассмотрим (очевидно, компактные) множества Kn xn Py , n , и

K x Py (см. рисунок выше).

Установим теперь, что xk , y

D( m )

x , y , т.е. что

( )

Справедливость п. 1) очевидна. Докажем 2). Пусть 0 . Функция y x, y

непрерывна, поэтому можно окружить каждую точку из K прямоугольной

окрестностью U V , где U

n и V m так, чтобы колебание (разность

U1 V1,

,Ul Vl . Пусть Ox

U1

Ul . Тогда

Ox

Py l

Ui Vi . Так

i 1

как x x в n , то существует номер N такой, что

x O

при n > N. Тогда

k

n x

принадлежит множеству

l

U

i

V , и поэтому

( ) x

, y ( ) x

, y

для

i

n

i 1

любого y . Значит мы доказали равномерную сходимость

( ) x

, y ( ) x , y на

x , y

D( m )

x

, y . Так как

P . Следовательно,

k

y

k

существование частной производной

. Существование других частных

x

1

производных первого и высших порядков доказывается аналогично.

Рассмотрим вектор e 1,0,

,0

в

n и произвольное h

1,1 . Нам нужно

1

установить существование предела lim

1

x h e1 x .

h 0 h

Для этого определим функцию h

x, y

1

x h e1, y x, y .

h

при каждом x

n h x, y

x, y при h 0 . Докажем сходимость

x1

D n

h x, y

x, y .

(*)

h 0

x1

1) носитель supp h x, y является компактом. Множество

supp x h e1, y – это сдвиг компакта supp x, y «вдоль» вектора e1 на h. Так

h

, то все множества supp

1

как

1,1

x h e , y

будут лежать в одном

компакте K0 . Поэтому все носители supp h x, y будут лежать в одном

компакте K K0 supp x, y .

2) Зафиксируем x

n произвольно. Тогда, рассуждая аналогично

доказательству непрерывности функции

x (но опираясь на

( )

x, y по x1) , нетрудно убедиться, что

дифференцируемость y

( ) x, y

1

( ) x h e , y ( ) x, y

( ) равномерно по y на

h

y

y

1

y

h

x1 y

( )

( )

x, y

− непрерывные функции.

компакте K, так как y x h e1, y и

y

Теперь, используя непрерывность обобщѐнной функции g D'

m ,

можем заключить:

lim

1

x h e1 x lim

1

g( y), x h e1, y g( y), x, y

h 0 h

h 0 h

lim g( y), h x, y g( y),

x, y

для произвольного x

n .

h 0

x1

Мы доказали, что функция x дифференцируема по переменной x1,

причѐм

(x) g( y),

x, y .

■

x1

x1

Теорема 10.3. Соответствие (x) T (x) g y , x, y − есть

линейное и непрерывное отображение T : D

n m D

n .

Линейность этого преобразования очевидна. Докажем его непрерывность.

Достаточно показать, что из сходимости k 0

в D

n m следует

сходимость T k k 0 в D

n

при k . Так как k 0 , то:

1)

Существует компакт K , содержащий носители всех функций k x, y ,

2)

( )

( )

x, y 0 на K при любых мультииндексах и .

k y

x

Обозначим Kx − проекцию компакта K на первый сомножитель в

произведении

n

m . Тогда

3)

supp k x supp g y , k x, y Kx

для любого k, и

( )

x

( )

g y ,

( )

x, y

Kx

4) k

g y , k x, y x

k x

0 . ■

k