6. Вычисление площади плоской фигуры

I. Вычисление площади плоской фигуры в декартовых координатах

1) Площадь криволинейной трапеции

Определение 1. Криволинейной трапецией называется фигура, ограниченная графиком функции y=f(x), где fC[a;b], a<b, f(x)≥0, x[a;b], прямыми x=a и x=b и отрезком [a;b] оси Ox.

Теорема 9. Криволинейная трапеция представляет собой квадрируемую фигуру F, площадь которой

. (13)

Доказательство.

1) Криволинейная трапеция F ограничена тремя отрезками и графиком непрерывной функции f. Тогда по теореме 5 F – квадрируема.

2) Найдём(F).

Возьмём отрезка [a;b] на частичные отрезки ,. Обозначим черезинаименьшее и наибольшее значения функции на. Составим суммыи. Очевидно,и- площади описанного и вписанного околоF многоугольников. Следовательно,

. (14)

По условию fC[a;b] .

Переходя к пределу в (14), получим (13).

Геометрический смысл определенного интеграла.

Определенный интеграл равен площади криволинейной трапеции, ограниченной графиком функции y=f(x), где fC[a;b], a<b, f(x)≥0, x[a;b], прямыми x=a и x=b и отрезком [a;b] оси Ox.

2) Фигура F ограничена графиком функции y=f(x), где fC[a;b], a<b, f(x)≤0, x[a;b], прямыми x=a и x=b и отрезком [a;b] оси Ox.

тоже будем называть криволинейной трапецией. Т. к. f(x)≤0, то -f(x)≥0, и, значит, к фигуре F₁ можем применить формулу 1:

.

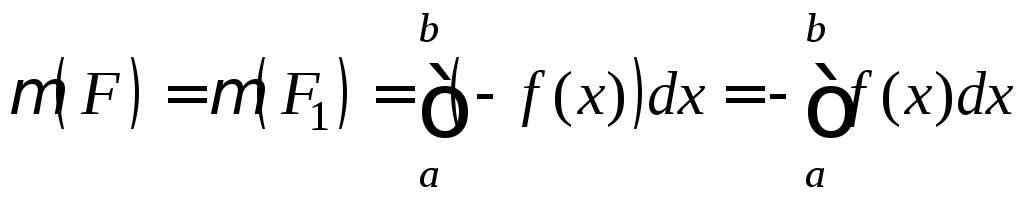. (15)

3) иf(x) меняет знак в конечном числе точек [a;b].

Разобьем фигуру F на части, в каждой из которых f(x) не меняет знак, и применим ответствующую формулу (13) или (15).

,

.

4) Фигура ограничена снизу графиком функцииy=f₁(x), сверху - y=f₂(x), ,, и с боков прямымиx=a, x=b.

F=F₂\F₁, где F₁ ограничена сверху графиком y=f₁(x), а F₂ – графиком y=f₂(x). Так как , то

.

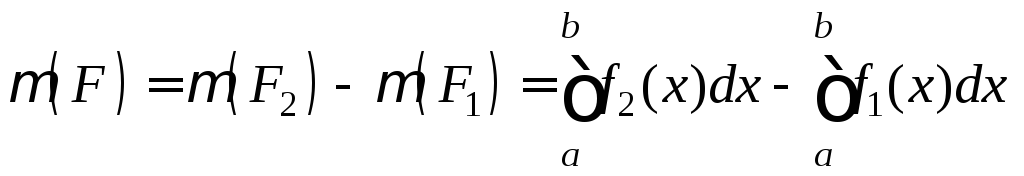По свойству интеграла .

II. Площадь криволинейной трапеции, ограниченной кривой, заданной параметрическими уравнениями

Теорема 10. Пусть криволинейная трапеция ограничена кривойАВ, заданной параметрическими уравнениями: .

Если: 1)и,

2) и,

3) ,

то криволинейная трапеция квадрируема и справедлива формула:

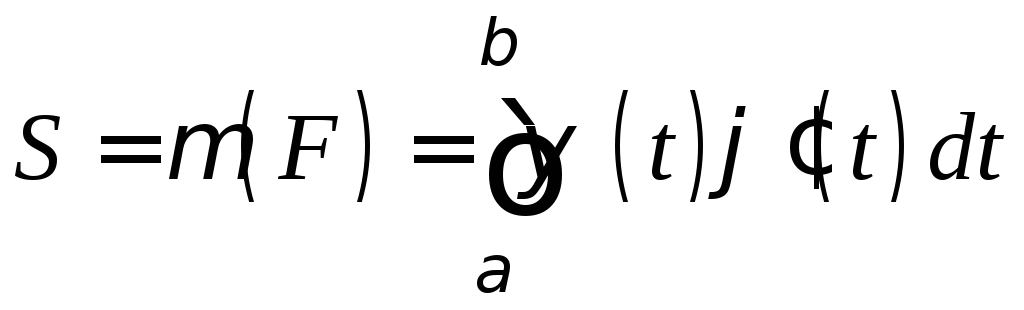. (16)

Доказательство.

Так как , то существует обратная функция, возрастающая и непрерывная на [a;b]. Следовательно, .Таким образом, криваяАВ является графиком функции y=f(x), где . Тогда по теореме 9 криволинейная трапеция квадрируема и её площадь

.

Выполним здесь подстановку: .

. Т. о., получаем (16).

Формула (16) справедлива и для случая .

Если (0tT) – параметрические уравнения простой замкнутой кривой, пробегаемой против хода часовой стрелки и ограничивающей слева от себя фигуру F, то площадь фигуры можно вычислить по одной из формул:

, ,

. (17)

Пример.Вычислить площадь фигуры, ограниченной астроидой .

 Т. к. фигура F ограничена замкнутой линией, то удобно применить формулу (17).

. 

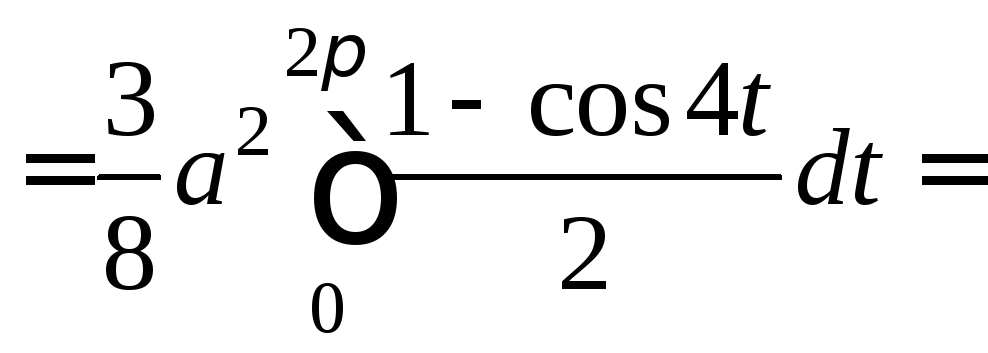
III. Площадь в полярных координатах

1) Пусть кривая L задана в полярной системе координат уравнением:

.

Определение. Криволинейным сектором называется плоская фигура, ограниченная кривой L и двумя лучами, составляющими с полярной осью углы .

Теорема 11. Криволинейный сектор представляет собой квадрируемую фигуру F, площадь которой вычисляется по формуле:

.

Доказательство.

Выберем произвольное разбиение отрезка точкаминаn частей . Проведём лучи. Сектор разбит наn частей. Т.к. , то на каждом из частичных отрезковона имеет наибольшееи наименьшеезначения. Напостроим два круговых сектора с радиусамии. Получим две ступенчатые квадрируемые фигуры. Одна из нихP содержится в секторе, а другая Q его содержит. Площади этих ступенчатых фигур

, , .

и - нижние и верхние интегральные суммы для функции, то есть, .

Так как функция , то она интегрируема на, то естьвыполнено. Пусть<. Тогда по теореме 2 фигура F квадрируема (так как нашлись две квадрируемые фигурыP и Q, , такие, что).

Так как функция интегрируема на, то

.

Так как , то.

2) Пусть фигура ограничена кривыми ,, на и лучами=, =. Тогда

.
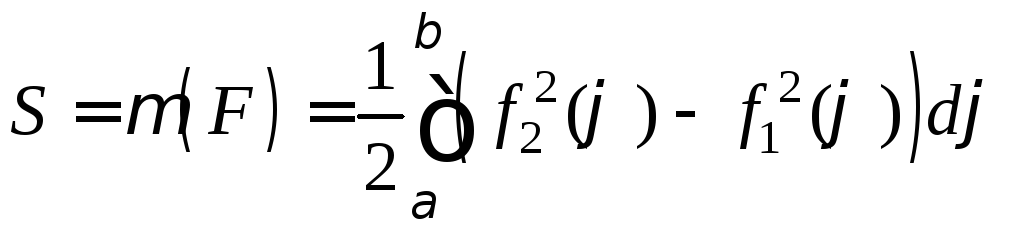