Арифметические операции во множестве рациональных чисел

Определим во множестве Q операции сложения, умножения, и их свойства.

1. Сравнение. Пусть даны два рациональных числа K() и K().

Определение: Два рациональных числа называются равными, если они представлены эквивалентными дробями.

Другими словами K() = K() ad = bc

Определение: Суммой двух рациональных чисел K() и K() называется рациональное число K().

Таким образом, K() + K() = K()

Теорема: Сумма двух рациональных чисел K() и K() не зависят от выбора их представителей.

Доказательство:

Пусть даны два рациональных числа K() и K(), их сумма определяется рациональным числом K() . Пусть K() и K(), их сумма по определению определяется K(). Покажем, что K() + K() = K() + K(), а для этого нужно показать, что ~.

Доказательство:

Так какK() ~ a'b = b'a Умножим обе части равенства на dd'.

Так как K() ~ c'd = d'c Умножим обе части равенства на bb'.

a'bdd' = b'add'

+

c'dbb' = d'cbb'

a'bdd' + c'dbb' = b'add' + d'cbb'

bd(a'd+ b'c') = b'd'(ad + bc)

Это равенство означает, что ~ , то есть

K().

Определение: Произведением двух рациональных чисел K()и K() называется рациональное число K().

Таким образом, K() * K() = K().

Теорема: Произведение двух рациональных чисел K() и K() не зависит от выбора их представителей.

Дано: K(); K() – рациональные числа, K() * K() = K().

ПустьK() и K(), тогда K() * K() = K().

Доказать: K() = K(), то есть ~.

Доказательство:

Так как K(), то ~  a'b = b'a

так как K(), то ~  c'd = d'c

Перемножим почленно эти равенства: a'bc'd=b'ad'c или (ac)(b'd')=(bd)(a'c'). Это равенство означает, что ~, то есть K().

Определение: Разностью двух рациональных чисел K() и K() называется рациональное число K(), которое удовлетворяет равенству:

K() + K() = K().

Теорема: Разность любых двух рациональных чисел существует и единственна.

Доказательство:

I. Существование.

а) Найдем вид числа K(). По определению разности оно удовлетворяет условию:

K() + K() = K().

По определению суммы K() + K() = K()  K() = K( ).

Но два рациональных числа равны, если ~, то есть если

ady = b(cy + dx). Тогда, ady = bcy + bdx  ady - bcy = bdx y(ad – bc) = bdx 

~  K() = K( ).

б) Покажем, что найденное рациональное число является разностью чисел K() и K(). Проверим выполнимость равенства: K() + K() = K().

K() + K() = K() = K() = K() = K(), так как~ .

Итак, существование разности доказано. Докажем ее единственность.

II. Единственность разности.

Предположим, что существует две разности рациональных чисел K() и K(), то есть K() – K() = K() и (1) K() – K() = K() (2)

Покажем, что K() = K(). Из (1) следует, что K() = K() + K(); из (2) следует, что K() = K() + K(). Тогда K() + K() = K() + K().

По определению суммы имеем: K() = K(), что возможно, если ~.Тогда по определению равносильных дробей имеем:

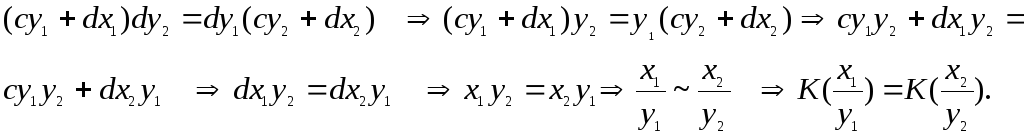
Определение: Частным от деления рационального числа K() на рациональное число K() ≠ 0, называется рациональное число K(), удовлетворяющее уравнению:

K() * K() = K()

В дальнейшем будем использовать обозначение:

K() : K() = K()

Теорема: Частное от деления любого рационального числа K() на рациональное число K()≠ 0 существует и единственно.

Доказательство:

I. Существование.

а) Определим вид частного двух рациональных чисел.

По определению K() : K() = K() K() * K() = K().

K() * K() = K()  K() = K()  ~  cxb = dya или xbc =yad, это означает, что ~ , то есть K() = K().Таким образом, вид частного определили.

б) покажем, что это число является частным от деления рационального числа K() на K(). Тогда должно выполняться равенство: K() * K() = K().

K() * K() = K() = K(), так как ~ .

Итак, существование доказано.

II. Единственность.

Пусть существуют два частных K() и K() от деления рационального числа K() на K() ≠ 0. Тогда выполняются равенства:

K() * K() = K() (1) K() = K()

K() * K() = K() (2) K() = K()

K() = K() ~ ~ K() = K().

Следствие: Частное рациональных чисел находится по формуле:

K() : K() = K().

Замечание: Операции сложения, умножения и деления на множестве (положительных рациональных чисел) определяется так же, как и наQ. Операция вычитания на существует не всегда.

Теорема: Для того, чтобы разность положительных рациональных чисел a и b существовала необходимо и достаточно, чтобы b < a.

(доказательство аналогично теореме на N)

Теорема: Сумма и произведение положительных рациональных чисел являются положительными рациональными числами.

Пусть рациональное число K() задается дробью ;

K() задается дробью .

1. Так как K() положительное, то a > 0 и b > 0 (1) ab > 0. Аналогично cd > 0 (2). Умножим (1) на d² >0, а (2) на b² >0

abd² >0 и cdb² >0 сложим их: abd² + cdb² >0 (ad+cb)bd >0 . Тогда

>0 , но =++>0, ч.т.д.

2. Если ab>0 и cd>0 , то (ab)(cd)>0 (ac)(bd)>0  *>0, ч.т.д.