
- •Методические указания к выполнению контрольной работы № 2
- •120700 Землеустройство и кадастры
- •Введение
- •Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.
- •1 Дифференциальные уравнения, их порядок, общий и частные интегралы
- •1.2 Дифференциальные уравнения второго порядка
- •Числовые ряды
- •2.1 Знакоположительные ряды
- •2.2 Знакопеременные ряды
- •2.3 Функциональные ряды
- •Варианты индивидуальных заданий
- •1. . 2..
- •Экстремум функции нескольких переменных
- •Градиент. Производная по направлению
- •5 Двойные интегралы
- •5.1 Основные понятия и определения
- •5.2 Основные свойства двойного интеграла
- •6 Элементы теории вероятностей
- •6.1 Случайные величины
- •6.1.1 Дискретные случайные величины
- •6.1.2 Числовые характеристики дискретной случайной величины
- •6.1.3 Непрерывные случайные величины
- •1) При;
- •2) При.
- •7 Варианты заданий
6.1.3 Непрерывные случайные величины
Для непрерывной
случайной величины, в отличие от
дискретной, нельзя построить таблицу
распределения. Поэтому непрерывные
случайные величины описывают другим
способом. Пусть задана непрерывная
случайная величина с возможными
значениями из интервала
![]() и
и![]() - действительное число. Под
- действительное число. Под![]() понимается событие «случайная величина
понимается событие «случайная величина![]() приняла значение, меньшее
приняла значение, меньшее![]() .
.
Интегральной
функцией распределения (или кратко
функцией распределения) непрерывной
случайной величины называется функция
![]() ,
равная вероятности того, что
,
равная вероятности того, что![]() приняла значение, меньшее
приняла значение, меньшее![]() :
:
![]() .
.
Отметим, что для дискретных случайных величин функция распределения определяется точно также.
Свойства интегральной
функции распределения
![]() :
:
1.
![]()
2.
![]() -
неубывающая функция, т.е. если
-
неубывающая функция, т.е. если![]() ,
то
,
то![]()
3. Вероятность
попадания случайной величины
![]() в полуинтервал
в полуинтервал![]() равна разности значений функции
распределения на правом и левом концах
полуинтервала
равна разности значений функции
распределения на правом и левом концах
полуинтервала![]() :
:
![]() .
.
4. Вероятность
того, что непрерывная случайная величина
![]() примет какое-либо заранее заданное
значение, равна нулю:
примет какое-либо заранее заданное
значение, равна нулю:
![]() .
.
5. Вероятности попадания непрерывной случайной величины в интервал, сегмент и полуинтервал с одними и те ми же концами одинаковы:
![]() .
.
6.Если возможные
значения случайной величины
![]() принадлежат интервалу
принадлежат интервалу![]() ,
то:
,
то:
1) При;
2) При.
Дифференциальная функция распределения
Дифференциальной
функцией распределения непрерывной
случайной величины
![]() (или ее плотностью вероятности) называется
функция
(или ее плотностью вероятности) называется
функция![]() ,
равная производной интегральной
функции:
,
равная производной интегральной
функции:
![]() .
.
Так как
![]() -
неубывающая функция, то
-
неубывающая функция, то![]() .
.
Теорема. Вероятность
попадания непрерывной случайной
величины
![]() в интервал
в интервал![]() равна определенному интегралу от
дифференциальной функции распределения
величины
равна определенному интегралу от
дифференциальной функции распределения
величины![]() ,
взятому в пределах от
,
взятому в пределах от![]() до
до![]() :
:
![]() .
.
Математическим
ожиданием непрерывной случайной
величины
![]() с плотностью вероятности
с плотностью вероятности![]() называют величину несобственного
интеграла (если он сходится):
называют величину несобственного
интеграла (если он сходится):
![]() .
.
Если случайная
величина определена на отрезке
![]() ,
то
,
то
![]() .
.
Дисперсией
непрерывной случайной величины
![]() ,
математическое ожидание которой
,
математическое ожидание которой![]() ,
а функция
,
а функция![]() является ее плотностью вероятности,
называется величина несобственного
интеграла (если он сходится):
является ее плотностью вероятности,
называется величина несобственного
интеграла (если он сходится):
![]() .
.
Дисперсию непрерывной случайной величины можно вычислить также по формуле
![]() .
.
Если случайная
величина определена на отрезке
![]() ,
то
,
то
![]() .
.
Для непрерывной случайной величины среднее квадратическое отклонение определяется также, как и для дискретной:
![]() .
.
Свойства числовых характеристик непрерывной случайной величины совпадают со свойствами дискретной случайной величины.
Пример 21. .Непрерывная случайная величина Х задана интегральной функцией распределения
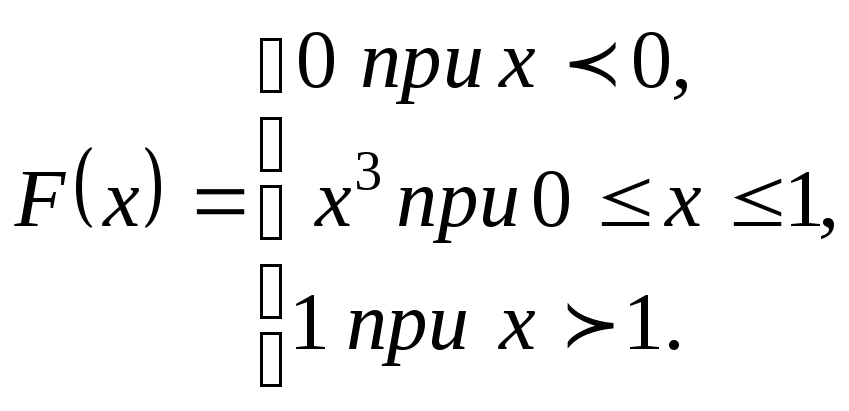
Найти: 1) дифференциальную функцию распределения f(x); 2) математическое ожидание М(Х) ;3) дисперсию D(X).
Решение. 1) Дифференциальной функцией распределения f(x) непрерывной случайной величины X называется производная от интегральной функции распределения F(x), то есть
![]()
Искомая дифференциальная функция имеет следующий вид :
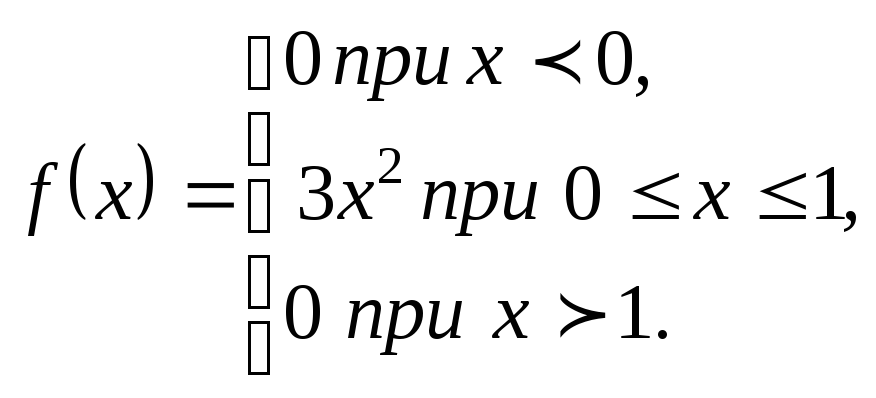
2) Если непрерывная случайная величина Х задана функцией f(x), то ее математическое ожидание определяется формулой
![]()
Так
как функция f(x)
при
![]() и при
и при![]() равна нулю, то из последней формулы
имеем
равна нулю, то из последней формулы
имеем
![]()
3) Дисперсию D(X) определим по формуле
![]()
Тогда

Закон нормального распределения вероятностей
Закон распределения
вероятностей непрерывной случайной
величины называется нормальным, если
ее дифференциальная функция
![]() определяется формулой
определяется формулой
 ,
,
где параметр
![]() ,
,![]() .
.
Нормальное
распределение с параметрами
![]() и
и![]() называют нормированным. Дифференциальная
функция в случае такого распределения
называют нормированным. Дифференциальная
функция в случае такого распределения
![]() .
.
Функция
![]() - четная, т.е.
- четная, т.е.![]() .
Значения этой функции можно найти в
специальной таблице.
.
Значения этой функции можно найти в
специальной таблице.
Если случайная
величина
![]() распределена по нормальному закону,
то вероятность того, что
распределена по нормальному закону,
то вероятность того, что![]() примет значение из интервала
примет значение из интервала![]() ,
вычисляется по формуле
,
вычисляется по формуле
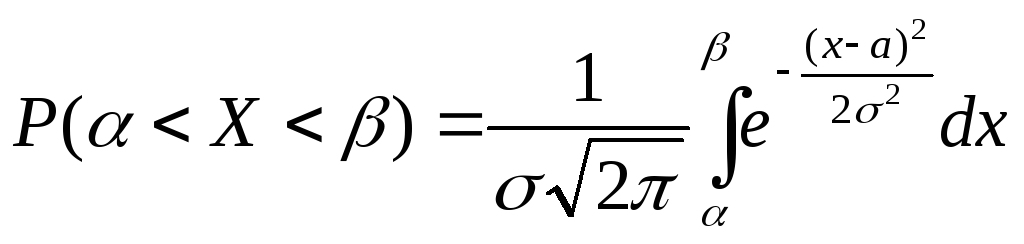
или
![]() ,
,
где
![]() - интегральная функция Лапласа. Значения
этой функции можно найти в таблице.
Интегральная функция Лапласа является
нечетной, т.е.
- интегральная функция Лапласа. Значения
этой функции можно найти в таблице.
Интегральная функция Лапласа является
нечетной, т.е.![]() .
.
Часто требуется
вычислить вероятность того, что
отклонение нормально распределенной
случайной величины
![]() от ее математического ожидания по
от ее математического ожидания по
абсолютной величине
меньше заданного числа
![]() ,
т.е. найти
,
т.е. найти![]() .
Эта вероятность находится по формуле
.
Эта вероятность находится по формуле
![]() .
.
Пример 22. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 40 мм и средним квадратическим отклонением 3 мм.
Найти: 1) вероятность того, что длина произвольно взятой детали будет больше 34 мм и меньше 43 мм; 2)вероятность того, что длина детали отклонится от ее математического ожидания не более чем 1,5 мм.
Решение.
1) Пусть X-
длина детали. Если случайная величина
Х задана дифференциальной функцией
f(x),
то вероятность того, что Х примет
значения, принадлежащие отрезку
![]() ,
определяется по формуле
,
определяется по формуле
![]()
Вероятность
выполнения строгих неравенств
![]() определяется той же формулой.
определяется той же формулой.
Если случайная величина Х распределена по нормальному закону, то
![]()
где
Ф(x)-
функция Лапласа,
![]()
В
задаче а=40,![]() Тогда
Тогда

2)
По условию задачи
![]() ,
где
,
где![]()
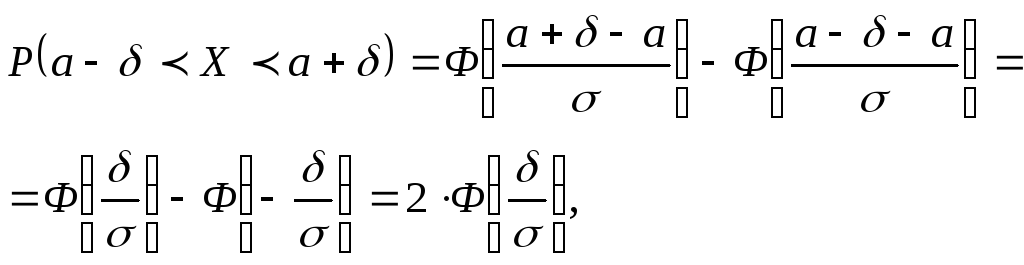
то есть
![]() .
.
Следовательно![]()
