
- •Методические указания к выполнению контрольной работы № 2
- •120700 Землеустройство и кадастры
- •Введение
- •Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.
- •1 Дифференциальные уравнения, их порядок, общий и частные интегралы
- •1.2 Дифференциальные уравнения второго порядка
- •Числовые ряды
- •2.1 Знакоположительные ряды
- •2.2 Знакопеременные ряды
- •2.3 Функциональные ряды
- •Варианты индивидуальных заданий
- •1. . 2..
- •Экстремум функции нескольких переменных
- •Градиент. Производная по направлению
- •5 Двойные интегралы
- •5.1 Основные понятия и определения
- •5.2 Основные свойства двойного интеграла
- •6 Элементы теории вероятностей
- •6.1 Случайные величины
- •6.1.1 Дискретные случайные величины
- •6.1.2 Числовые характеристики дискретной случайной величины
- •6.1.3 Непрерывные случайные величины
- •1) При;
- •2) При.
- •7 Варианты заданий
Варианты индивидуальных заданий
Задание 1.
Найти общий интеграл уравнения
.
1.
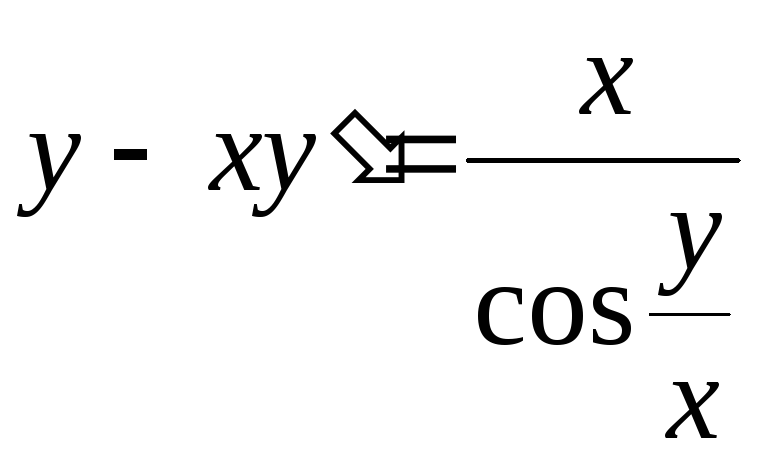 .
.
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
Задание 2.
Найти частное решение (частный интеграл) уравнения.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
Задание 3.
Найти общее решение дифференциального уравнения.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
Задание 4.
Найти общее решение дифференциального уравнения.
1.
![]() 11.
11.![]()
2.
![]() 12.
12.![]()
3.
![]() 13.
13.![]()
4.
![]() 14.
14.![]()
5.
![]() 15.
15.![]()
6.
![]() 16.
16.![]()
7.
![]() 17.
17.![]()
8.
![]() 18.
18.![]()
9.
![]() 19.
19.![]()
10.
![]() 20.
20.
![]()
Задание 5.
Написать три первые члены ряда. Найти интервал сходимости и исследовать ряд на сходимость на концах интервала.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
Задание 6.
Вычислить определенный интеграл с точностью до 0,001 путем разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.
1. . 2..
3.
![]() . 4.
. 4.![]() .
.
5.
![]() . 6.
. 6.![]() .
.
7.
![]() . 8.
. 8.![]() .
.
9.
![]() . 10.
. 10.![]() .
.
11.
![]() . 12.
. 12.![]() .
.
13.
![]() . 14.
. 14.![]() .
.
15.
![]() . 16.
. 16.![]() .
.
17.
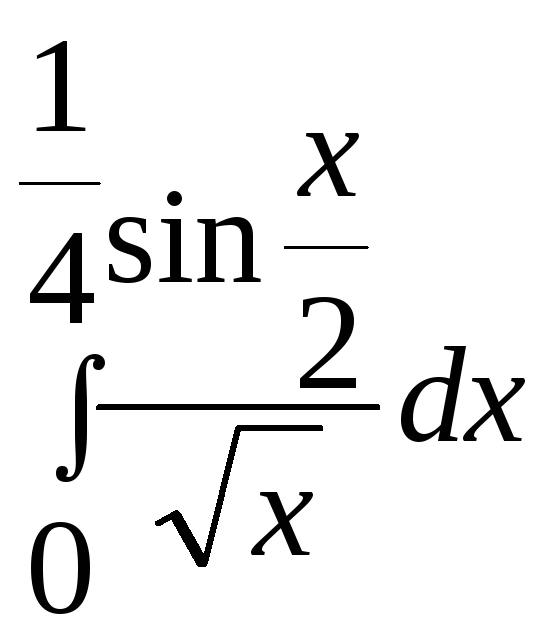 . 18.
. 18.![]() .
.
19.
 .
20.
.
20.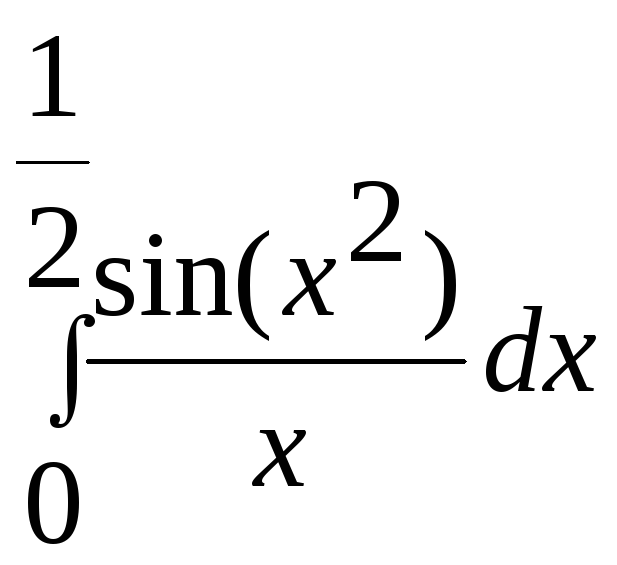 .
.
Функции нескольких переменных
Пусть задано
множество
![]() упорядоченных пар чисел
упорядоченных пар чисел![]() .
Соответствие
.
Соответствие![]() ,
которое каждой паре чисел
,
которое каждой паре чисел![]() сопоставляет
одно и только одно число
сопоставляет
одно и только одно число![]() ,
называется функцией двух переменных,
определенной на множестве
,
называется функцией двух переменных,
определенной на множестве![]() со значениями в
со значениями в![]() ,
и записывается в виде
,
и записывается в виде![]() .
.
Частной производной
функции нескольких переменных называется
производная функции одной из этих
переменных при условии постоянства
значений остальных переменных.
Обозначения частных производных:
![]() .
.
Частные производные
![]() называют частными производными первого
прядка. Их можно рассматривать как
функции от
называют частными производными первого
прядка. Их можно рассматривать как
функции от![]() .
Эти функции также могут иметь частные
производные, которые называются частными
производными второго порядка. Они
определяются и обозначаются следующим
образом:
.
Эти функции также могут иметь частные
производные, которые называются частными
производными второго порядка. Они
определяются и обозначаются следующим
образом:
![]()
![]()
![]()
Частные производные второго или более высокого порядка, взятые по различным переменным, называются смешанными частными производными.
Теорема. Если частные производные непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.
В частности, для
![]() имеем:
имеем:![]()
Пример 13.
Найти производные первого порядка и
смешанную производную второго порядка
функции
![]() .
.
Решение.
При нахождении частной производной
по
![]() полагаем
полагаем![]() постоянной:
постоянной:![]() .
При нахождении частной производной по
.
При нахождении частной производной по![]() полагаем
полагаем![]() постоянной:
постоянной:![]() .
.![]() .
.
Экстремум функции нескольких переменных
Пусть функция
![]() определена в некоторой области
определена в некоторой области![]() ,
точка
,
точка![]() .
.
Точка
![]() называется точкой максимума (минимума)
функции
называется точкой максимума (минимума)
функции![]() ,
если существует такая
,
если существует такая![]() -окрестность
точки
-окрестность
точки![]() ,
что для каждой точки
,
что для каждой точки![]() ,
отличной от
,
отличной от![]() ,
из этой окрестности выполняется
неравенство
,
из этой окрестности выполняется
неравенство![]() (
(![]() ).
).
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называются ее экстремумами.
Теорема
(необходимые условия экстремума). Если
в точке
![]() дифференцируемая
функция
дифференцируемая
функция![]() имеет экстремум, то ее частные производные
в этой точке равны нулю:
имеет экстремум, то ее частные производные
в этой точке равны нулю:
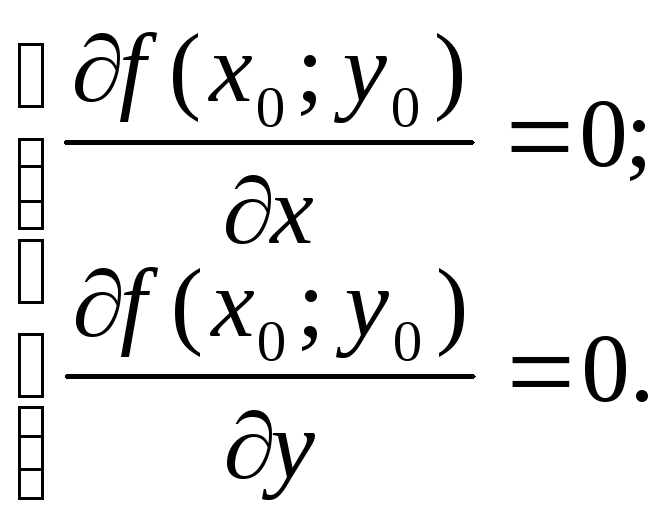
Точка, в которой частные производные первого порядка равны нулю, называется стационарной точкой функции.
Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.
Теорема
(достаточное условие экстремума). Пусть
в стационарной точке![]() и
некоторой ее окрестности функция
и
некоторой ее окрестности функция![]() имеет
непрерывные частные производные до
второго порядка включительно. Вычислим
в точке
имеет
непрерывные частные производные до
второго порядка включительно. Вычислим
в точке![]() значения
значения
![]() .
.
Обозначим
![]() .
.
Тогда:
1. Если
![]() ,
то функция
,
то функция![]() имеет в точке
имеет в точке![]() экстремум:
максимум, если
экстремум:
максимум, если![]()
![]() ;
минимум, если
;
минимум, если![]()
![]() .
.
2.Если
![]() ,
то функция
,
то функция![]() в
точке
в
точке![]() экстремума
не имеет.
экстремума
не имеет.
В случае
![]() необходимы дополнительные исследования.
необходимы дополнительные исследования.
Пример 14.
Найти экстремум функции
![]()
![]()
Решение.
Здесь
![]() ;
;![]() .
Точки, в которых частные производные
не существуют, отсутствуют.
.
Точки, в которых частные производные
не существуют, отсутствуют.
Найдем стационарные точки, решая систему уравнений:

Отсюда получаем точки М1 (6;3) и М2 (0;0).
Находим частные производные второго порядка данной функции:
![]() ,
,
![]() ,
,![]() .
.
В точке М1
(6;3) имеем:
А=-18, В=36, С=-108, отсюда
![]()
![]() =648,
т.е.
=648,
т.е.![]() >
0.
>
0.
Так как А<0, то в точке М1 функция имеет локальный максимум:
![]() =324
– 216 – 81 = 27.
=324
– 216 – 81 = 27.
В точке М2(0;0):
А=0, В=0, С=0 и, значит,
![]() =0.
Проведем дополнительное исследование.
Значение функции
=0.
Проведем дополнительное исследование.
Значение функции
![]() в
точке М2
равно нулю:
в
точке М2
равно нулю:
![]() (0;0)=0.
Можно
(0;0)=0.
Можно
заметить, что
![]() <
0 при
<
0 при
![]() ;
;![]() ≠
0;
≠
0;![]() при
при
![]() ,
,![]() .Значит, в
окрестности точки М2(0;0)
функция
.Значит, в
окрестности точки М2(0;0)
функция
![]() принимает
как отрицательные, так и положительные
значения. Следовательно, в точке М2
функция экстремума не имеет.
принимает
как отрицательные, так и положительные
значения. Следовательно, в точке М2
функция экстремума не имеет.
