2.1 Знакоположительные ряды

Для числовых рядов с положительными членами , при исследовании сходимости используются следующие достаточные признаки.

Интегральный признак Коши

Ряд с положительными убывающими членами сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл, где -непрерывная убывающая функция.

Нижним пределом несобственного интеграла может быть любое числоиз области определения . Этим признаком можно пользоваться, когда выражение общего члена имеет смысл не только для целых положительных значенийn но и для всех n, больших некоторого положительного числа т.

Пример 7.

Исследовать сходимость гармонического ряда:

Решение:

Заменяем в выражении общего члена номерn непрерывной переменно и убеждаемся, что является непрерывной убывающей функции при Вычислим несобственный интеграл

.Несобственный интеграл расходится, следовательно, расходится и гармонический ряд.

Признак Даламбера

Если ,то при q<1ряд сходится, а при q>1расходится. При q=1 вопрос о сходимости ряда остается нерешенным.

Пример 8.

Исследовать на сходимость ряд

Решение:

.

Применим признак Даламбера:

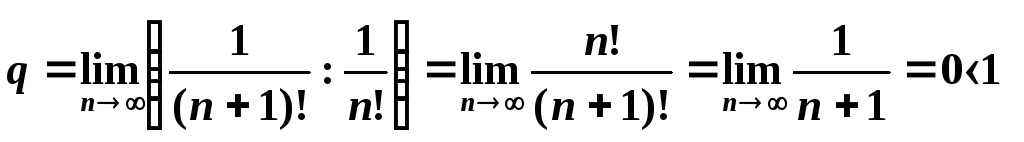.Так как то по признаку Даламбера исследуемый ряд сходится.

Признак сравнения

Пусть даны два ряда с положительными членами

… (а)

… (б)

если начиная с некоторого номера n:

1)и ряд (б) сходится, то и ряд (а) также сходится;

2)и ряд (б) расходится, то и ряд(а) также расходится.

При использовании этого признака исследуемый ряд часто сравнивается либо с бесконечной геометрической прогрессией , которая присходится, а прирасходится, либо с гармоническим рядом.

Пример 9

Исследовать ряд на сходимость с помощью признака сравнения

Решение:

Каждый член данного ряда, начиная со второго, больше соответствующего члена гармонического ряда: ,и, так как гармонический ряд расходится, то, согласно признаку сравнения, исходный ряд также расходится.

2.2 Знакопеременные ряды

Если знаки членов ряда (1) строго чередуются, то ряд называется знакочередующимся (знакопеременным).

Знакопеременный ряд (2) называется абсолютно сходящимся если ряд,

(3), составленный из абсолютных значений его членов сходится.

Знакопеременный сходящийся ряд (2) называется условно сходящимся, если ряд (3) расходится.

Всякий абсолютно сходящийся ряд есть ряд сходящийся.ъ

Признак Лейбница

Знакочередующийся ряд ,сходится, если его члены убывают по абсолютному значению, стремясь к нулю, т.е. еслии.

Пример 10. Доказать сходимость ряда

Решение :

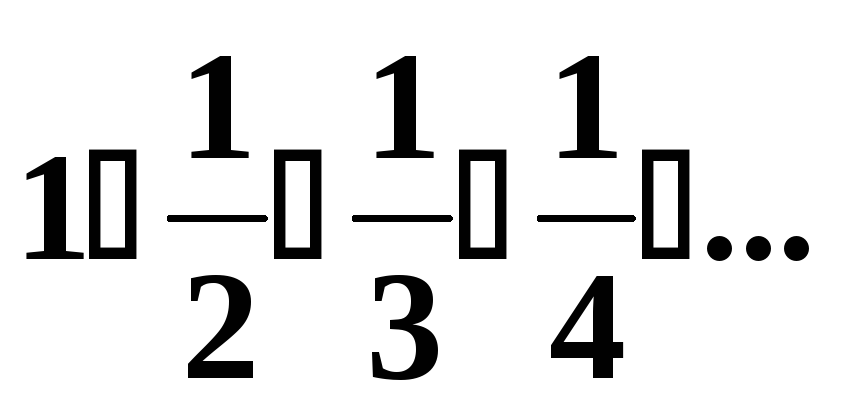, . Условия признака Лейбница выполняются, следовательно ряд сходится.

2.3 Функциональные ряды

Ряд , члены которого являются функциями от переменной, называется функциональным.

При различных значениях получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.

Совокупность значений , при которых функциональный ряд сходится, называется его областью сходимости.

Из всех функциональных рядов простейшими и наиболее употребительными являются степенные ряды вида

(4)

или(5)

Областью сходимости всякого степенного ряда является интервал числовой оси, симметричный относительно точки (для ряда (4)) или(для ряда (5)), который может быть закрытым, открытым или полуоткрытым.

Для определения области сходимости обычно вначале используется признак Даламбера, а затем те значения , для которых этот признак не решает вопроса о сходимости ряда, исследуется с помощью других признаков сходимости

Пример 11. Найти область сходимости ряда .

Решение:

далее по признаку Даламбера ищем

И определяем, при каких х этот ряд будет сходиться: .

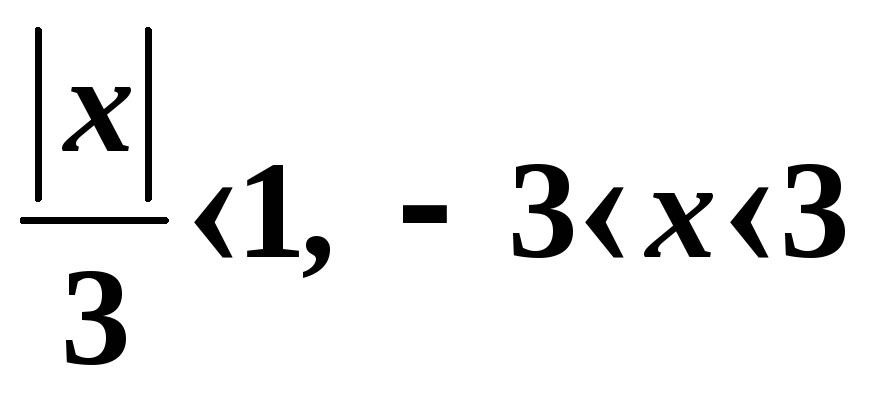При получаем ряд, который сходится по признаку Лейбница (см. пример 10).

При получаем гармонический ряд, который, как известно, расходится. Таким образом, интервалом сходимости данного степенного ряда является полуоткрытый интервал.

Ряды Тейлора

Рядом Тейлора для функции в окрестности точкиа называется степенной ряд относительно (х-а):

При а=0 ряд Тейлора есть степенной ряд относительно независимой переменной х:

который принято называть рядом Маклорена.

Разложение в ряд Маклорена некоторых функций

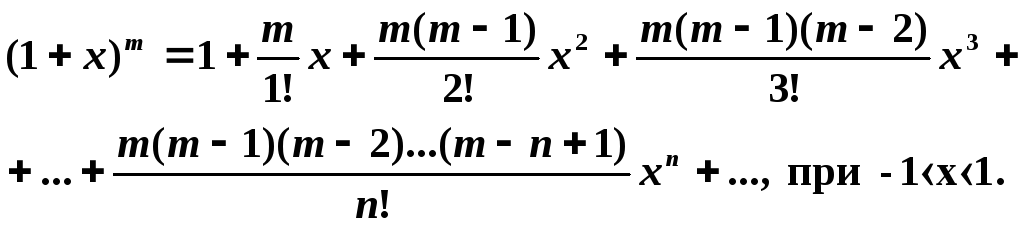
Применение рядов к приближенным вычислениям

Для вычисления приближенных значений функций с заданной точностью удобно пользоваться рядами в том случае, когда соответствующий ряд является знакочередующимся; для знакочередующегося ряда легко оценить погрешность приближенного значения суммы - она меньше абсолютного значения первого из отброшенных членов.

Пример 12. Вычислить с точностью до 0,001.

Решение:

Разложим подынтегральную функцию в степенной ряд и затем почленно проинтегрируем полученный сходящийся ряд в указанных пределах.

Заменив в разложении функции , получим искомое разложение:

Следовательно,

=

Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница. Так как шестой член этого ряда по абсолютной величине меньше 0,001, то достаточно взять сумму первых пяти членов.

Итак,