6

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Кафедра оптимизации систем управления

САМОСТОЯТЕЛЬНАЯ РАБОТА № 4

Интерпретация задачи линейного программирования в пространстве условий

Выполнила

Студентка О.В.Морланг

IV курс, группа 8512

« 27 » ноября 2004 г.

Проверил

В.Г.Ротарь

«__» _______ 200 __ г.

Томск, 2004

4.1. Сформировать задачу раскроя материалов из СРС-3 с матрицей условий размерностью [2;5].

Ограничения из самостоятельной работы № 3 выглядят следующим образом:

6*Х₁ + 4*Х₂ + 6*Х₃ + 2*Х₄ + 13*Х₅ = 1605;

6*Х₁ + 5*Х₂ + 10*Х₃ + 8*Х₄ + 2*Х₅ = 1302;

Целевая функция:

Z(x) = X₁ + X₂ + X₃ + X₄ + X₅  min

4.2. Решить задачу линейного программирования размерностью [2;5] геометрически в пространстве условий, когда уравнения ограничений записаны в канонической форме (в виде равенства).

U₁ = 6*Х₁ + 4*Х₂ + 6*Х₃ + 2*Х₄ + 13*Х₅ = 1605;

U₂ = 6*Х₁ + 5*Х₂ + 10*Х₃ + 8*Х₄ + 2*Х₅ = 1302

U₃ = X₁ + X₂ + X₃ + X₄ + X₅  min(max)

4.3. Найти решение задачи линейного программирования проекции для двух сечений конуса:

4.3.1. Проекция сечения конуса плоскостью U₁ = b₁.

4.3.2. Проекция сечения конуса плоскостью U₂ = b₂.

Полученные результаты сравнить.

4.3.1. Проекция сечения конуса плоскостью U₁ = b_1.

Проекция (см.график 1) построена с помощью нахождения точек встречи конуса и плоскости U₁ = b_1. Для этого мы рассмотрели по одному лучу конуса, находя соответствующие значения X_i из равенства U₁, умножая их на соответствующие коэффициенты в U₂.

• Точки встречи луча с секущей плоскостью U₁:

1302; 1042; 781,2; 325,5; 8463.

• Точки встречи луча с секущей плоскостью U₀:

217; 260; 130; 163; 651.

• П

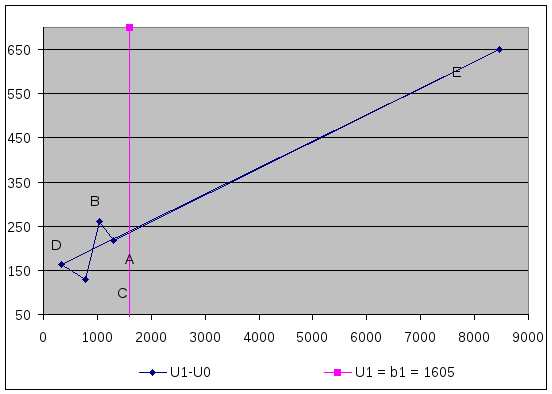
  График 1. Проекция сечения конуса плоскостью U₁ = b₁

  рямая U₁ = b₁= 1605.

Для нахождения точки минимума q и максимума Q найдём точки пересечения прямой U₁ с прямыми DЕ[(325,5; 163); (8643; 651)] и АЕ [(1302;217); (8643; 651)].

Составляем каноническое уравнение с неизвестной точкой Х:

(U1 – D1)/(E1-D1) = (X – D2)/(E2 – D2)

(1605 – 325,5)/(8463 – 325,5) = (X – 163)/(651 – 163)

X = 239,5

Точка Q имеет координаты (1605; 239,5).

(U1 – А1)/(E1-А1) = (X – А2)/(E2 – А2)

(1605 – 1302)/(8463 – 1302) = (Х – 217)/(651 – 217)

Х = 235,4

Точка q имеет координаты (1605; 235,4).

4.3.2. Проекция сечения конуса плоскостью U₂ = b_2.

Аналогично случаю 4.3.1.:

• Точки встречи луча с секущей плоскостью U₁:

1605; 2006,25; 2675; 6420; 246,9231.

• Точки встречи луча с секущей плоскостью U₀:

267; 401,25; 267,5; 802,5; 123,4615.

• П рямая U₂ = b₂= 1302.

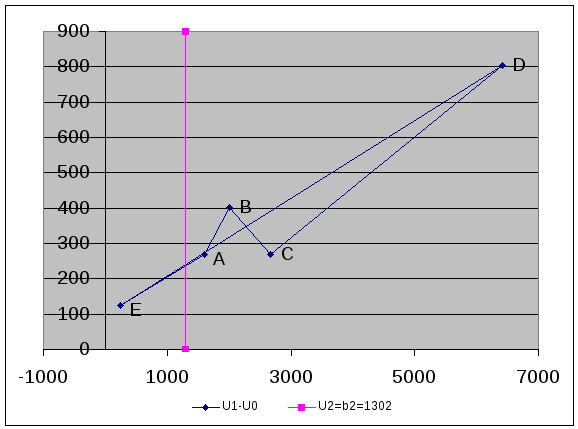
График 2. Проекция сечения конуса плоскостью U₂ = b₂

Для нахождения точки минимума q и максимума Q найдём точки пересечения прямой U₂ с прямыми ED[(246,9231; 123,4615); (6420; 802,5)] и EA [(246,9231; 123,4615); (1605; 267,5)].

Составляем каноническое уравнение с неизвестной точкой Х:

(U2 – E1)/(D1-E1) = (X – E2)/(D2 – E2)

(1302 – 246,9231)/(6420 – 246,9231) = (X – 123,4615)/(802,5 – 123,4615)

X = 235

Точка q имеет координаты (1302; 235).

(U2 – E1)/(A1-E1) = (X – E2)/(A2 – E2)

(1302 – 1302)/(8463 – 1302) = (Х – 217)/(651 – 217)

Х = 239,5

Точка Q имеет координаты (1302;239,5).

Сравнивая полученные значения, обнаружим, что целевая функция имеет максимумом и минимумом одни и те же точки, 239,5 и 235 соответственно, независимо от условий.

4.3.3. Найти качественное решение задачи линейного программирования при максимизации и минимизации целевой функции Z(х), определить структуру опорного плана (базиса) на основе геометрического представления.

Опорный базис:

6*Х₁ + 4*Х₂ + 2*Х₄ + 13*Х₅ = 1605;

6*Х₁ + 5*Х₂ + 8*Х₄ + 2*Х₅ = 1302;

При максимизации целевая функция достигает значения 239,52. Оптимальными переменными, при этом, являются Х₄ и Х₅.

При минимизации целевая функция достигает значения 235. Оптимальными переменными, при этом, являются Х₁ и Х₅.

4.3.4. Найти значения базисных переменных оптимального плана Х* и Z(Х*) для обоих случаев (max, min).

Для нахождения значений базисных переменных решаем следующие системы уравнений:

Для максимизации целевой функции:

2Х₄ + 13Х₅ = 1605;

8Х₄ + 2Х₅ = 1302.

Х₄ = 137,16; Х₅ = 102,36.

Z(X) = 239,52.

Для минимизации целевой функции:

6Х₁ + 13Х₅ = 1605;

6Х₁ + 2Х₅ = 1302.

Х₁ = 207; Х₅ = 28.

Z(X) = 235.

4.4. Решить задачу (max, min) для задачи, когда ограничения записаны в форме неравенства ().

U₁ = 6*Х₁ + 4*Х₂ + 6*Х₃ + 2*Х₄ + 13*Х₅ ≤ 1605;

U₂ = 6*Х₁ + 5*Х₂ + 10*Х₃ + 8*Х₄ + 2*Х₅ ≤ 1302;

U₃ = X₁ + X₂ + X₃ + X₄ + X₅  min(max).

Z(X)min = 0, т.к. Хi(i = 1,5) = 0.

Z(X)max = 239,52, т.к. Х₄ и Х₅, в нашем случае, равны 137,16 и 102,36 соответственно.

4.5. Записать аналитически уравнения задачи ЛП и отобразить в пространстве условий для следующих вариантов

4.5.1. А1 - единственное решений задачи линейного программирования

Случай, рассматриваемый в вышеприведённом решении.

4.5.2. А2 - бесконечное множество решений.

В данном случае рассматриваемая фигура конуса будет представлять собой прямую, с которой совпадает целевая функция. Строго через эту прямую проходит вектор ограничения. Все векторы линейно зависимы. В пространстве условий данный случай представляет точку (см. график 3). Максимум и минимум целевой функции в этом случае совпадают.

График 3. Бесконечное множество решений в пространстве условий

4.5.3. В1 – нет решения, целевая функция не ограничена сверху (max Z(x)) либо снизу (min Z(x)).

Полученная фигура (см.график 4) не ограничена либо снизу, либо сверху.

График 4. Неограниченная целевая функция в пространстве условий

4.5.4. В2 – система условий несовместна.

В этом случае мы имеем несовместимость условий, т.е. вектор ограничений не имеет общей области с пространством условий.