
- •Лекция № 4.
- •Преломление света на границе двух сред и пучка заряженных частиц на границе потенциалов
- •Потенциал аксиально-симметричного электростатического поля.
- •Движение параксиальных пучков электронов в аксиально-
- •Параметры увеличения в электронной линзе.
- •Геометрические параметры тонкой электростатической линзы.

Лекция № 4.
ЭЛЕКТРОННАЯ ОПТИКА.
Аналогия световой и электронной оптики. Электронная оптика параксиальных пучков. Движение заряженных частиц в аксиально- симметричном электрическом поле.
• Физическим обоснованием |
|
возможности построения |
|
аналогии прохождения |
|
электронного луча в |
|
электрическом поле с постепенно |
|
изменяющимся потенциалом и |
|
прохождения светового луча |
|
через среду с изменяющимся |
|
коэффициентом преломления |
|
(оптико-механическая аналогия) |
|
является общее сходство между |
|
обычной механикой и |
|
геометрической оптикой. И для |
|
движения материальной точки и |
|
для светового луча известен |
|
вариационный принцип |
t1 |
Гамильтона: |
Ldt 0 |
|
|
t0

Преломление света на границе двух сред и пучка заряженных частиц на границе потенциалов
•Покажем, что принцип Ферма эквивалентен закону преломления геометрической оптики Оптическая длина, ее вариация:
L l1n1 l2 n2
•,Lоткудаn1 следуетl1 n2 lзакон2 преломленияn1 x sin 1 n2 x sin 2 0 геометрической оптики:
• |
sin 1 |
n2 |
|
sin |
|
n |
|
|
Получим аналогичный закон для электронной |
2 |
1 |
оптики.Так как параллельная границе раздела |
|||
компонента скорости не меняется то |
|
|
|
Следовательно:
V1 sin 1 V2 sin 2
(где - ускоряющее напряжение)sin – зUакон
1  2
2
преломления электронной оптики. Таким образом, sin 2 U1
преломления.
- аналог показателя
показателя
 U
U
1 |
n1 |
||
|
l1 |
||
|
|
l2 |
|
|
|
2 |
n2 |
V1 |
x |
|
|
1 |
|
U1 |
|
|
|
|
|
+ |
+ |
+ |
+ |
- |
- |
- |
- |
U 2
2 V2

Потенциал аксиально-симметричного электростатического поля.
|
Задание преломляющих поверхностей в виде |
r |
|
U1 |
|
|
U 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
сеток затруднительно, поэтому часто |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
используют диафрагмы с аксиально- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
симметричным распределением потенциала U r, z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Потенциал удовлетворяет уравнению Лапласа: |
|
2 U |
|
|
|
1 |
|
|
U |
2 U |
|
0 |
|
|
|||||||||||||||||||||
|
|
r |
2 |
|
|
r r |
z 2 |
|
|
|
||||||||||||||||||||||||||
Так как U r, z |
= U r, z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
, то в результате разложения по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
будут только четные степени: U r, z b0 z b2 z r 2 b4 z r4 |
... b2k z r 2k |
|
|
|||||||||||||||||||||||||||||||||
С учетом |
2U |
2b2 z 12b4 z r |
2 |
30b6 z r |
4 |
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
U 2b |
|
z 4b z r 2 |
6b z r 4 ... |
|
2U |
b |
|
z |
|
r |
2 |
b |
|
z |
|
|
r |
4 |
|
|
|
... |
||||||||||||||
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
4 |
6 |
|
|
|
|
|
|
|
|
|
|
|
b z |
|
||||||||||||||||||
r r |
|
|
|
|
|
|
|
z 2 |
0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Получим распределение потенциала в пространстве в виде:
|
|
|
|
|
|
|
r |
|
1 |
r |
|
IV |
|
|
|
1 |
|
|
r |
6 |
IV |
|
|
|
|
|
k U |
2k |
|
z |
|
r |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2k |
|
||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
U |
r, z |
|
U |
z |
|
|
|
|
|
|
|
|
|
|
U |
|
|
z |
|
|
|
|
|
|
|
U |
z |
|
... |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
U (z) |
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
k ! |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Таким образом, распределение потенциала аксиально-симметричного поля определяется значением потенциала на оси .
Движение параксиальных пучков электронов в аксиально-
симметричном электростатическом поле.
Для приосевых электронов (r2/L2хар<< r/Lхар, где Lхар – характерная длина системы), которые еще называют
параксиальными, можно получить уравнение траектории. Так как , то электроны не вращаются вокруг оси z. Другие компоненты электрического поля определяются из соотношений:
U |
E |
|
U z |
|
|
|
r 4 |
U z |
|
U z |
|
|
|
|
|
|
||||||||
z |
|
4 |
|
|
|
|
|
|||||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
U |
|
Er |
r |
U |
z r3 |
U IV z |
|
r |
U z |
|
|
|
|
|
|||||||||
|
z |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
er |
|
|
||||
Уравнение движения для электрона: |
{mr eEr |
2 |
|
U |
z |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mz eU z |
|
|
||
Получим уравнение траектории r(z) параксиального пучка: |
|
|
|
|
||||||||||||||||||||
|
d 2 r |
U ' (z) dr |
|
|
U '' (z) |
|
|
|
|
которое называется основным |
|
|
|
|
||||||||||
|
dz 2 |
2U (z) dz |
|
|
4U (z) r 0 |
|
уравнением электронной оптики. |
|
||||||||||||||||

Параметры увеличения в электронной линзе.
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основное уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
электронной оптики является |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
однородным дифференциальным |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнением относительно r |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
второго порядка. Решение, как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B r |
||||
известно, можно представитьв |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
виде суммы двух частных |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
решений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
rA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|||||||||||||||||||||||||
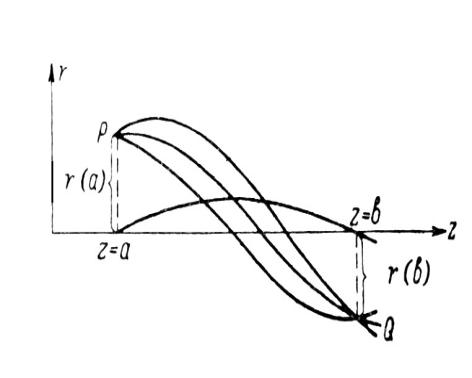
r z C1r1 z C2 r2 z |
A |
Предметная |
|
Плоскость |
|||||||||||||||||||||
|
|
плоскость |
|
изображени |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
я |
|||||
Пусть , частные решения при и |
Изображение в линзе. |
|
r z C1r1 z - это совокупность
траекторий, которые пересекают |
|
|
ось в точках А и В, т.е. в точке В |
||
соберутся все электроны, |
|
|
вышедшие из точки А U a |
r2 |
b |
U b |
r2 |
a |
C1r1 z C2 r2 z
|
|
|
|
A |
|
|
|
b |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
a |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
r b |
|
C1r1 z C2 r2 z |
|
|
B |
|||||
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
r a |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Тонкие электростатические линзы. |
|
|
||||
|
|
|
r(b) |
|
|
|
|
|
Линейное увеличение линзы: M r(a) |
, |
Угловое увеличение в линзе. |
|
|||||
где r(a) и r(b) расстояние до траектории от |
r |
|
|
|
||||
оси системы. Угловое увеличение линзы, |
|
|
|
|||||
определяемое как отношение тангенсов |
r ' (b) |
|
|
|
||||
углов наклона траектории к оси : G tg 2 |
|
z |
||||||
Из основного уравнения электронной |
tg |
r ' (a) |
1 |
|
|
|||
1 |
|
|
2 |
|||||
|
|
|
||||||
оптики можно получить соотношение |
|
|
|
|||||
между линейным и угловым увеличением |
|
|
|
|
||||
линзы |
|
M G |
U (a) |
|
Геометрические параметры линзы. |
|
||
|
|
U (b) |
|
|
h1 |
h |
|
|
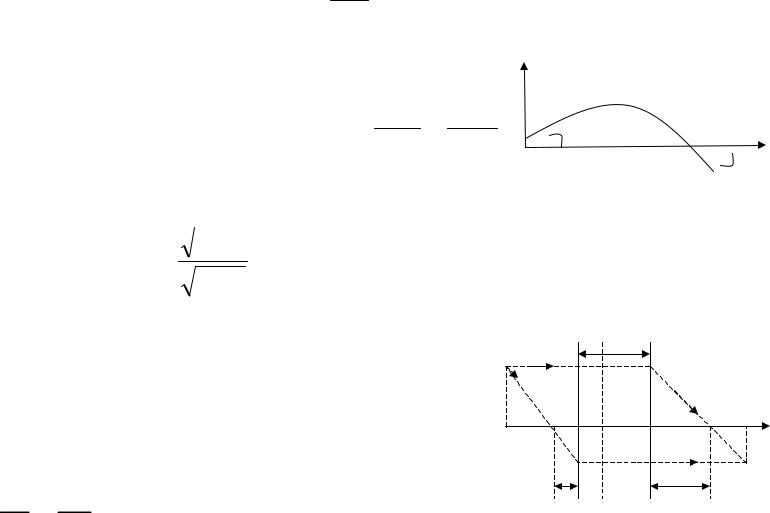
Рассмотрим тонкие линзы, главные |
|
|
|
|||||
|
r1 z |
|
2 |
|
||||
плоскости которых находятся при z = a и |
|
|
|
|
||||
при z = b. Для тонких линз расстояние |
|
r2 |
z |
|
|
|||
между главными плоскостями много |
|
b |
z |
|||||
меньше фокусных расстояний (b - a) << f1, |
a |
|
||||||
|
|
|
||||||
f2 , т. е. главные плоскости сливаются. |
|
|
|
|
|
|||
f1 f2 |
1 |
- основное соотношение тонкой |
f1 |
f2 |
|
|||
l1 |
l2 |
|
|
|||||
|
линзы. |
|
|
|
|
|
||
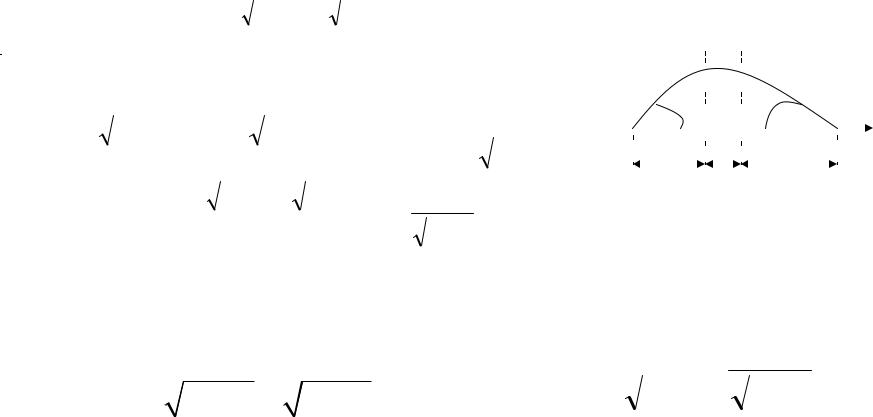
Геометрические параметры тонкой электростатической линзы.
Возьмем основное уравнение электронной
оптики в виде: |
|
|
|
|
|
|
d |
|
|
|
dr |
|
|
|
r |
U z |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
U z |
|
|
|
|
U z |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
dz |
|
|
|
|
|
|
|
|
|||||
Проинтегрируем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dr |
|
|
|
|
|
|
|
|
dr |
|
|
|
|
|
1 b r z U z |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
U b |
|
U a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
4 a |
|
|
|
|||||||||||||||||||||||
|
|
dz b |
|
|
|
|
|
|
|
|
dz |
|
a |
|
|
|
U z |
||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
U b |
|
|
|
|
|
U a |
|
|
1 b |
|
|
z |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 a |
|
|
dz |
||||||||
|
|
|
|
l2 |
|
|
|
|
|
|
|
l1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
U z |
|||||||||||||||
С учетом основного соотношения тонкой линзы: получим фокусные расстояния слева и справа:
1 |
|
1 |
b |
U z |
|
1 |
|
|
|
|
|
dz |
|
|
|
|
f2 |
|||
f |
4 U a |
U z |
||||
1 |
|
a |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
a |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|||||||||
A |
|
|
|
|
|
B |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 l2
|
|
|
f1 |
|
|
|
f2 |
1 |
|
||||||
|
|
|
l |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
l |
2 |
|
|
|
|
|
|
1 |
|
|
|
b |
|
|
|
|
|
|
|||||
1 |
|
|
|
U z |
|
|
|||||||||
|
|
|
|
|
|
a |
|
|
dz |
||||||
4 |
|
|
|
|
|
|
|||||||||
U b |
U z |
||||||||||||||
Для одиночной диафрагмы с круглым отверстием : |
1 |
|
Ez1 Ez 2 |
|
fD |
4U d |
|
|
|
