
|
1.1. Классификация волноведущих структур и направляемых волн. Р\ся направляемые эмв, а они могут существовать только при наличии направляющих элементов, совокупность которых образует направляющую систему энергии от передатчика к приёмнику. Др. название – линии передачи или волноведущие структуры. Линия передачи называется регулярной, если в поперечном сечении неизменны св-ва среды. Л.п. делятся на: Открытые л.п. – нет экрана, ограничений области распространения эмв, энергия которых распространяется во всё окружающее пространство, но основная часть энергии вблизи линии. Недостаток – влияние среды на характеристики линии; Закрытые л.п. – волноводы – обязательно есть одна или несколько поверхностей, ограничивающих область распространения ЭМВ в поперечном сечении. С точки зрения математического описания делятся: 1)Л.п., процессы в которых описываются методами теории цепей (телеграфные ур-я) – 2хпроводная линия, коаксиал; 2)Л.п., процессы в которых могут быть описаны только с помощью электродинамиКи экранированные волноводы, замедляющие системы – спиральные линии, периодически диафрагмируемые волноводы, диэлектрические волноводы и т.д. При выборе л.п. решающее значение имеет тип волны и критической частотой, при которой прекращается перенос |
1.2. Прямые волны – у которых фазовые и групповые скорости направлены в одну сторону, обратные – в противоположные. Иногда при определении поля в волноведущих хорошо проводящих структурах обычно идеализируют задачу заменяя металл идеальным проводником => легко найти поле в диэлектрике, и оно слабо отличается от существующего. Граничным условиям могут удовлетворять поля Е и Н независимо друг от друга и поля этих 2х классов могут существовать раздельно. Полное поле в регулярных линиях передачи это сумма независимых полей класса Е, Н, Т. В волноводах поперечное сечение которых односвязная область существование поля Т невозможно и полное поле сумма полей классов Е и Н. В симметричной 2х проводной линии – открытая линия передачи с идеальными парами канализация может быть только полями класса Т.
|
2.1.Волны в регулярных линияхпередач.Параметры постоянны вдоль оси z, а линия бесконечная. Среда, заполняющая линию однородная и без затухания. ЭМП, которые могут существовать в л.п. без внешнего источника определяются решением однородных ур-ий Максвелла. Используем МКА:
|
2.2.
учтя
|
2.3.
если
|
|
3.1.
Краевые задачи, электрические и
магнитные волны. Пусть волновод
без потерь из идеального
проводника, тогда нет
тангенсальной компоненты
электрического поля.
Р\м регулярную линию.
Касательная к цилиндрическим
стенкам будет z-ая
компонента
|
3.2.
Положив
Для поля класса
Е если
|
3.3. При
|
4.1.Перенос энергии вдоль волновода Поток энергии в волноводе определяется средним за период значением вектора Пойтинга (ВП)
|
4.2.
Анализ реальн.
пр-ти в 2 этапа: распространение
поля в поперечном сечении
отличается от распространения
в волноводе без потерь
только вблизи стенок. На
идеально проводящей
стенке нет касательной
составляющей поля Е. При
расчёте коэффициента
затухания касательной
составляющей пользуются
усл. Леонтовича. Для
результирующего поля
в диэлектрике амплитуды
полей:
|
|
5.1.Прямоугольный волновод . Волны Т здесь невозможны, но возможны волны Е и Н. Поперечные составляющие Е и Н выражены через продольные составляющие. Для каждой структуры поля в волноводе решим волновое ур-е Гельмгольца в ДСК:
|
5.2.
|
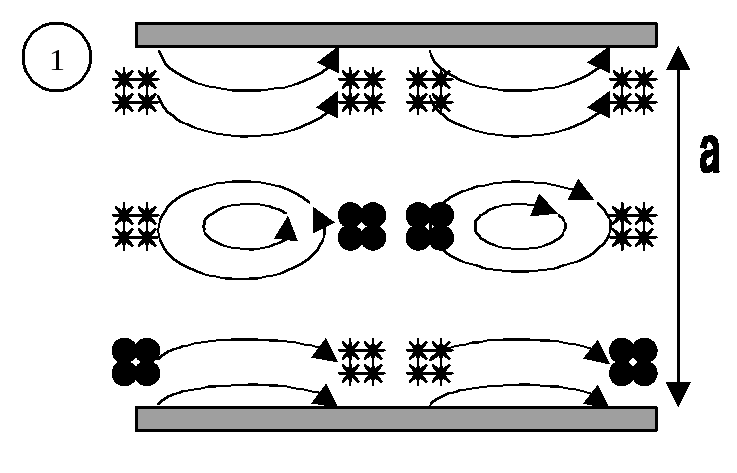
5.3. Для Е21:
В общем случае Emn, a-сторона и b-сторона делятся на m частей и n частей, затем в каждом квадрате строится E21. Нарисуем структуру поля Н:
|
5.4.
в волноводе распространяться
не будет, не будет передаваться
информация. Волны Hmn
и Emn которым будут
соответствовать
одинаковые
|
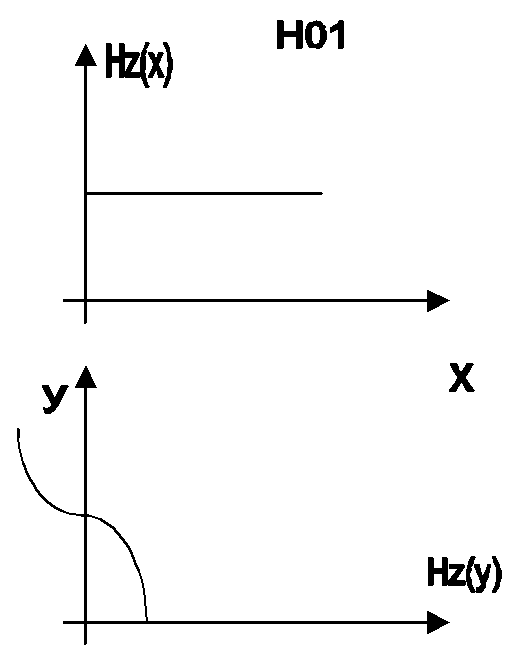
6.1. Куглый волновод.
Выберем ЦСК, z
направлена вдоль оси
волновода. Тогда ур.
Гельмгольца примет вид:
|
|
6.2.
Пусть m-тый корень
|
6.3.
Если
взять m=0 =>
|
7.1. Коаксиальный волновод Состоит
из 2х изолированных
проводников. В сечении
имеет вид кольца. Сечение
имеет вид двухсвязной области
=> могут существовать
независимо Е и Н и Т волны.
Т-волна явл-ся низшим типом
волны. Р\м Т-волну. Для Т-волны
поперечное
|
7.2. из
ГУ
|
8. Открытые линии передач. Низший тип волны, поперечная Т-волна. Анализ волн делается только численно, но можно её рассматривать как деформированную коаксиальную линию.
Диэлектрический волновод. Пусть радиус r=a, d=2a.
|
|
|
Поперечные
составляющие Е и Н выражаются
через продольные. Верхние
знаки соответствуют
падающей волне, а нижние
отражённой. Из (3)
|
странения,
a - коэффициент
затухания, b
- коэффициент фазы. “-”
– в положительном
направлении движения
волны, ”+” – в отрицательном.
Индекс S показывает
зависимость величины
только от поперечных
координат u и
v. (1) с учётом (2) и
(3) в поперечных
координатах.
|
|
энергии. Л.п. используется в режиме основной волны, у которой наименьшая критическая частота, но иногда передача осуществляется на высших типах волн. Направленные волны могут быть: поперечные, электрические, магнитные, смешанные. Фундаментальные типы: Поперечные или Т волны (составляющие Ez и Hz =0). Они есть только в л.п. с 2 и более изолированных проводников. Особенность – критическая частота =0. Электрические Е волны. (Ez ¹0 Hz=0) Существуют в волноводах с однородным диэлектрическим заполнением; Магнитные H волны. (Ez =0 Hz¹0) Зависит от форм, размера, поперечного сечения диэлектрика. LE волна – в поперечном сечении л.п. присутствует только одна составляющая электрического поля (продольно электрическая); LH волна – тоже, но продольно магнитная.; Гибридные волны НЕ и ЕН – векторы Е и Н имеют и продольные и поперечные составляющие. Н и Е существуют в волноводах с однородным диэлектрическим заполнением – их критические частоты ¹0 и зависит от формы и размеров поперечного сечения и параметров .заполняющего диэлектрика. LE и LH волны характерны для частично заполненных продольных волноводов: неоднородная среда и среда с пространственной дисперсией. Решается численным решением трансцендентных или диф. ур-ий |
|
и
поверхностный импеданс
диэлектрика. Для хорошо
проводящего металла:
Откуда
|
Из (1)
увеличение переносимой
мощности сопровождается
увеличением напряжённости
ЭП, но есть придел
|
v – коэффициент затухания. => Z – мнимая для Е полей оно имеет емкостной характер, а для Н полей индуктивный. Поперечные составляющие сдвинуты на 90 => колебательный характер движения энергии => в закритическом режиме нет переноса энергии, а вектор Пойтинга мнимый. Эл.м. процесс называется местным полем. Экспоненциальное затухание не связано с потерями эл.м. энергии т.к. рассматривался волновод без потерь. Такие местные поля существуют в качестве локальных полей, существующих в местах нерегулярностей.
|
Раскладывая
поперечные компоненту
по ортам
– фазовая скорость |
Для Е полей это
условие выполняется
автоматически, для полей
Н (1). Т.о. в волноводах с
идеально проводящими
границами раздела г.у.
могут удовлетворять полям
Е и Н независимо др. от
друга => независимое
существование полей
этих классов в волноводах.
Ур-е |
|
Для
Е волн: учитываяя
, (2) примет вид:
|
|
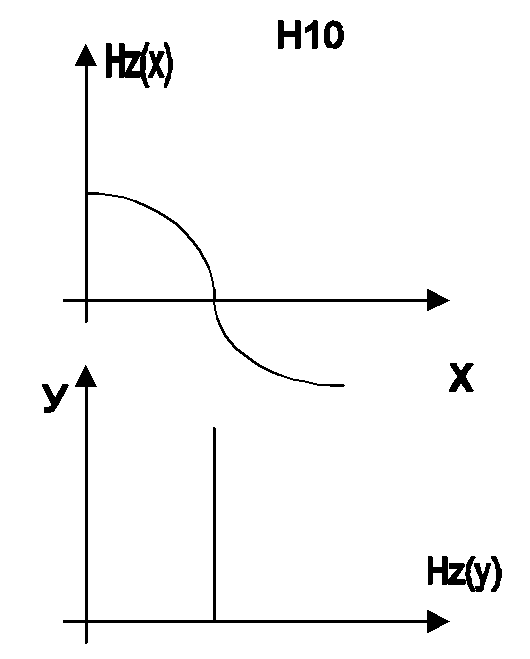
Низшим типом
Е волны явл-ся Е11, низшим типом
волн Н явл-ся Н10 b<a.
|
m
может=0.
|
:
Р\м Н волну. Г. у.:
|
|
|
волновое сопротивление линии
Первым высшим типом явл-ся Н11. Введение металлического стержня мало влияет на распределение магнитного поля Н11.
|
Р\м 2 случая: 1)m 0: m – целое тогда
2)m = 0
Касательная
составляющая Е на проводниках
должна быть =0:
|
|
Для
Н волн:
|

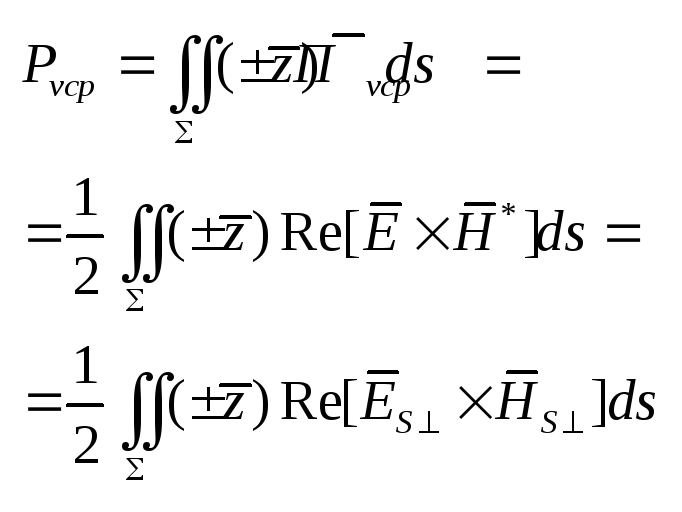 ,
- площадь
сечения волновода. Для
волновода без потерь
,
- площадь
сечения волновода. Для
волновода без потерь
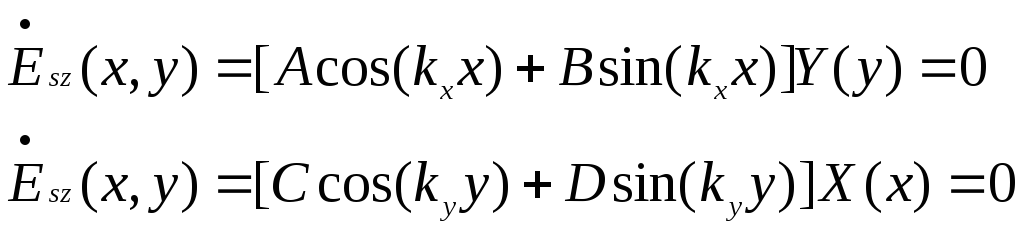

 (2)-
то же.
(2)-
то же.
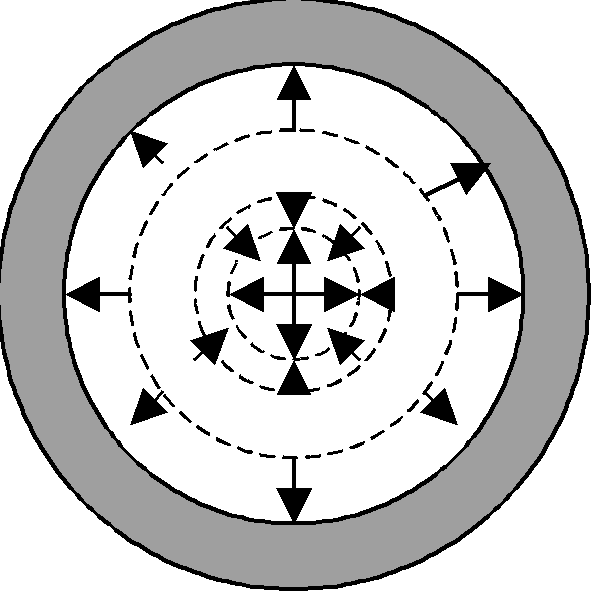
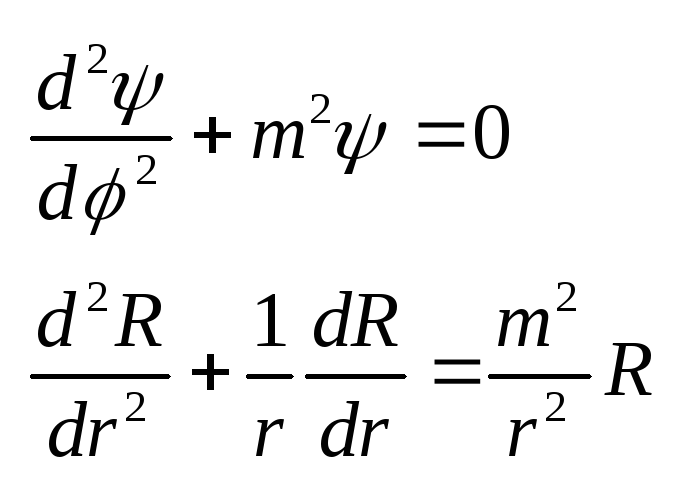 (2.28)
(2.28)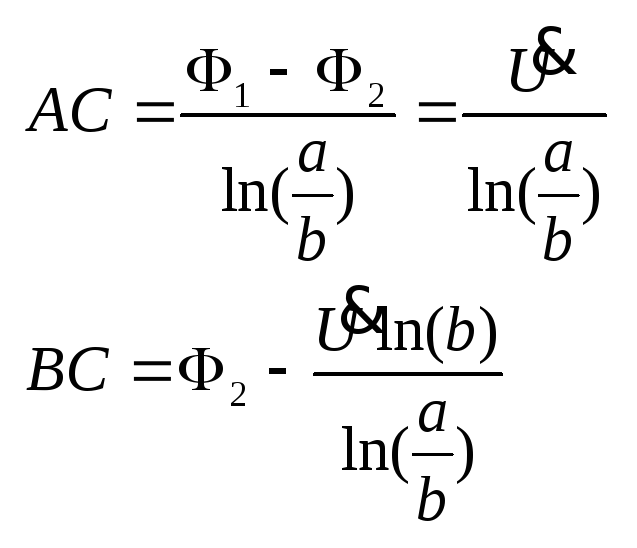 в результате:
в результате: Е в Т-волне направлено
только радиально, а Н в
Т-волне - азимутально. Для
Т-волны можно говорить о
полном токе и полном
напряжении:
Е в Т-волне направлено
только радиально, а Н в
Т-волне - азимутально. Для
Т-волны можно говорить о
полном токе и полном
напряжении: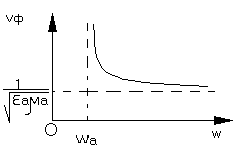
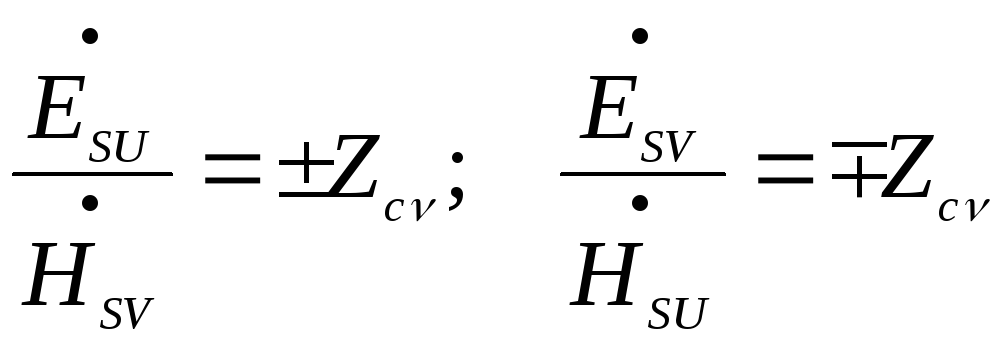 .
.
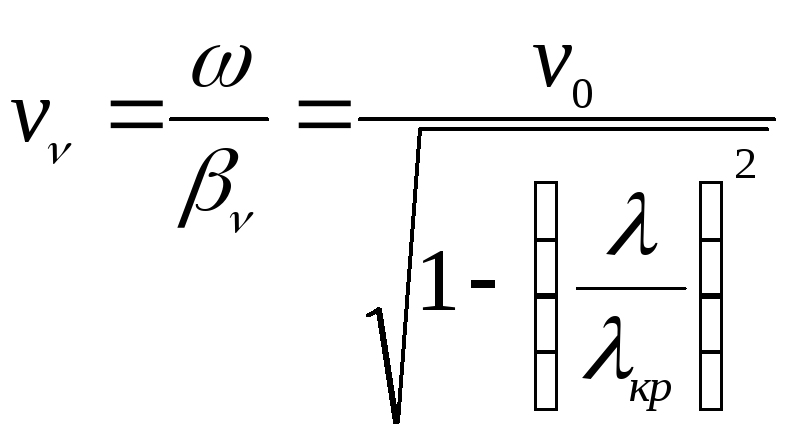
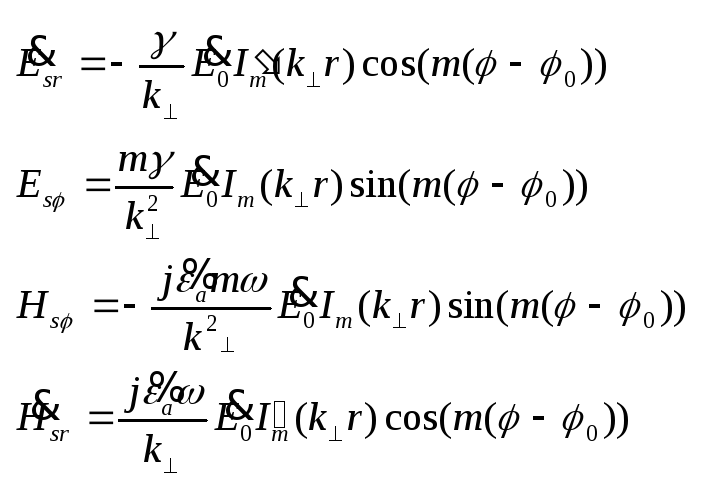 При Im
– дифференцируя по полному
её аргументу и найдём из
ГУ:
При Im
– дифференцируя по полному
её аргументу и найдём из
ГУ:
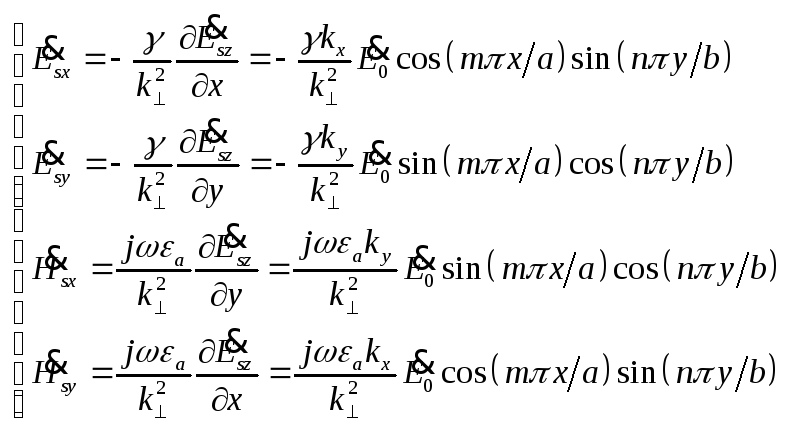 ,
причём
,
причём
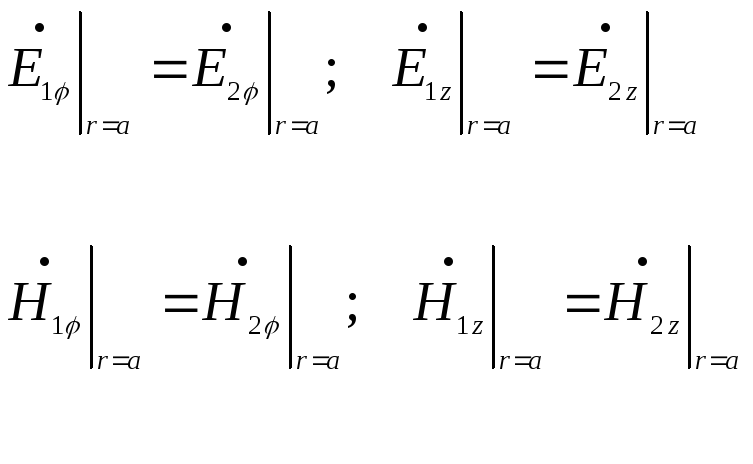
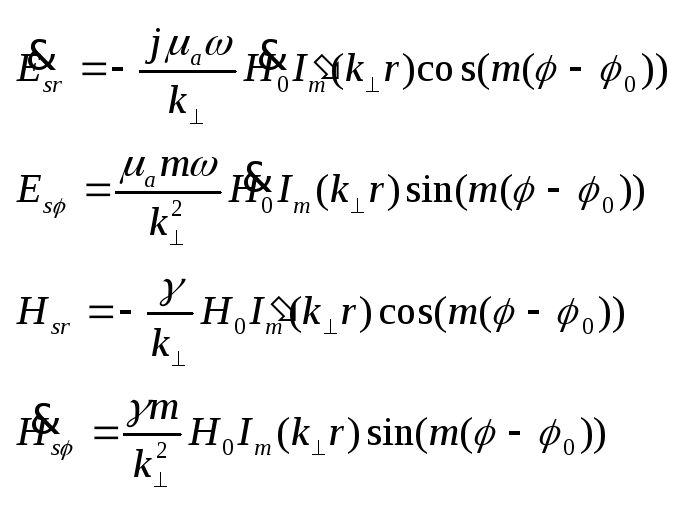 ГУ:
ГУ: