ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ВОРОНЕЖСКИЙ ИНСТИТУТ ВЫСОКИХ ТЕХНОЛОГИЙ

Центр дистанционных технологий

Кафедра физико-математической подготовки

Курс лекций

по дисциплине

Теория вероятностей, математическая статистика и случайные процессы

для студентов очной формы обучения

по направлению 230100

«Информатика и вычислительная техника»

Воронеж 2006

Лекция 1.

СЛУЧАЙНЫЕ СОБЫТИЯ И ДЕЙСТВИЯ НАД НИМИ. КЛАССИЧЕСКОЕ И СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ

Предмет теории вероятностей

Все события делятся на 3 группы (вида):

Достоверное – событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S.

Пример: при нормальном атмосферном давлении и t=20^оC событие «вода в стакане в жидком состоянии» достоверно.

Невозможное – событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий S.

Пример: событие «вода в стакане в твердом состоянии» при тех же условиях заведомо не произойдет.

Случайное – событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти.

Пример: если брошена монета, то событие «выпал орел» случайное.

Совокупность условий влияющих на выпадение орла: сила, с которой брошена монета, форма монеты и др.

Невозможно учесть действия всех этих причин на результат.

Теория вероятностей не ставит перед собой задачу предсказать событие.

Другое дело, если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т.е. речь идет о массовых однородных случайных событиях.

Достаточно большое число однородных случайных событий независимо от природы подчиняются определенным закономерностям, а именно вероятным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.

Предметом теории вероятностей является изучение вероятных закономерностей массовых однородных случайных событий.

Случайные события

«Совокупность условий S осуществлена» <=> «произведено испытание» т.е. событие будет рассматриваться как результат испытания.

Пример 1. Стрелок стреляет по мишени разделенной на четыре области. Выстрел – это испытание. Попадание в определенную область – событие.

Пример 2. В урне имеются цветные шары. Из урны наудачу берут один шар. Испытание – извлечение шара. Событие – появление шара определенного цвета.

События называются несовместимыми, если появление одного из них исключает появление других событий в одном и том же испытании.

Пример: Брошена монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» - несовместимые.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.

Если события, образующие полную группу, попарно несовместимы, то в результате испытания появится одно из этих событий.

Пример: Стрелок произвел выстрел по цели. Обязательно произойдет одно из двух следующих событий: попадание, промах. Эти два несовместимых события образуют полную группу.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Пример: Появление «герба» или «надписи» при бросании монеты – равновозможные события.

Пример: Появление того или иного числа очков на брошенной игральной кости – равновозможные события.

Классическое определение вероятности

Существует несколько определений вероятности. Рассмотрим пример:

Пусть в урне 6 одинаковых шаров: (тщательно перемешанных) 2 – красных, 3 – синих, 1 – белый. Очевидно, возможность вынуть из урны цветной (красный или синий) больше, чем белый. Можно ли охарактеризовать эту возможность числом?

Да. Это число называют вероятностью события. Т.е., вероятность – есть число, характеризующее степень возможности того, что взятый наудачу шар цветной. Обозначим, А – событие «появление цветного шара» Испытание – извлечение шара из урны. Каждый из возможных результатов испытания, назовем элементарным исходом (элементарным событием)

Элементарный исход:

- появляется белый шар;

- появляется красный шар;

- появляется синий шар.

Все эти исходы образуют полную группу попарно несовместимых событий.

Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующим этому событию.

В нашем примере благоприятствующими событию А следующие 5 исходов:

Т.е., событие А наблюдается, если наступает один из исходов, благоприятствующих А: в нашем примере , или, или, или, или.

В этом смысле событие А подразделяется на несколько элементарных событий (), элементарное событие не подразделяется на другие события.

Отношение числа благоприятствующих событию А элементарных исходов к их общему числу называют вероятностью события А и обозначают Р(А).

В примере: всего элементарных исходов 6, из них 5 благоприятствующие событию А Р(А)=.

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Р(А)=,

где m – число элементарных исходов, благоприятствующих А;

n – число всех возможных элементарных исходов испытания.

Здесь предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу.

Свойства из определения вероятности:

Свойство 1. Вероятность достоверного события равна единице:

Р(А)=

Действительно, если событие достоверное, то каждый элементарный исход испытания благоприятствует событию

m = n

Свойство 2. Вероятность невозможного события равна нулю.

Р(А)= .

Действительно, если событие невозможно, то один из элементарных исходов испытания не благоприятствует событию.

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания

, т.е. 0 < P(A) < 1

вероятность любого события:

Статическая вероятность

Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно.

Часто невозможно представить результат испытаний в виде совокупности элементарных событий.

Трудно указать основания, позволяющие считать элементарные события равновозможными.

Поэтому используют другие определения:

Статическое определение вероятности: в качестве статической вероятности, события принимают относительную частоту или число, близкое к ней.

Для существования статической вероятности события А требуется:

Возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие А или наступает или не наступает;

устойчивость относительных частот появления А в различных сериях достаточно большого числа испытаний.

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 2

АКСИОМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ, СЛЕДСТВИЯ ИЗ АКСИОМ. ГЕОМЕТРИЧЕСКАЯ ВЕРОЯТНОСТЬ.

Пусть в результате испытания наступает одно и только одно из событий

События называютэлементарными событиями (элементарными исходами).

Уже отсюда следует, что элементарные события попарно несовместимы.

Множество всех элементарных событий, которые могут появиться в испытаниях, называют пространством элементарных событий , а сами элементарные события – точками пространства .

Событие А отождествляют с подмножеством (пространства ), элементы которого есть элементарные исходы, благоприятствующие.

Множество всех событий, которые могут наступить в испытании, есть множество всех подмножеств .

- достоверное событие; пустое подмножество пространства - невозможное событие.

Каждому элементарному исходу ставят в соответствие число р_i – вероятность этого исхода, причем .

По определению, вероятность Р(А) события равна сумме вероятностей элементарных исходов, благоприятствующих А.

Поэтому вероятность достоверного события равна единице, невозможного – нулю, произвольного – заключена между нулем и единицей.

Построение логически полноценной теории вероятностей основано на аксиоматическом определении случайного события и его вероятности.

В системе аксиом, предложенной А, Н. Колмогоровым, неопределяемыми понятиями являются элементарное событие и вероятность.

Аксиомы определяющие вероятность:

Каждому событию А поставлено в соответствие неотрицательное действительное число Р(А). Это число называется вероятностью события А.

Вероятность достоверного события равна единице.

Вероятность наступления хотя бы одного из попрано несовместимых событий равна сумме вероятностей этих событий.

Геометрические вероятности

Классическое определение вероятности неприменимо к испытаниям с бесконечным числом исходов, поэтому вводится геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.).

Пусть отрезок l составляет часть отрезка L.

На отрезокL наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка к длине отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством

Пример 1. На отрезке ОА длинны L числовой оси ОХ наудачу поставлена точка В(Х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеют длину, большую .

Решение:

ОС=CD=DA=

Т

D

ребование задачи будет выполнено, если

Пример 2.Пусть плоская фигура g составляет часть плоской фигуры G. На G брошена наудачу точка. Вероятность попадания точки в область g равна

Пример. Две концентрические окружности R=10, r=5. Найти вероятность того, что брошенная наудачу в большой круг точка, попадет в кольцо.

Р

ешение. Площадь кольца

Замечание 1. Приведенные определения являются частными случаями общего определения геометрической вероятности. Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки, брошенной наудачу в область g – часть области G,

Замечание 2. В случае классического определения вероятность достоверного события равна 1, невозможно равенство 0, верны обратные утверждения, т.е. если вероятность равна 1, то событие достоверное, если вероятность события равна 0, то событие невозможно.

В геометрическом определении вероятности обратные утверждения не имеют места.

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 3

ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ. ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ НЕСОВМЕСТИМЫХ СОБЫТИЙ.

Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий.

Пример. Из орудия произвели два выстрела. Событие А – попадание при первом выстреле, В – попадание при втором выстреле. А+В – попадание при первом выстреле или попадание при втором выстреле, или в обоих выстрелах.

Если А и В несовместимые события, то А+В – событие состоящее в появлении одного из этих событий.

Суммой нескольких событий называют событии, которое состоит в появлении хотя бы одного из этих событий.

Теорема сложения несовместимых событий.

Вероятность появления одного из двух несовместимых событий, безразлично какого, равна сумме вероятностей этих событий: P(A+B)=P(A)+P(B).

Доказательство: пусть n – общее число возможных элементарных исходов испытания, m₁ – число исходов, благоприятствующих событию А, m₂ – число исходов, благоприятствующих событию В.

Число элементарных исходов благоприятствующих событию А, либо событию В, равно m₁+m₂, значит

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Доказательство проводиться методом индукции.

Пример 1. В урне 30 шаров: 10 – красных, 5 – синих, 15 – белых. Найти вероятность появления цветного шара.

Вероятность появления красного:

Вероятность появления синего:

События А и В несовместны, поэтому можно применить теорему сложения

Полная группа событий

Теорема. Сумма вероятностей событий , образующих полную группу равна единице:

Доказательство: т.к. события - это достоверные события, то. Любые два события полной группы несовместны, значит можно применить теорему сложения. ч.т.д.

Противоположные события

Противоположными называют два единственно возможных события, образующих полную группу. Обозначение:

Пример. 1) Попадание и промах при выстреле по цели – противоположные события

2) При бросании монеты: выпадение герба или надписи – противоположные события.

Теорема. Сумма вероятностей противоположных событий равна единице:

Доказательство: Противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице.

Замечание. При решении задач на нахождение вероятности события А часто выгодно сначала вычислить вероятность события , а затем найти вероятность по формуле

Теорема сложения вероятностей совместных событий.

Два события называют совместными, если появление одного из них не исключает появления другого в одном и том же событии.

Пример 1: А – появление четырех очков при бросании игральной кости, В – появление четного числа очков. События А и В совместные.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Доказательство: Т.к. А и В по условию совместны, то событие А+В наступит, если наступит одно из следующих трех несовместных событий

По теореме сложения несовместных событий: (**)Событие А произойдет, если наступит одно из двух несовместных событий:По теореме сложения несовместных событий:

Аналогично,

Подставим получимч.т.д.

Замечание 1: При использовании полученной формулы следует иметь в виду, что события А и В могут быть как зависимыми, так и независимыми:

для независимых событий:

для зависимых событий:

Замечание 2: Если А и В несовместные события, то их совмещение есть невозможное событие, т.е.

Пример: Вероятность попадания в цель при стрельбе первого и второго орудий соответственно равны Найти вероятность попадания в цель при одном залпе (из обоих орудий) хотя бы одним из орудий.

Решение:

1 сл. Событие А – попадание из 1-го орудия, В – попадание из 2-го орудия, независимы.

Вероятность события AB (оба орудия дали попадание)

Искомая

2 сл. Т.к. А, В независимы, то

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 4

УСЛОВНАЯ ВЕРОЯТНОСТЬ. ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ ДЛЯ ЗАВИСИМЫХ И НЕЗАВИСИМЫХ СОБЫТИЙ.

Принцип практической невозможности маловероятных событий.

При решении многих практических задач приходится иметь дело с событиями, вероятность которых близка к нулю. Можно ли считать, что маловероятное событие А в единичном испытании не произойдет? Такого заключения сделать нельзя т.к. не исключено, хотя и мало вероятно, что событие А наступит. Однако длительный опыт показывает, что маловероятное событие в единичном испытании в подавляющем большинстве случаев не наступает.

Принцип практической невозможности маловероятных событий.

Если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании это событие не наступит. Возникает вопрос? Насколько малой должна быть вероятность, чтобы можно было считать невозможным появление этого события в одном испытании? Ответить однозначно на этот вопрос нельзя. В разных задачах считают по-разному.

Пример. 1) Если вероятность того, что парашют при прыжке не раскроется, равна 0.01, то было бы недопустимым применять такие парашюты.

2) Если же считать, что вероятность того, что поезд дальнего следования прибудет с опозданием, равным 0.01, то можно практически быть уверенным, что поезд прибудет вовремя.

Достаточно малую вероятность, при которой (в данной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике обычно принимают уровни значимости, заключенные между 0.01 и 0.05. Аналогично для событий: .

Следствие. Если случайное событие имеет вероятность, очень близкую к единице, то практически можно считать, что в единичном испытании, что событие наступит.

Теорема умножения вероятностей.

Произведением двух событий А и В называют событие АВ, состоящие в совместном появлении (совмещении) этих событий.

Пример. А – деталь годная;

В – деталь окрашена,

то АВ деталь годная и окрашенная.

Произведением нескольких событий называют события, состоящее в совместном появлении этих событий.

Пример. А, В, С – выпадение герба в 1-ом, 2-ом, и 3-ем случаях, то АВС – появление герба во всех 3-х случаях.

Условная вероятность.

Если при вычислении вероятности события никаких других ограничений, кроме условий S не налагается, то такую вероятность называют безусловной, если же налагаются и другие дополнительные условия, то вероятность события называют условной.

Часто вычисляют вероятность события В при дополнительном условии, что производило событие А.

Условной вероятностью называют вероятностью события В, вычисленную в предположении, что событие А уже наступило.

Условная вероятность события В при условии, что событие А уже наступило, по определению, равна

Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимали по одному шару, не возвращая обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая вероятность условная:

Этот же результат можно получить по формуле (Проверить самостоятельно).

Теорема умножения

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: (*)

Доказательство. По определению условной вероятности

Отсюда, .

Замечание. Применив формулу (*) к событию ВА, получим

Но т.к. АВ не отличается от события ВА, то

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились: , где- вероятность события, вычисленная в предположении, что событиянаступили. В частности, для трех событий:

Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый валик – конусный, а второй – эллиптический.

Решение. Вероятность того, что первый валик окажется конусным (событие А); . Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик – конусный, т.е. условная вероятность. По теореме умножения, искомая вероятность, заметим, что сохранив обозначения легко найдем:.

Пример 2. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что извлекают один шар наудачу, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А), при втором – черный (событие В) и при третьем – синий (событие С).

Решение. Вероятность появления белого шара в первом испытании .

Вероятность появления черного шара во втором испытании в предположении, что в первом испытании появился белый, т.е. условная вероятность .

Вероятность появления синего шара в третьем испытании вычислен, в предположении, что в первом испытании появился белый шар, а во втором – черный, т.е. условная вероятность: .

Искомая вероятность .

Независимые события. теорема умножения для независимых событий.

Пусть вероятность события В не зависит от появления события А.

Событие В называют независимым от события А, если появление события А не изменяет вероятности появления В, т.е. если условная вероятность события В равна его безусловной вероятности: , тогда.

Если событие А не зависит от события В, то и событие А не зависит от события В, это означает, что свойство независимости событий взаимно.

И тогда теорема умножения для независимых событий имеет вид

Т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий, в противном случае события называют зависимыми.

Пример. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) 0.8, а вторым (событие В) – 0.7.

Решение. События А и В независимые, по теореме умножения:

Замечание 1. Если события А и В независимы, то независимы также события действительно,Следовательно,

Независимость событий следует и независимость.

Несколько событий называют попарно независимыми, если каждые два из них независимы. Т.е. А, В, С – независимы, если независимы А и В, В и С, А и С.

Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимо каждое событие и все возможные произведения остальных.

Если несколько событий независимы попарно, то отсюда не следует их независимость в совокупности. Т.е. требование независимости в совокупности сильнее требования независимости попарно.

Пример. Пусть в урне 4 шара: 1 – красный (А), 1 – синий (В), 1 – черный (С), 1 – во все три цвета (АВС). Чему равна вероятность того, что извлеченный шар имеет красный цвет.

Решение. Т.к. из четырех шаров два имеют красный цвет, то . Аналогично,

Допустим теперь, что событие В произошло, т.е. взятый шар имеет синий цвет. Из двух шаров, имеющих синий цвет, один шар имеет и красный цвет, поэтому вероятность события А по-прежнему

Другими словами, условная вероятность события А, вычисленная в предположении, что наступило событие В, равна его безусловной вероятности. Следовательно, события А и В независимы. Аналогично придем к выводу, что события А и С, В и С независимы.

Итак, события А, В, С попарно независимы. Независимы ли эти события в совокупности? Оказывается нет. Действительно, пусть извлеченный шар имеет два цвета, например синий и черный. Чему равна вероятность того, что этот шар имеет и красный цвет? Лишь один шар окрашен во все три цвета, поэтому взятый шар имеет и красный цвет. Таким образом, допустив, что события В и С произошли, приходим к выводу, что событие А обязательно наступит. Т.е. .

Итак, попарно независимые события А, В и С не являются независимыми в совокупности.

Следствие. (из теоремы умножения)

Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Доказательство. Рассмотрим три события А, В и С равносильно совмещению событий АВ и С, поэтому . Т.к. события А, В и С независимы в совокупности, то независимы, в частности, события АВ и С, а также А и В. По теореме умножения для двух независимых событий имеем:Итак, окончательно получим, для произвольногоn доказательство проводиться методом математических индукций.

Замечание. Если события независимы в совокупности, то и противоположны им событиятакже независимы в совокупности.

Пример 2. Найти вероятность совместного появления герба при одном бросании двух монет.

Решение. Вероятность появления герба первой монеты (событие А) . Вероятность появления герба второй монеты (событие В)

События А и В независимые, поэтому искомая вероятность по теореме умножения равна .

Пример 3. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Решение. Вероятность того, что их первого ящика вынута стандартная деталь (событие А),

Вероятность того, что из второго ящика вынута стандартная деталь (событие В)

Вероятность тог, что из 3-го ящика вынута стандартная деталь (событие С)

Т.к. события А, В и С независимые в совокупности, то искомая вероятность (по теореме умножения)

Пример 4. Вероятности появления каждого из трех независимых событий соответственно равны. Найти вероятность появления только одного из этих событий.

Решение. Появление только первого события А, равносильно появлению события (появится первое, но не появится второе и третье)

Обозначим

- появится только ,

- появится только ,

- появится только ,

Т.е. искомая вероятность

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 5

ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ВЕРОЯТНОСТЬ ГИПОТЕЗ. ФОРМУЛЫ БЕЙЕСА.

Формула полной вероятности

Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Доказательство: По условию, событие А может наступить, если наступит одно из несовместных событий Другими словами, появление события одного (безразлично какого), из событий

По теореме сложение:

по теореме умножения зависимых событий, имеем:

Подставив полученные соотношения в равенство (*) имеем:

ч.т.д.

Пример 1: Имеется два набора деталей. Вероятность того, что деталь первого набора стандартная, равна 0.8, а второго – 0.9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная.

Решение:

А – извлеченная деталь стандартная;

–деталь извлечена из 1-го набора;

–деталь извлечена из 2-го набора.

Условная вероятность того, что из первого набора будет извлечена стандартная деталь

По формуле полной вероятности

Пример 2: В первой коробке 20 радиоламп, из них 18 – стандартных, во второй: 10 – из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую коробку. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартная.

Решение:

А – из первой коробки извлечена стандартная лампа;

–из второй коробки извлечена стандартная лампа;

–из второй коробки извлечена нестандартная.

Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй будет переложена стандартная лампа

Условная вероятность того, что из первой коробки будет извлечена стандартная, при условии, что из второй будет переложена нестандартная

По формуле полной вероятности, искомая вероятность того, что из 1-ой коробки будет извлечена стандартная

Вероятность гипотез. Формулы Бейеса.

Пусть событие А может наступить при условии появления одного из несовместных событий образующих полную группу. Т.к. заранее неизвестно, какое из этих событий наступит, их называютгипотезами.

Вероятность события А определяется по формуле полной вероятности:

Допустим, произведено испытание, в результате которого появилось событие А. Определим, как изменились (в связи с тем, что событие А наступило) вероятности гипотез. Т.е. найдем вероятности событий:

Найдем по теореме умножения

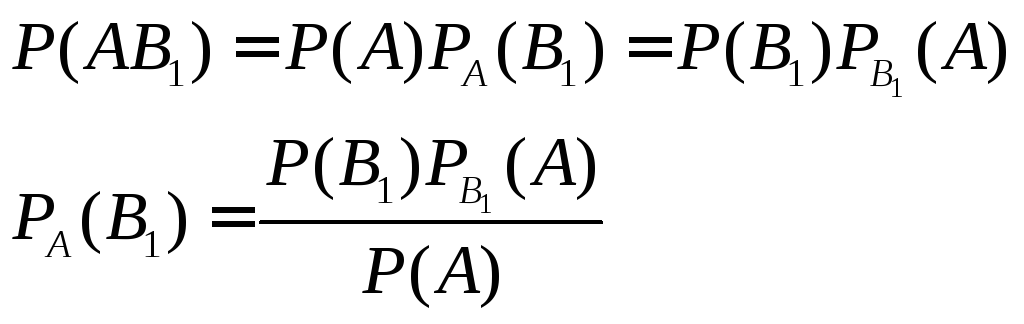
Подставим P(A) из формулы (*), получим:

Аналогично выводятся формулы, определяются условные вероятности остальных гипотез. Т.е. условная вероятность любой гипотезы:

Формулы Бейеса (по имени английского математика, который их вывел в 1764 г.)

Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становиться известным результат испытания, в итоге которого появилось событие А.

Пример: Детали попадают для проверки к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру – 0.6, ко второму – 0.4. Вероятность того, что деталь будет признана стандартной первым контролером – 0.94, вторым – 0.98. Годная деталь при проверке признана стандартной. Найти вероятность того, что эту деталь проверит первый контролер.

Решение: А – деталь признана стандартной;

Гипотеза – деталь проверил первый контролер;

– деталь проверил второй контролер.

Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Бейеса:

(вероятность, что деталь попадает к первому контролеру)

(вероятность, что деталь попадает ко второму контролеру)

Искомая вероятность:

До испытания вероятность гипотезы а после испытания вероятность гипотезы

стала равна 0.59.

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 6

ПОВТОРЕНИЕ ИСПЫТАНИЙ. ФОРМУЛА БЕРНУЛЛИ. ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА. ИНТЕГРАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА.

Если производиться несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

Мы будем рассматривать независимые испытания, в которых событие А имеет одну и ту же вероятность.

Сложным событием называют совмещение нескольких отдельных событий, которые называют простыми.

Пусть производиться n независимых испытаний в которых событие А может появиться либо не появиться. Обозначим вероятность события А в каждом испытании через P, тогда вероятность не наступления события А в каждом испытании также постоянна и равна Вычислим вероятность того, что приn испытаниях событие А осуществится ровно k раз, а значит, не осуществится n-k раз. Не требуется, чтобы событие А повторилось ровно k раз в определенной последовательности.

Например, если говорить о появлении события А три раза в четырех испытаниях, то возможны следующие сложные события: Записьозначает, что в первом, втором и третьем испытаниях событие А наступило, а в четвертом не появилось, т.е. наступило противоположное событие

Искомую вероятность обозначим Вероятность сложного события, состоящего в том, что вn испытаниях события А наступит k раз и не наступит n-k раз, по теореме умножения вероятностей независимых событий равна:

Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е.

Т.к. эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Т.к. вероятности всех этих сложных событий одинаковы, то искомая вероятность равна:

или - формула Бернулли

Пример: Вероятность того, что расход электроэнергии в продолжении суток не превысит нормы, равна Найти вероятность того, что в ближайшие 6 суток расход энергии в течение 4 суток не превысит нормы.

Решение: Вероятность нормированного расхода энергии в продолжении которых из 6 суток постоянна и равна Значит, вероятность перерасхода энергии в каждые сутки также постоянна и равна Искомая вероятность по формуле Бернулли равна:

Локальная теорема Лапласа.

Использование формулы Бернулли при больших значениях n приводит к большим вычислениям. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события равное k раз в n испытаниях, если число испытаний достаточно велико.

(Функцию называют асимптотически приближенной функцииесли)

Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится вn испытаниях равно k раз, приближенно равна (тем точнее, чем больше n) значению функции:

Имеются таблицы, в которых помещены значения функции

для положительного значения

Приложение 1. Для отрицательных значений пользуются теми же таблицами, т.к. функция- четная, т.е.

Итак, вероятность того, что событие А появится в n независимых испытаниях равно k раз, приближенно равна:

Пример 1. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0.2.

Решение:

Воспользуемся асимптотической формулой Лапласа:

По формуле Бернулли:

Пример 2. Вероятность поражения мишени стрелком при одном выстреле Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

Решение:

По асимптотической формуле Лапласа:

По формуле Бернулли:

Расхождение объясняется тем, что n имеет малое значение, а формула Лапласа дает достаточно хорошее приближение лишь при больших n.

Интегральная теорема Лапласа.

Пусть производится n испытаний, в каждом из которых вероятность появления события А постоянна и равна Как вычислить вероятностьтого, что событие А появится вn испытании не менее раз, и не болеераз?

Если вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится вn испытаниях от дораз, приближенна равна определенному интегралу

При решении задач используют таблицы интеграла

(приложение 2)

Функция - нечетнаяВ таблице приведены значения лишь дот.к. дляможно лишь принятьназывают функцией Лапласа.

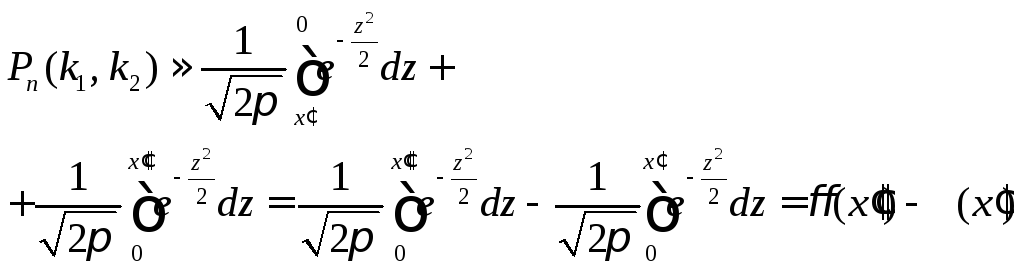
Итак, вероятность того, что событие А появится в n независимых испытаниях от дораз,

Пример. Вероятность того, что деталь не прошла проверку равна Найти вероятность того, что среди 400 случаев отобранных деталей окажется непроверенных от 70 до 100 деталей.

Решение:

Замечание: Обозначим через m число появлений событий А при n независимых испытаниях, в каждом из которых вероятность наступления события А равна p.

Если m изменяется от дото дробьизменяется отдо

Значит,

Вероятность отклонения относительно частоты от постоянной вероятности в независимых испытаниях.

Пусть производная n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна Найдем вероятность того, что отклонение относительной частотыот постоянной вероятностиP по абсолютной величине не превышает заданного . Т.е. найдем вероятность осуществления неравенства

Эту вероятность будем обозначать так:

Преобразуем неравенство (*):

воспользуемся замечанием:

положим:

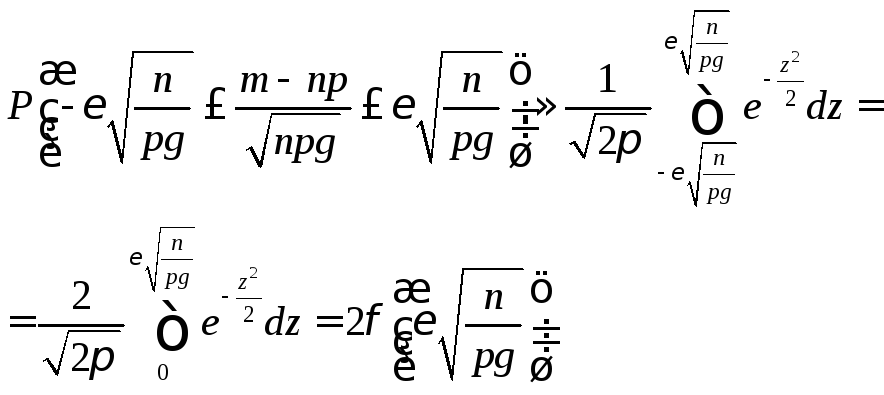
Т.е.

Т.е. вероятность осуществления неравенства

Приближено равна значению удвоенной функции Лапласа

Пример. Вероятность того, что деталь не стандартная, Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности 0.1, по абсолютной величине не более чем на 0.03.

Решение:

По приложению 2

Вывод: если взять достаточно большое число проб по 400 деталей в каждой, то примерно 95.44% этих проб отклонение относительной частоты от постоянной вероятности по абсолютной величине не превысит 0.03.

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 7.

ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. ЗАКОН РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, ДИСПЕРСИЯ И ИХ СВОЙСТВА.

Случайная величина.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Пример:

1) При бросании игральной кости могли появиться числа 1, 2, 3, 4, 5, 6. Наперед определить число очков есть величина случайная; числа 1, 2, 3, 4, 5 и 6 есть возможные значения этой величины.

2) Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующее возможные значения: 0, 1, 2, …, 100.

3) Расстояние, которое пролетит снаряд при выстреле – случайная величина. Возможное значение этой величины .

Обозначение. Случайные величины обозначают X, Y, Z, …, а их возможные значения – соответствующими строчными буквами x, y, z, …

Например, если X – случайная величина имеет три возможных значения, то они будут обозначаться

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. (пример, 1 и 2)

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно. (Замечание. Это определение не является точным, более строгое определение будет дано позднее) (Пример 3)

Закон распределения вероятностей дискретной случайной величины.

Для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности. (т.к. случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их – различные).

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями, его можно задать таблично, аналитически (в виде формулы) и графически.

Таблично:

X			…		возможные значения
P			…		их вероятности

Т.к. в одном испытании случайная величина принимает одно и только одно возможное значение, события образуют полную группу, значит

Если множество значений Х бесконечно (счетно), то ряд сходится и его сумма равна единице.

Пример: В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 рублей и 10 выигрышей по 1 рублю. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.

Решение: Напишем возможные значения Х:

Вероятности этих возможных значений:

Закон распределения:

X	50	1	0
P	0.01	0.1	0.89

Для наглядности закон распределения дискретной случайной величины можно изобразить графически. В прямоугольной системе координат строят точкиа затем соединяют их отрезками.

Полученную фигуру называют многоугольником распределения.

Математическое ожидание дискретной случайной величины.

Закон распределения случайной величины – его полная вероятностная характеристика.

Определение: Числовыми характеристиками случайной величины (закона распределения) называются специальные числа, описывающие отдельные свойства случайной величины.

Различных числовых характеристик существует бесконечное множество.

Мы выделим среди них числовые характеристики положения и рассеяния.

К числовым характеристикам положения в первую очередь относится математическое ожидание.

Определение: Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

(Обозначают )

соответствующие вероятности тогда

если дискретная величина Х принимает счетное множество возможных значений, то

причем математическое ожидание существует, если ряд в правой части равенства сходиться абсолютно

(- конечен и)

Замечание: Математическое ожидание дискретной случайной величины есть неслучайная величина (т.е. постоянная).

Пример 1. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна p.

Х – число появлений А.

X	0	1
		p

Т.е. математическое ожидание числа появлений события в одном испытании равно вероятности.

Вероятностный смысл математического ожидания.

Пусть в n испытаниях случайная величина Х приняла раз значениераза значение…,раза значениетогда сумма всех значений, принятых Х, равнасреднее арифметическоевсех значений

или

- относительная часть значения

- относительная часть значения

- относительная часть значения

При большом числе испытаний

Вероятностный смысл: математическое ожидание приближенно равно (тем точное, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Замечание 1. Т.к. математическое ожидание меньше наибольшего возможного значения и больше наименьшего, то его часто называют центром распределения,

Свойства математического ожидания.

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:

Доказательство: Постоянная С – будем рассматривать как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:

Доказательство: Пусть случайная величина Х задается законом распределения:

X			…
P			…

Произведения постоянной величины С на дискретную случайную величину Х определяется как дискретная величина с возможными значениями равными произведению С на возможное значение Х, с вероятностями равными соответствующим вероятностям Х.

Т.е. закон распределения случайной величины СХ:

			…
P			…

Математическое ожидание случайной величины СХ:

Замечание 2. Две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае случайные величины зависимы.

Несколько случайных величин называют взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.

Замечание 3. Произведение независимых случайных величин Х и Y определяется как случайная величина ХY, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение Y, вероятности возможных значений ХY равны произведениям вероятностей возможных значений.

Некоторые произведения могут оказываться равными между собой, в том случае вероятность возможного значения произведения равна сумме соответствующих вероятностей.

Например, если , то вероятность(или, что то же) равна

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий

Доказательство: Пусть независимые случайные величины Х и У заданы своими законами вероятностей (для простоты возьмем по два возможных значения):

Х
P

У
P

Тогда

ХУ
P

Следствие: Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.

Замечание: Определим сумму случайных величин Х и У как случайную величину возможные значения которой равны суммам каждого возможного значения у; вероятности возможных значенийдля независимых Х и У равны произведениям слагаемых, для зависимых величин – произведениям вероятности одного слагаемого на условную вероятность второго.

Если некоторые суммы могут оказаться равными, тогда вероятность возможного значения суммы равна сумме соответствующих вероятностей.

Например, если а соответственно вероятности равны, то вероятность(или, что тоже,) равна

Свойство 4. Математическое ожидание суммы двух случайных величин (и зависимых и не зависимых) равно сумме математических ожиданий слагаемых:

Доказательство: Пусть

Х
P

У
g

Тогда

P

Тогда

т.к. событие состоящее в том, что Х примет значение влечет за собой событие, которое состоит в том, чтопримет значениеилии обратно.

Аналогично

Получаем

Следствие: Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.

Пример: Производится 3 выстрела с вероятностями попадания в цель Найти математическое ожидание общего числа попаданий.

Решение: Число попаданий при первом выстреле есть случайная величина , которая может принимать только два значения: 1 (попадание) с вероятностьюи 0 (промах) с вероятностью

Аналогично, - математическое ожидание числа попаданий при втором вы стреле;

- математическое ожидание числа попаданий при третьем выстреле.

Общее число попаданий есть случайная величина, состоящая из суммы попаданий в каждом из трех выстрелов:

Математическое ожидание числа появлений события в независимых испытаниях.

Пусть производиться n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна p.

Математическое ожидание числа появлений события А вn независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:

или математическое ожидание биноминального распределения с параметрами n и p равно

Дисперсия дискретной случайной величины.

Различные случайные величины могут иметь одно и тоже М. О.

У	-100	100
p	0.5	0.5

Х	-0.01	0.01
P	0.5	0.5

Однако характер распределения дискретных случайных величин Х и У различен, т.к. Х принимает значения близкие М.О., а У – значения весьма отдаленные от М.О. Поэтому вводят и другие числовые характеристики.

Отклонением называют разность между случайной величиной и ее М.О.

Х			…
p			…

Тогда, закон распределения отклонения

			…
p			…

Математическое ожидание отклонения равно 0.

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Х			…
p			…

Тогда квадрат отклонения имеет следующий закон распределения:

				…
p				…

Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадрата ее математического ожидания

Доказательство: т.к. - постоянная величина, то- тоже постоянные величины.

Воспользовавшись свойствами математического ожидания:

Свойства дисперсии.

1) Дисперсия постоянной величины С равно 0.

Доказательство:

2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

Доказательство:

3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

Доказательство: По формуле для всех D:

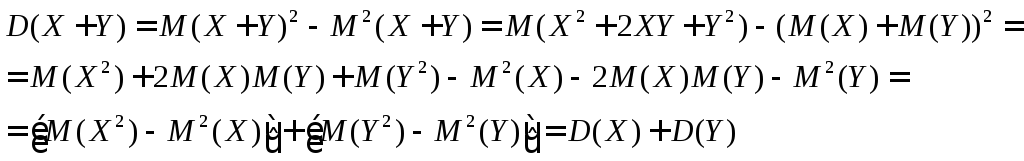Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.

Следствие 2.

4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

Доказательство:

Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность p появление событий постоянна, равна произведению числа испытаний на вероятности появления и не появления события в одном испытании:

или

Дисперсия биноминального распределения с параметрами n и p равна произведению npg.

Среднее квадратическое отклонение.

Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии:

Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

Доказательство: Пусть тогда по следствию из свойства дисперсии суммы:

Одинаково распределенные взаимно независимые случайные величины.

Рассмотрим n взаимно независимых случайных величин которые имеют одинаковые распределения, а значит, и одинаковые характеристики.

Обозначим среднее арифметическое рассматриваемых случайных величин через :

1) Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию a каждой из величин:

Доказательство:

2) Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин:

Доказательство:

3) Среднее квадратическое отклонение среднего арифметического n одинаково распределенных независимых случайных величин в раз меньше среднего квадратического отклонениякаждой из величин:

Доказательство: т.к.

Вывод из 2) и 3): среднее арифметическое достаточно большого числа взаимно независимых случайных величин имеет значительно меньшее рассеяние, чем каждая отдельная величина.

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 8

НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ И ЕЕ СВОЙСТВА.

Функция распределения вероятностей случайной величины.

Пусть x – действительное число. Х – случайная величина.

Вероятность события состоящего в том, что Х примет значение, меньшее x, т.е. обозначим

Функцией распределения называют , определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшееx, т.е.

Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Напоминание.

1. Функция непрерывна в промежутке Х, если она непрерывна в каждой точке промежутка в отдельности. Функция непрерывна в точке если

2. Если имеет место равенство , где

А -

- бесконечно малая высшего порядка,

То функция называется дифференцируемой, а А – дифференциалом.

Свойства функции распределения.

1) Значения функции распределения принадлежат отрезку :

.

Доказательство: т.к. функция распределения – вероятность.

2) - неубывающая функция, т.е.

Доказательство: пусть . Событие, состоящее в том, что Х примет значение, меньшееможно подразделить на следующие два несовместимых события:

а) Х примет значение меньшее с вероятностью

б) Х примет значение, удовлетворяющее неравенству с вероятностью

По теореме сложения:

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале:

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равно 0.

3) Если возможные значения случайной величины принадлежат интервалу (a, b), то:

а)

Доказательство: а) Пусть Тогда событиеневозможно, и вероятность равна 0.

б) Пусть Тогда событиедостоверно, и вероятность равна 1.

Следствие. Если возможные значения неопределенной случайной величины расположены на всей оси x, то справедливы следующие предельные соотношения:

График функции распределения.

Из доказанных свойств следует:

1. График функции распределения расположен в полосе, ограниченной прямыми

2. При возрастании x в интервале (a, b), график поднимается вверх.

3. При ординаты графика равны 0, приординаты графика равны 1.

Замечание. График функции распределения дискретной случайной величины имеет ступенчатый вид.

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 9

ВЕРОЯТНОСТЬ ПОПАДАНИЯ НА ЗАДАННЫЙ ИНТЕРВАЛ. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ И ЕЕ СВОЙСТВА. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.

Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию - первую производную от функции распределения:

Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.

Вероятность попадания непрерывной случайной величины в заданный интервал.

Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу равна определенному интегралу от плотности распределения, взятому в пределах отa и b:

Доказательство: По следствию 1 из свойства 2 функции распределения:

По формуле Ньютона-Лейбница,

Таким образом,

Геометрический смысл теоремы: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу равна площади криволинейной трапеции, ограниченной осью, кривой распределенияи прямыми

Нахождение функции распределения по известной плотности распределения.

Если - плотность распределения, то функцию распределенияможно найти по формуле:

Доказательство: По определению

По предыдущей теореме:

Таким образом, зная плотность распределения, можно найти функцию распределения, а по известной функции распределения может быть найдена плотность распределения а именно:

Свойства плотности распределения.

1) Плотность распределения – неотрицательная функция:

Доказательство: Функция распределения – неубывающая функция, значит, ее производная - неотрицательная функция.

Геометрически это означает, что точки, принадлежащие графику плотности распределения, расположены либо над осью , либо на этой оси.

График распределения называют кривой распределения.

2) Несобственный интеграл от плотности распределения в пределах равен единице.

Доказательство: Несобственный интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу. Очевидно, такое событие достоверно, следовательно, вероятность его равна единице.

Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью и кривой распределения, равна единице.

Если все возможные значения случайной величины принадлежат интервалу то

Вероятностный смысл плотности распределения.

Пусть - функция распределения непрерывной случайной величины Х. По определению плотности распределения:, или

Разность определяет вероятность того, что Х примет значение, принадлежащее интервалу

Таким образом, предел отношения вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу к длине этого интервала (при) равен значению плотности распределения в точкеx.

По аналогии с определением плотности массы в точке, значение функции в точкеx рассматривают как плотность вероятности в этой точке.

Если масса непрерывно распределена вдоль оси x по некоторому закону, например , то плотность массы в точке x называют предел отношения массы интервала к длине интервала при, т.е.

Из дифференциального начисления известно, что приращение функции приближенно равно дифференциалу функции, т.е.

или

Вероятностный смысл этого равенства:

Вероятность того, что случайная величина примет значение, принадлежащее интервалу приближенно равна (с точностью до бесконечно малых высшего порядка относительно) произведению плоскости вероятности в точкеx на длину интервала .

Геометрически:

Вероятность того, что случайная величина Х примет значение, принадлежащее интервалуприближенно равна площади прямоугольника с основаниеми высотой.

Допустимая при этом погрешность равна площади криволинейного .

Числовые характеристики непрерывных случайных величин.

Пусть непрерывная случайная величина Х задана плотностью распределения .- отрезок, которому принадлежат все возможные значения случайной величины Х.

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку , называют определенный интеграл

Если возможные значения Х принадлежат всей оси , то

Предполагается, что несобственный интеграл сходится абсолютно, т.е. существует интеграл

Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к , а верхнего к.

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения Х принадлежат отрезку , то

Если возможные значения Х принадлежат всей оси , то

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

Замечание 1. Свойства математического ожидания и дисперсии дискретной случайной величины сохраняются и для непрерывных величин.

Замечание 2. Для вычисления дисперсии используют формулы:

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 10

ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ.

Напоминание. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.

Биномиальное распределение (дискретное распределение).

Х			…		…	0
p			…		…

Биномиальное распределение определяется формулой Бернулли:

n – натуральное число,

Числа - называют биномиальными коэффициентами, т.к. они являются коэффициентами разложения бинома Ньютона

Распределение Пуассона (дискретное распределение).

Это закон распределения вероятности массовых (n - велико) и редких (p - мало) событий.

Закон распределения определяется формулой

Случайная величина, распределенная по закону Пуассона, принимает счетное множество значений.

Закон равномерного распределения вероятностей.

Плотности распределения непрерывных случайных величин называют также законами распределения.

Часто встречаются законы нормального, равномерного и показательного распределения.

Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения, случайной величины, плотность распределения сохраняет постоянное значение.

Пример. Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину Х, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними делениями. Таким образом, Х имеет равномерное распределение.

Найдем плотность равномерного распределения , считая, что все возможные значения случайной величины заключены в интервале, на котором функциясохраняет постоянные значения:

По условию Х не принимает значений вне интервала , поэтомупри

Найдем постоянную С. Т.к. все возможные значения Х принадлежат интервалу , то

Отсюда

Итак, искомая плотность вероятности равномерного распределения

График плотности равномерного распределения:

Замечание. Обозначим черезR непрерывную случайную величину, распределенную равномерно на интервале , а черезr – ее возможные значения.

Вероятность попадания R (в результате испытания) в интервале , принадлежащий интервалу, равна его длине:

Действительно, плотность рассматриваемого равномерного распределения

следовательно, вероятность попадания случайной величины R в интервал

Далее случайная величина R часто используется.

Простейший поток событий.

Потоком событий называют последовательность событий, которые наступают в случайные моменты времени.

Примеры потоков: поступление вызовов на АТС, прибытие самолетов в аэропорт, и др.

Выделим свойства потоков:

стационарность;

отсутствие последствия;

ординарность.

Свойство стационарности характеризуется тем, что вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися. Например, вероятности появления k событий на промежутках времени одинаковой длительностиединиц времени равны между собой. Итак, если поток обладает свойством стационарности, то вероятность появленияk событий за промежуток времени длительности t есть функция, зависящая только от k и t.

Свойство отсутствия последствия характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появились или не появились события в моменты времени, предшествующие началу рассматриваемого промежутка. Итак, если поток обладает свойством отсутствия последствия, то имеет место взаимная независимость появлений того или иного числа событий в непересекающееся промежутки времени.

Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно. Т.е вероятность появления одного события пренебрежимо мала по сравнению с вероятностью появления только одного события. Итак, если поток обладает свойством ординарности, то за бесконечно малый промежуток времени может появиться не более одного события.

Простейшим (пуассоновским) называют поток событий, который обладает свойствами стационарности, отсутствия последствия и ординарности.

Замечание: Если поток представляет собой сумму очень большого числа независимых стационарных потоков, влияние каждого из которых на всю сумму (суммарный поток) ничтожно мало, то суммарный поток (при условии его ординарности) близок к простейшему.

Интенсивностью потока называют среднее число событий которые появляются в единицу времени.

Если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за время длительностью t определяется формулой Пуассона:

Эта формула отражает все свойства простейшего потока:

1. Вероятность появления k событий за время t, при заданной интенсивности является функцией k и t, что характеризует свойство стационарности:

2. Формула не использует информации о появлении событий до начала рассматриваемого промежутка, что характеризует свойство отсутствия последствия.

3. Пусть - вероятность не появления события

- вероятность появления одного события

Тогда вероятность появления более одного события

пользуясь разложением

, после преобразований получим

сравнивая иполучаем, при малыхt вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события, что характеризует свойство ординарности.

Итак, формула Пуассона – математическая модель простейшего потока событий.

Пример: Среднее число вызовов, поступающих на АТС в одну минуту, равно 2. Найти вероятность того, что за 5 минут поступит: а) 2 вызова: б) менее 2-х вызовов: в) не менее 2-х вызовов. Поток вызовов предполагается простейшим.

Решение:

Воспользуемся формулой Пуассона:

а) - событие практически невозможно:

б) - невозможно:

в) - практически достоверно.

Геометрическое распределение.

Пусть производиться независимые испытания, в каждом из которых вероятность появления события А равна следовательно, вероятность его не появленияИспытания заканчиваются, как только появиться событие А. Таким образом, если событие А появилось наk-м испытании, то в предшествующих испытаниях оно не появилось.

Обозначим через Х дискретную случайную величину – число испытаний, которые нужно провести до первого появления события А.

Возможными значениями т.е. натуральные числа.

Пусть в первых испытаниях событие А не наступило, а вk-м испытании появилось.

Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий,

Полная в формуле (*), получим геометрическую прогрессию с первым членомp и знаменателем

По этой причине распределение (*) называют геометрическим.

(Самостоятельно) Ряд (**) сходиться и сумма его равна 1.

Пример: Из орудия производиться стрельба по цели до первого попадания. Вероятность попадания в цель Найти вероятность того, что попадание произойдет при третьем выстреле.

Решение:

Гипергеометрическое распределение.

Пусть в партии из N изделий имеется M стандартных

Из партии случайно отбирают n изделий (каждое изделие может быть извлечено с одинаковой вероятностью)

Х – число m стандартных изделий среди n отобранных;

Возможные значения тип (n, M)

Тогда вероятность того, что т.е. среди отобранных изделий ровноm стандартных:

Эта формула определяет распределение вероятностей, которое называют гипергеометрической.

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 11

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. ВЕРОЯТНОСТЬ ПОПАДАНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ, РАСПРЕДЕЛЕННОЙ ПО НОРМАЛЬНОМУ ЗАКОНУ НА ЗАДАННЫЙ ИНТЕРВАЛ. ПРАВИЛО .

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

Выясним вероятностный смысл параметров .

1) Докажем, что

По определению

Введем замену

Новые пределы интегрирования равны старым.

- интеграл Пуассона.

- т.к. нечетная функция, а пределы интегрирования симметричны.

Математическое ожидание нормального распределения равно параметру a.

2) Докажем, что параметр - среднее квадратическое отклонение нормального распределения.

По определению

Введем,

Новые пределы интегрирования равны старым

Среднее квадратическое отклонение нормального распределения равно параметру .

Замечание 1. Общим называют нормальное распределение с произвольными параметрами

Нормированным называют нормальное распределение с параметрами

Если Х – нормальная величина с параметрами , то- нормированная нормальная величина,

Плотность нормированного распределения

(приложение 1)

Замечание 2. Функция - общего нормального распределения

А функция нормированного распределения

Замечание 3. Вероятность попадания нормированной нормальной величины Х в интервал можно найти, пользуясь функцией Лапласа.

Замечание 4. Т.к.

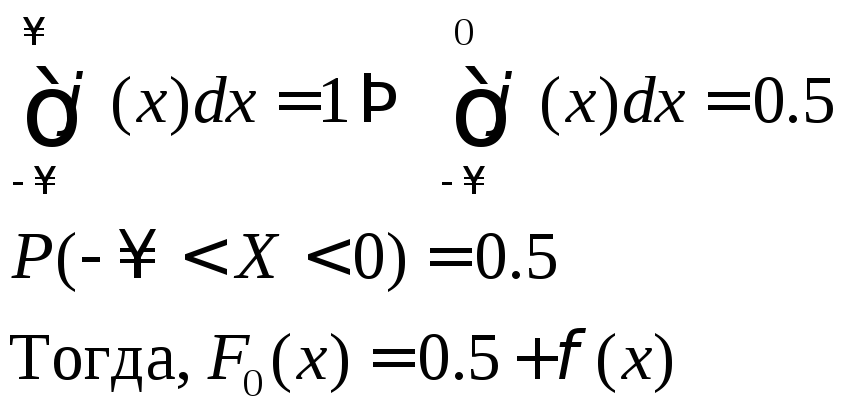
Нормальная кривая.

График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

Исследуем функцию

1. Функция определена на всей оси x.

2. При всех значениях x функция принимает положительные значения, т.е. нормальная кривая расположена над осью .

3. 

4. Исследуем на экстремум

Значит, при функция имеет максимум равный

5. Т.к. - в выражении функции, то график функции симметричен относительно прямой.

6. Исследуем функцию на точки перегиба.

При вторая производная равна 0. А функция в этих точках равнат.е. точки- точки перегиба.

Нормальная кривая при

Влияние параметров нормального распределения на форму нормальной кривой.

Изменение величины параметра (математического ожидания) не изменяет формы кривой, а приводит лишь к ее сдвигу вдоль оси: вправо, есливозрастает; влево, еслиубывает.

Свозрастаниеммаксимальная ордината нормальной кривой убывает, а сама кривая становится более пологой; т.е. сжимается к оси; при убываниинормальная кривая становится более «островершинной» и растягивается в положительном направлении оси.

При любых значениях параметров площадь, ограниченная нормальной кривой и осьюx, остается равной 1 (из свойства плотности распределения).

При нормальную кривую называют нормированной

Вероятность попадания в заданный интервал нормальной случайной величины.

Х – случайная величина, - плотность распределения. Тогда вероятность того, что Х примет значение, принадлежащее интервалу, такова:

Если Х распределена по нормальному закону, то

После преобразований можно получить формулу более удобную для применения

Вычисление вероятности заданного отклонения.

Часто требуется вычислить вероятность того, что отклонение нормального распределения случайной величины Х по абсолютной величине меньше заданного положительного числа т.е. требуется найти вероятность осуществления неравенства

Пользуясь формулой (*):

Замечание. Если две случайные величины нормально распределены и, то вероятность принять значение, принадлежащее интервалубольше у той величины, которая имеет меньшее значение.

Правило трех сигм ()

Преобразуем формулу

положим :

Т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0.9979.

Вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение очень мала, а именно равна 0.0027. Это значит, что лишь в 0.27% случаев так может произойти. Такое событие можно считать практически невозможным.

Правило : если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

На практике: если распределение изучаемой случайной величины неизвестно, то условие, указанное в правиле , выполняется то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

Рекомендуемая литература

1. Высшая математика для экономистов: Учебник для вузов / Под редакцией Н.Ш. Крамера.- М.: Банки и биржи, ЮНИТИ, 1998.

2. Красс М.С. Математика для экономических специальностей: Учебник. – М.: Инфа-М, 1998.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Наука, 2003.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. – М.: Высшая школа, 2003.

Лекция 12

МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ.

Величины, возможные значения которых определяются двумя, тремя и т.д. числами называют двумерными, трехмерными и т.д.

Двумерную случайную величину обозначают . Каждую из величин Х иY называют составляющей (компонентной). Обе величины Х и Y, рассматриваемые одновременно, образуют систему двух величин.

Аналогично n- мерную величину можно рассматривать как систему n случайных величин.

Пример: Станок штампует стальные плитки. Если размерами являются Х длина и ширина Y, то имеет двухмерную случайную величину .

Двухмерную случайную величину можно истолковать как случайную точку на плоскости, либо как случайный вектор.

Различают дискретные (составляющие этих величин дискретны) и непрерывные (составляющие этих величин непрерывны) многомерные случайные величины.

Закон распределения вероятности дискретной двумерной случайной величины.

Законом распределения двумерной случайной величины называют перечень возможных значений этой величины, т.е. пар чисел и их вероятностей

			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…

Т.к. события () () образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы, равна 1.

Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющей: события - несовместимы, поэтому вероятностьтого, что Х примет значение, по теореме сложения такова:

Т.е. вероятность того, что Х примет значение , равна сумме вероятностей «столбца».

Аналогично, чтобы найти надо сложит вероятности столбца.

Сложив вероятности строки получим вероятность

Функция распределения двумерной случайной величины.

Функцией распределения двумерной случайной величины называют функцию, определяющую для каждой парывероятность того, что Х примет значение, меньшееx, и при этом примет значение, меньшее:

Геометрически: это бесконечный квадрат с вершиной , расположенный левее и ниже этой вершины.

Свойства функции распределения.

1)

2) - неубывающая функция по каждому аргументу, т.е.

3) Имеют место предельные соотношения:

а)

б)

в)

г)

4) а) при функция распределения системы становится функцией распределения составляющей Х:

б) при функция распределения системы становится функцией распределения составляющейY:

Вероятность попадания случайной точки в полуполосу.

Полуполоса Полуполоса

Вероятность попадания случайной точки в прямоугольник.

Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности).

Плотностью совместного распределения вероятностей двумерной непрерывной случайной величиныназывают вторую смешанную частною производную от функции распределения:

(Предполагается, что всюду непрерывна и имеет всюду (за исключением, быть может, конечного числа кривых)непрерывную частную производную второго порядка).

Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.

Пример: Найти плотность совместного распределения системы случайных величин, если функция распределения

По определению

Нахождение функции распределения системы по известной плотности распределения.

Вероятность попадания случайной точки в произвольную область.

Свойства двумерной плотности вероятности.

1)

2)

Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен 1.

Отыскание плотностей вероятности составляющих двумерной случайной величины.

Плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, причем переменная интегрирования соответствует другой составляющей.

Условные законы распределения составляющих системы дискретных случайных величин.

Вспомним, если событие А и B зависимы, то условие вероятности события B:

Аналогичное положение имеет место и для случайных величин.

Рассмотрим дискретную двумерную случайную величину пусть возможные значения составляющих таковы:

Допустим, в результате испытания величина Y приняла значение , при этомX принимает одно из возможных значений:

Обозначим условную вероятность того, что X примет, например, значение при условии, что, через

В общем случае:

Условным распределением составляющей X при ,называют совокупность условных вероятностей, вычисленных в предположении, что событие(j имеет одно и то же значение при всех значениях X) уже наступило.

Аналогично определяется условное распределение Y.

Условные законы распределения составляющей X определяется соотношением:

Аналогично находятся условные законы распределения составляющей Y:

Замечание. Суммой вероятностей условного распределения равна 1.

Условные законы распределения составляющих системы непрерывных случайных величин.

Пусть - непрерывная двумерная случайная величина.

Условной плотность распределения составляющейX при данном значении называют отношение плотности совместного распределениясистемык плотности распределениясоставляющейY:

Аналогично,

Формулы для вычисления условной плотности:

Условные плотности облают следующими свойствами:

Условное математическое ожидание.

Условным математическим ожиданием дискретной случайной величины Y при называют произведение возможных значенийY на их условные вероятности:

Для непрерывной случайной величины:

где - условная плотность случайной величиныY при .

Условное математическое ожидание есть функция отx:

которую называют функцией регрессии Y на X.

Аналогично определяются условное математическое ожидание случайной величины X и функции регрессии X на Y:

Математическое ожидание и дисперсия случайного вектора

Математическим ожиданием n-мерного случайного вектора называется вектор, составленный из математических ожиданий координат.

Дисперсией n-мерного случайного вектора называется вектор, составленный из дисперсий координат.

Математическое ожидание и дисперсия координат вычисляются по формулам, которые мы запишем для случая .

Если (X,Y) - дискретный случайный вектор, то

, ,.

, .

Ковариация. Коэффициент корреляции

Важной характеристикой двумерной (n-мерной) является ковариация (матрица ковариации, или дисперсионная матрица).

Ковариацией (корреляционным моментом) случайных величин X и Y называется число, определяемое формулой

(1)

Из определения ковариации и свойства линейности МО следует, что

(2)

Рассмотрим свойства ковариации.

Свойство 1. Если X и Y - независимые случайные величины, то . Следует из (2). Свойство 1 дает достаточный признак зависимости случайных величин X и Y.

Свойство 2. . Следует из определения ковариации и дисперсии.

Свойство 3. .

Свойство 4. cov(с₁X+c₂Y,Z)=с₁сov(X,Z)+с₂cov(Y,Z), где c₁ и с₂ - постоянные. Свойство 4 следует из определения ковариации и свойства линейности МО.

С ковариацией случайных величин X и Y может быть связана матрица

,

которая называется матрицей ковариации. Очевидно, что она симметричная.

Если -n-мерный случайный вектор, то для него также может быть записана матрица ковариации, которая имеет матричные элементы σ_ij, определяемые равенствами

.

Отсюда видно, что ,то есть матрица ковариации симметричная.

Используя ковариацию, можно получить формулу для дисперсии линейной комбинации двух (и нескольких) случайных величин без предположения их независимости.

Утверждение. Если для случайных величин X и Y существует cov(X,Y), то при любых с₁, и с₂ существует

(3)

Действительно,

.

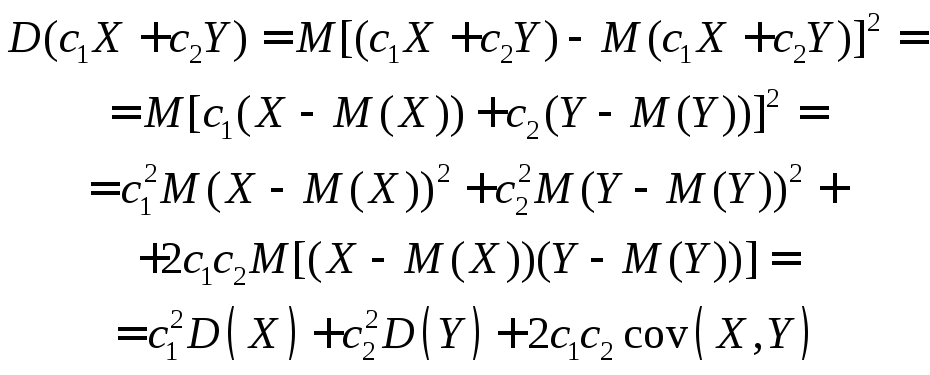Для п-мерного случайного вектора формула (3) принимает вид

Используя свойство неотрицательности дисперсии из формулы (3), положив в ней с₁=t, с₂=1, получим

при любом Отсюда дискриминант

или ,

то есть

. (4)

Выше было отмечено, что для независимых случайных величин X и Y .

Следовательно, если , то случайные величины X и Y зависимы.

В качестве количественной характеристики степени зависимости случайных величин X и Y вводится коэффициент корреляции.

Коэффициентом корреляции случайных величин X и Y называется число, определяемое формулой

(5)

Для ρ_x,y справедливо утверждение:

коэффициент корреляции удовлетворяет неравенству |ρ_x,y|≤1, причем если Y линейно выражается через X, то есть , гдеа и b -постоянные, то .

Первая часть утверждения следует из неравенства (4). Докажем вторую его часть. Пусть . Тогда

Используя (5), получаем

.

Имеет место и обратное утверждение: если коэффициент корреляции |ρ_x,y|=1, то между X и Y существует линейная связь.

Отметим, что из свойства 1 ковариации следует, что для независимых случайных величин X и Y ρ_x,y=0. Обратное утверждение неверно.

Случайные величины X и Y, для которых ρ_x,y=0, называются некоррелированными.

Из вышеизложенного следует, что независимые случайные величины некоррелированны, а некоррелированные случайные величины необязательно независимы.

Пример. Совместное распределение СB X и Y задано таблицей.

Найти .

X Y	-1	0	1
-1	1/8	1/12	7/24
1	5/24	1/6	1/8

;

.

Нормальный закон распределения двумерной случайной величины