
Downloads_1 / 2y_semestr_Lektsia_15
.pdf
1й курс. 2й семестр. Лекция 15 |
1 |
Лекция 15.
Статистическое описание равновесных состояний. Функция распределения. Барометрическая формула. Распределение Больцмана. Принцип детального равновесия. Распределение Максвелла. Экспериментальная проверка распределения Максвелла. Фазовое пространство. Распределение Максвелла-Больцмана. Равновесные флуктуации. Статистическое обоснование второго начала термодинамики. Формула Больцмана для статистической энтропии.
Математическое отступление.
Пусть при каком-то эксперименте было проведено N испытаний, в результате чего был получен ряд значений искомой величины x: {x1, x2, x3, x4, , xN}. Причем некоторые из этих значений могут быть одинаковыми. Составим таблицу (или как говорят, распределение значений).
Значение x |
x1 |
x2 |
|
… |
|
|
x |
k |
Количество одинако- |
N1 |
N2 |
|
… |
|
|
N |
k |
вых значений |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
При этом N = ∑ Ni . |
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
Определим частоту появления величины xi как отношение pi |
= p ( xi ) = |
Ni |
. |
|
|
|||
|
|
ɶ |
ɶ |
|
|
|
|
|
N
N
∑ xi
Среднее значение величины  x
x = i=1
= i=1
N
N |
xi |
k |
Ni |
k |
|
= ∑ |
= ∑ xi |
= ∑ pi xi . |
|||
N |
|
||||
i=1 |
i=1 |
N i=1 |
|||
В случае повторных экспериментов в тех же условиях можно ожидать, что новое значение средней величины будет несильно отличаться от прежнего значения. В предельном случае бесконечного числа испытаний величина
pi |
|
ɶ |
Ni |
|
|
||
= lim p ( xi ) = lim |
|||
|
N →∞ |
N →∞ N |
|
называется вероятностью появления значения xi .
Предположим, что вероятность pi уже известна для данного эксперимента. Тогда можно рассчитывать, что при проведении N испытаний величина xi выпадет Ni=pi N раз.
В некоторых случаях математический анализ условий проведения эксперимента даёт оценку для вероятности появления величины x в виде определённого интеграла
x2
p ( x1 < x < x2 ) = ∫ f ( x) dx
x1
- это вероятность того, что числовое значение величины x (которая называется случайной величиной) находится в пределах x1<x<x2. В этом случае если интервал Dx=x2-x1 имеет малую вели-
чину, то p ( x1 < x < x2 ) » f ( x0 )×Dx , где x1<x0<x2.
+∞
Среднее значение величины в этом случае ищется в виде  x
x = ∫ x × f ( x) dx .
= ∫ x × f ( x) dx .
−∞
Функция f(x) называется плотностью распределения. Для неё выполняется условие нормировки
+∞
∫ f ( x) dx = 1 .
−∞
Смысл этого условия можно определить из равенства p (-¥ < x < ¥) = 1 - вероятность того, что
случайная величина примет хоть какое-то значение равна 1.
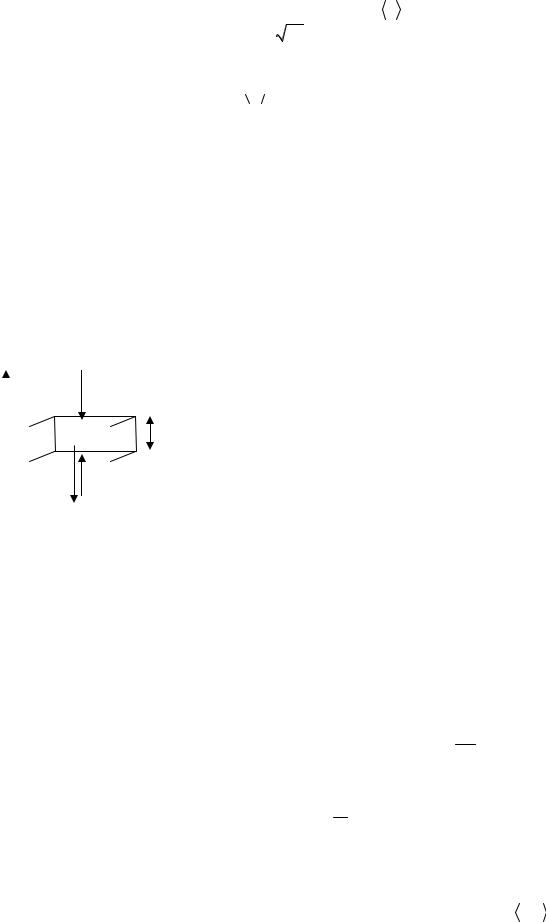
Примером плотности распределения является нормальное распределение (распределение Гаусса)
1й курс. 2й семестр. Лекция 15 |
2 |
||||||||
f ( x) = |
1 |
|
|
|
( x - x |
) |
|||
|
|
|
exp |
- |
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
s 2p |
|
|
|
2s |
2 |
|
|
|
|
|
|
|
|
|
|
|||
Если задана какая-то функция от случайной величины j(x), то среднее значение этой функции
+∞
 j
j = ∫ j( x)× f ( x) dx .
= ∫ j( x)× f ( x) dx .
−∞
Если при измерениях получаются две случайные величины x и y, то вероятность задается с помощью уже двумерной функции распределения
y2 x2
p ( x1 < x < x2 , y1 < y < y2 ) = ∫ ∫ f ( x, y) dxdy .
y1 x1
Если случайные величины x и y независимы друг от друга, то f ( x, y ) = f1 ( x)× f1 ( y ) .
Замечание. В случае, когда случайная величина задается функцией распределения вероятность
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
того, что она примет конкретное значение равна нулю |
|
p ( x = x0 ) = ∫ f ( x) dx = 0 . |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
Распределение Больцмана. |
|
|
|
|
|||||||||||
|
Пусть идеальный газ находится во внешнем поле силы тяжести при постоянной темпера- |
|||||||||||||||||||||
|
|
|
|
|
|
|
туре. Рассмотрим равновесие малого объёма газа |
|
|
|||||||||||||
z |
(p+dp)S |
|
|
|
|
pS - dmg - ( p + dp) S = 0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
−dpS = ρSdzg |
|
|
||||||||||||
|
|
|
|
|
|
dz |
где плотность газа r = |
|
m |
= |
pμ |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
V |
RT |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− μgz |
|
|
|||||||
|
|
|
|
|
|
|
|
|
pμ |
|
|
|
|
|
dp |
|
μg |
|
|
|||
|
pS |
|
|
-dp = |
dzg , |
= - |
dz , p = Ce RT |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
RT |
|
|
|
|
p |
RT |
|
|
|||||||||
|
dmg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− μgz |
|
|
|||
|
|
|
|
|
|
|
Задавая давление при z=0 p=p0, получаем p = p e RT . |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
μ |
|
|
|
|
|
|
|
|
|
Делим числитель и знаменатель на число Авогадро: m = |
- |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
N A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
масса молекулы, k = |
|
R |
|
- постоянная Больцмана |
|
|
|
|
|
|
|
|
|
|
|
|||||||
N A |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
− μgz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
− m0 gz |
|
|
|
|
||||||||
|
|
|
|
|
|
|
p = p e RT |
= p e |
|
kT |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
Это соотношение носит название барометрическая формула для изотермического столба газа в однородном поле силы тяжести.
Замечание. Хотя температура реальной атмосферы и уменьшается с высотой, но эта формула достаточно хорошо согласуется с экспериментом.
− m0 gz
С учётом основного уравнения МКТ p=nkT получаем n = n0e kT , где n0 – концентрация
молекул при z=0. Если учесть, что WП=m0gz – потенциальная энергия молекул в поле сил тяже-
сти, то получаем распределение Больцмана по энергиям
−WП kT .
Замечание. Из этой формулы следует, что при T®0 молекулы собираются вблизи поверхности
нулевого значения энергии Wп=0.
∑W
Найдем среднее значение потенциальной энергии молекул по высоте W = |
i |
|
. |
|
|
||
П |
N |
||
|
|
||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1й курс. 2й семестр. Лекция 15 |
|
|
|
|
|
|
|
|
|
|
3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
WП |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- непрерывная функция, то |
|
|
||||||||||||||||||||||||
Т.к. распределение молекул по энергиям n = n e kT |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m gz |
|
|
||||
¥ |
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
m0g×z |
|
|
|
|
n0 (kT ) |
2 |
¥ |
|
|
|
|
|
|
|
|
|
|
|
m0g×z |
|
|
|
|
t = |
0 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
m g × z |
|
|
|
- |
|
|
|
|
|
|
m gz |
|
|
|
kT |
|
||||||||||||||||
WS = ∫W ×n ×dz = ∫ m0g × z × n0e kT dz = |
|
|
|
|
|
∫ |
|
0 |
|
|
×e |
|
|
kT |
|
d |
0 |
|
|
= |
|
|
|
|
|
|
= |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m0g |
|
|
0 |
|
kT |
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = m g t |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||
|
n (kT )2 ¥ |
|
|
|
|
|
n |
(kT )2 |
|
|
|
|
¥ |
¥ |
|
|
|
|
|
|
|
n |
(kT )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
= |
0 |
|
∫t ×e-t dt = |
0 |
|
|
|
|
|
|
-t |
×e-t |
|
|
+ ∫ e-t dt |
= |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
m0g |
|
|
|
|
|
m0g |
|
|
0 |
|
|
|
|
|
m0g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m gz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
¥ |
¥ |
|
m0g×z |
|
|
|
|
|
|
|
|
¥ |
|
|
m0g×z |
|
|
|
|
|
|
|
|
|
|
t = |
|
|
|
0 |
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
n kT |
|
|
- |
|
|
|
m gz |
|
|
|
|
|
|
|
|
|
kT |
|
n kT |
|
|
|
|
|
n kT |
|
|
||||||||||||||||||
N = ∫ n × dz = ∫ n0e kT dz = |
|
0 |
|
|
|
∫ e |
|
kT |
|
d |
0 |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
0 |
|
∫ e-t dt = |
0 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
m0g |
0 |
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
|
|
m0g |
0 |
|
|
|
m0g |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = m g t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
n |
|
(kT )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
∑W |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
(kT )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
m0g |
|
|
|
|
n |
|
|
m g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Откуда |
W = |
i |
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
0 |
|
|
|
|
0 |
|
|
|
= kT . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
П |
N |
|
|
|
|
|
n0 kT |
|
|
|
|
|
|
m0g n0 kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m0g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Распределение Максвелла. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
Скорость любой молекулы v = (vx ,v y ,vz ) |
полностью задаётся трёмя коор- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
vz |
|
|
|
|
|
динатами. Поэтому её можно задать как точку в трехмерном пространстве |
||||||||||||||||||||||||||||||||||||||||||||||||||||
vскоростей. Тогда вероятность того, что координаты скорости молекулы будут находиться в определенных интервалах должна определяться через
плотность распределения скорости
vy |
|
v2 x v2 y v2 z |
||
< v y < v2 y ,v1z < vz < v2 z ) = ∫ ∫ ∫ f (vx ,v y ,vz )dvx dv y dvz . |
||||
|
p (v1x < vx < v2 x ,v1 y |
|||
vx |
|
v1x v1 y v1 z |
||
|
При этом должны быть выполнены условия нормировки |
|||
¥ ¥ ¥ |
(vx ,v y ,vz |
)dvx dv y dvz = 1 . |
||
|
∫ ∫ ∫ f |
|||
-¥ -¥ -¥ |
|
|
||
Так как каждая из координат скоростей не зависит от других, то плотность распределения |
||||
должна имеет вид |
|
|
||
|
f (vx ,v y ,vz ) = j(vx )×j(v y )×j(vz ) . |
|||
|
v2 x |
|
v2 y |
|
где p (v1x < vx < v2 x ) = ∫ j(vx ) dvx , |
p (v1 y < v y < v2 y ) = ∫ j(v y )dv y , |
|||
|
v1 x |
|
v1 y |
|
|
p (v1z < vz < v2 z ) |
v2 z |
||
|
= ∫ j(vz ) dvz . |
|||
|
|
|
v1 z |
|
Должны быть также выполнены условия нормировки |
||||
+¥ |
+¥ |
+¥ |
||
|
∫ j(vx ) dvx = 1, ∫ j(v y )dv y = 1, ∫ j(vz ) dvz = 1 . |
|||
-¥ |
-¥ |
-¥ |
||
Во всех интегралах считается, что проекция скорости принимается любые значения, вплоть до бесконечных. Очевидно, что это не так. Но если подынтегральные функции быстро убывают с ростом значений проекций скорости, то эта добавка будет вносить малую погрешность. Таким образом, к искомым функция предъявляется требование «быстрого убывания на бесконечности». Для поиска вида функции

1й курс. 2й семестр. Лекция 15 |
4 |
f (vx ,v y ,vz ) = j(vx ) ×j(v y ) ×j(vz )
мы применим принцип детального равновесия - в равновесной системе вероятность протекания прямого и обратного процесса одинаковые. Т.е. если формально обратить направление течения времени, то это не повлияет на протекание процессов в системе. Например, если в системе молекула движется в каком-то направлении, то при обращении времени она должны будет двигаться в обратную сторону. Но так как обращение не должно изменить состояния системы, то должна быть такая же молекула, которая до обращения времени уже двигалась в обратном направлении, следовательно, после обращения времени она будет двигаться в прямом направлении. Это означает, что искомая функция может зависеть только от величины скорости молекул,
т.е. от v = 
 v2 =
v2 = 
 v2x + v2y + v2z . Но в пространстве все направления равноправны. Если повер-
v2x + v2y + v2z . Но в пространстве все направления равноправны. Если повер-
нуть систему координат, то изменятся координаты вектора скорости, но не изменится длина вектора. Потребуем, чтобы функция f не меняла своё значение при повороте системы коорди-
нат. Таким образом, при v2 |
= v2x + v2y |
+ v2z = const должно быть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f (v) = j(vx ) ×j(v y ) ×j(vz ) = const |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Найдём градиент от искомой функции |
|
|
|
|
|
|
|
|
(v y ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
¶j(v |
x |
) |
|
×j(v y )×j |
(vz ); j(vx )× |
¶j |
×j(vz ); j(vx )×j(v y )× |
¶j(v |
z |
) |
|||||||||||||||||||||||||||||||
gradf = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||||
|
¶v |
|
|
|
|
|
|
¶v |
|
|
¶v |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
f (vx ,v y ,vz ) ¹ 0 ): |
|
z |
|
|
|
||||||||||||
Рассмотрим вектор, параллельный градиенту (учтем, что |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
gradf |
|
1 |
|
|
|
¶j(v |
x |
) |
1 |
|
|
|
¶j(v y ) |
1 |
|
|
|
¶j(v |
z |
) |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
f |
|
|
|
|
|
) |
|
¶v |
|
|
|
; j(v |
|
) |
|
|
¶v |
|
|
; j |
(v |
|
) |
|
¶v |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
= j(v |
x |
|
x |
|
|
y |
|
|
y |
|
z |
|
z |
|
|
. |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Т.к. v2 = v2x + v2y + v2z |
является функцией координат, то grad (v2 ) |
= |
(2vx ,2v y ,2vz ) . |
|
|
|
|
|||||||||||||||||||||||||||||||||||
В трехмерном пространстве скоростей поверхности уровней функций v2 и f являются концентрическими сферами с центром в начале координат, поэтому их векторы-градиенты параллельны в каждой точке, следовательно, пропорциональны друг другу:
gradf
f
В итоге из покоординатных равенств векторов получили систему уравнений
|
1 ¶j(vx ) |
|
|
= l2vx , |
1 ¶j(v y ) |
= l2v y , |
|
1 |
|
|
¶j(vz ) |
= l2vz . |
||||||||||||||||||||||||||||||||||||
|
j(vx ) |
|
¶vx |
|
|
j(v y ) |
|
|
|
¶v y |
|
j(vz ) |
|
|
¶vz |
|
|
|
||||||||||||||||||||||||||||||
После интегрирования |
|
|
|
) = C eλv2x , j(v |
|
) = C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
j(v |
x |
y |
eλv2y , j(v |
z |
) = C eλv2z . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Используем условие нормировки |
∫ C1eλv2x dvx |
= 1 . Этот интеграл - несобственный. Он сходится |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
только в том случае, когда число l - отрицательное l = - |
|
l |
|
. Интеграл |
∫ e− |
|
λ |
|
v2x dvx является |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|||
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
«табличным» ∫ e− |
|
λ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
vx dvx = |
|
|
|
|
|
, поэтому C1 |
|
|
= 1 или C1 = |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
l |
|
|
|
|
|
l |
|
|
|
|
p |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
На каждую степень свободы молекулы приходится энергия |
kT |
|
. Для идеального газа |
|||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
средняя кинетическая энергия одномерного движения равна |
|
|
mv2x |
|
|
= |
kT |
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
2 2

|
|
|
|
|
|
|
|
1й курс. 2й семестр. Лекция 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|||||||||||||||||
С другой стороны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
+∞ |
|
2 |
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
l ) = |
|
|
|
|
|
||||
mvx |
= ∫ C1 |
mvx e− λ v2x dvx |
= |
l m |
∫ v2x e− λ v2x dvx = |
|
1 1 m |
∫ l v2xe− λ v2x d (vx |
|
|
|
|
|
||||||||||||||||||||||||||||
|
2 |
−∞ |
|
2 |
|
|
p 2 |
−∞ |
|
|
|
|
|
|
|
|
|
p l 2 |
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
+∞ |
|
|
1 1 m p = m |
|
|
= kT . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
1 1 m ∫ t2e−t2 dt = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
p l 2 −∞ |
|
|
p l 2 2 |
|
4 l |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Откуда l = |
m |
и C1 = |
|
m . |
|
|
|
|
|
||||||||||||||
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
2pkT |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mv2x |
|
|
|
|
|
|
|
||
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому j(vx ) = |
|
m |
|
− |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
2kT |
. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2pkT |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mv2y |
|
|
|
|
|
||
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично j(v y ) |
= |
m |
|
− |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
2kT |
, |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mv2z |
2pkT |
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
j(vz ) = |
|
|
m |
|
− |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
-4 |
-3 |
-2 |
-1 |
0 |
|
1 |
2 |
|
|
|
|
3 |
|
|
4 |
|
|
2pkT |
e 2kT . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
−t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
ɶ |
|
|
|
|
|
|
|
|
|
|
|
В итоге получаем выражение для |
|||||||||||||||||||||||
|
|
|
|
|
|
|
p e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
График функции j(t ) = |
|
|
|
|
|
|
|
|
|
функции плотности распределения молекул |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по скоростям |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
m |
3 2 |
− mv2 |
|
|
m 3 2 |
−WК |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
f (v) = |
|
|
|
|
|
e 2kT |
= |
|
|
|
|
|
|
e kT . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2pkT |
|
|
|
2pkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Распределение молекул по абсолютному значению скорости. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Вероятность того, что величина скорости молекулы находится в каких-то пределах опре- |
|||||||||||||||||||||||||||||||||||||||
0,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
деляется выражением |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p (v1 < v < v2 ) = ∫∫∫ f (v) × dVv |
|
||||||||||||||||
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vv |
|
|
|
|
|
|
|
||
0,7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и не зависит от направления вектора ско- |
|||||||||||||||||||||
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рости. Поэтому в пространстве скоростей |
|||||||||||||||||||||
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неравенство v1 < v < v2 |
|
выделяет шаровой |
|||||||||||||||||||
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
слой в который попадают точки векторов |
|||||||||||||||||||||
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
скоростей Т.к. объем тонкого шарового |
|||||||||||||||||||||
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
слоя имеет вид |
dV |
= 4pv2 dv , то |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p (v1 < v < v2 ) = ∫ f (v)× 4pv2dv . |
||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
3,5 |
|
4 |
4,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
v1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
1 3 2 |
|
|
|
|
|
|
|
|
|
|
Поэтому подынтегральная функция |
|
||||||||||||||||||||||
|
|
|
|
|
ɶ |
|
|
t |
2 |
×e |
−t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
3 2 |
|
|
mv2 |
||||||
|
|
График функции |
F (t ) = 4p |
|
|
|
|
. |
|
|
|
F (v) = 4pv |
2 |
|
|
|
|
|
v |
2 |
− 2kT |
||||||||||||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
× f (v) = 4p |
|
|
|
|
|
×e |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2pkT |
|
|
|
|
|
|||
называется функцией распределения молекул по абсолютным значениям скоростей. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Максимум этой функции соответствует наиболее вероятной скорости: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
F ¢(v) |
|
|
|
|
|
|
m |
|
3 |
2 |
2 |
|
− |
mv2 |
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
= 4p |
|
|
|
|
|
×e 2kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2pkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
− mv2 |
mv |
|
v |
2 |
|
− mv2 |
|
|
|
|
- |
m |
v |
2 |
|
|
− mv2 |
= 0 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2v ×e 2kT - 2 |
|
|
|
|
×e 2 kT = 2v 1 |
|
|
|
|
×e |
2kT |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
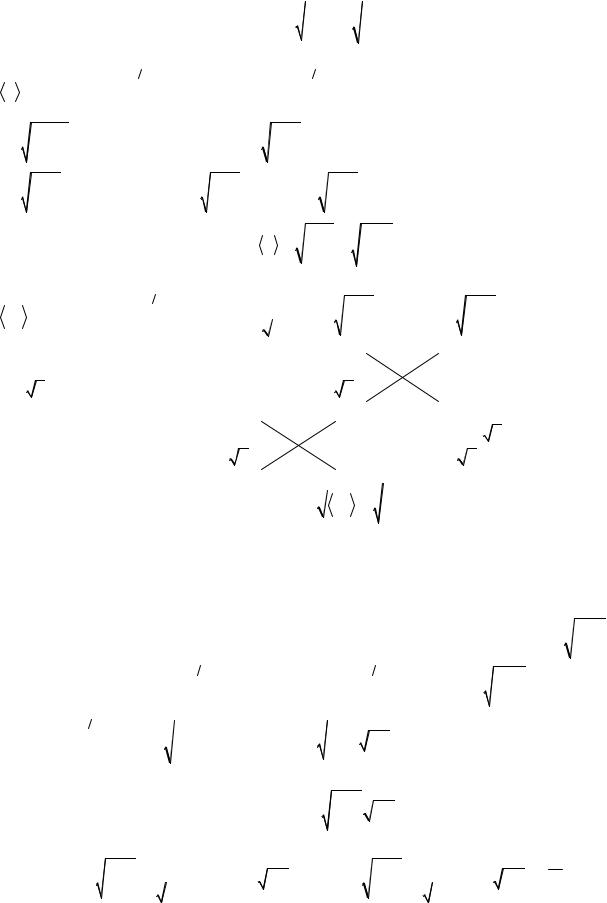
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1й курс. 2й семестр. Лекция 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vвер |
|
= |
|
|
|
|
|
2kT |
= |
|
|
|
|
|
|
2RT |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Найдём среднее значение скорости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
∞ |
|
|
|
|
|
m |
|
|
3 2 |
|
|
|
2 |
|
|
|
− |
mv2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 3 2 ∞ |
|
2 |
|
|
|
|
|
|
− |
mv2 |
|
|
|
|
|
|
(v |
2 |
) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
v = ∫ v × 4p |
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
×e 2kT dv = |
2p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ v |
|
|
×e 2kT d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
2pkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2pkT |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2kT ∞ mv2 |
|
|
|
|
− |
mv2 |
|
|
mv2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dp = e−t dt , p = -e−t |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
×e 2kT d |
|
|
|
|
|
|
|
|
|
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t ×e−t dt = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
2pkT |
|
|
|
|
|
|
|
∫0 2kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
|
pm ∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q = t,dq = dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(-e−t |
|
|
|
|
) = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
|
∞ |
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
= |
2 |
|
|
-te−t |
|
|
+ ∫ e−t dt |
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
pm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
= |
|
|
|
|
8kT |
|
= |
|
|
|
|
|
8RT |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pm |
|
|
|
|
|
|
|
|
|
|
pm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Найдём средний квадрат скорости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
∞ |
|
|
|
× 4p |
|
|
|
|
|
|
|
|
3 2 |
|
|
|
|
|
|
|
− mv |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 2kT |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
− mv |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
v2 = |
v2 |
|
|
|
|
|
|
v2 |
×e |
|
|
|
|
|
dv = 4 |
|
|
|
|
|
|
|
|
|
v ×e |
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
v = |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p m |
|
|
∫ |
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2pkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
8kT |
|
∞ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
dp = t ×e− |
|
|
|
dt , p |
= - |
|
|
|
e− |
|
|
|
|
|
|
|
8kT |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
∞ |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
∫t 4 ×e−t |
|
dt |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
t |
3e−t |
|
|
|
|
|
|
|
|
+ |
|
|
|
∫t2 ×e−t dt |
= |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
m p |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
p |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,dq = 3t |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q = t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
dp |
= t |
×e−t |
dt, p = - |
|
|
|
e−t |
|
|
|
|
|
|
|
3 8kT |
|
|
|
|
1 |
|
|
|
|
|
|
|
−t |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
∞ |
−t2 |
|
|
|
|
|
|
|
|
3 8kT |
|
p |
|
|
3kT |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ e |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
t |
×e |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
dt |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 m p |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 m |
|
|
p |
2 |
|
|
|
|
m |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
q = t ,dq = dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Поэтому средняя квадратичная скорость vкв = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
3kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
совпадает с уже известным выра- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
жением. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Найдём распределение молекул по кинетической энергии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p (WК1 < WК < WК 2 ) |
|
|
WК 2 |
|
|
|
|
|
(WК ) dWК |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫ f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
WК1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mv2 |
|
|
|
|
|
|
|
|
|||||
Используя формулу распределения по скоростям и учитывая, что WК = |
|
|
|
v = |
2W |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
и |
К |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
m |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v2 |
|
|
m |
|
|
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
− mv2 |
|
dv = 4p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2 v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−WК |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
p (v < v < v |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
2WК |
|
|
|
|
|
|
|
|
2WК |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
∫ |
4p |
|
|
|
|
|
|
|
|
v2 ×e |
2kT |
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
×e |
kT |
d |
|
|
|
|
= |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v1 |
|
|
2pkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2pkT |
|
|
|
|
|
v1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
m |
|
|
3 2 v2 |
2W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
= |
4p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К |
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e kT dWК = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
WК e kT dWК |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
kT |
|
|
|
|
|
pkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2pkT |
|
|
|
|
m 2 mW |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
WК |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(W |
|
|
) = |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W e kT . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
К |
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
pkT |
|
|
|
|
|
|
|
|
К |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Наиболее вероятная кинетическая энергия соответствует максимуму плотности распределения
|
|
|
|
|
|
|
|
|
|
− |
WК |
|
|
|
|
− |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢ (W |
) = |
2 |
1 |
|
1 |
|
1 |
|
|
|
2 |
|
|
|
1 |
|
1 |
|
1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
F |
|
|
e kT |
- |
W e kT |
= |
|
|
|
|
|
- |
W |
e |
|||||||||||||||||||||
|
|
|
|
|
kT |
|
|
|
|
|
kT |
||||||||||||||||||||||||
W |
К |
|
kT pkT |
2 W |
|
|
|
|
К |
|
|
|
|
|
kT pkT |
2 W |
|
|
К |
||||||||||||||||
|
|
|
|
|
|
|
|
|
К |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
= |
kT |
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К вер |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
−WК kT
= 0 ,
|
|
1й курс. 2й семестр. Лекция 15 |
|
7 |
||
Экспериментальная проверка распределения Максвелла |
||||||
Первым экспериментальным подтверждением распределения молекул по скоростям |
||||||
можно считать результаты опыта Штерна, описанного выше. Но точность этого опыта была не- |
||||||
1 |
2 |
|
3 |
ϕ |
4 |
|
|
|
|
|
6 |
|
5 |
|
|
|
L |
|
|
|
Схема опыта Ламмерта: 1 – печь; 2 – коллиматор; 3 – |
узкие |
|||||
щели; 4 – |
траектория молекул; 5 – |
детектор; быстро вра- |
||||
щающиеся диски |
|
|
|
|
|
|
достаточной для установления конкретного вида распределения. |
|
|||||
Прямые измерения скорости атомов ртути в пучке были выполнены в 1929 году Ламмер- |
||||||
том. Идея опыта заключалась в следующем. |
|
|
|
|
||
Атомы легкоплавкого металла, разогретого до высокой температуры, вылетали из печи |
||||||
1, проходили коллиматор (направляющие щели) 2 и по траектории 4 попадали на соосные бы- |
||||||
стровращающиеся диски 6, в которых сделаны щели 3, повернутые на угол ϕ, а затем регистри- |
||||||
ровались детектором 5. (В дисках было сделано несколько щелей для увеличения интенсивно- |
||||||
сти). Вся система находилась в вакуумированной камере. |
|
|
||||
Атомы могли пролететь щели в дисках, если величина их скорости попадала в опреде- |
||||||
лённый интервал [v0- |
v1, v0+ v2], где скорость v0, определялась из равенства |
|||||
|
|
L = |
ϕ |
|
|
|
|
|
v |
0 |
ω |
|
|
|
|
|
|
|
|
|
2 |
|
L - расстояние между вращающимися дисками, а величины |
||||
|
v1 , v2 определялись размерами щелей, геометрией пучка |
|||||
|
|
|||||
1 |
|
и т.д. |
|
|
|
|
|
|
Изменяя угловую скорость вращения дисков ω мож- |
||||
|
|
но было отбирать из пучка молекулы, имеющие определен- |
||||
|
|
ную скорость v, и по регистрируемой детектором интен- |
||||
|
|
сивности судить об относительном содержании их в пучке. |
||||
|
h |
Таким способом удалось экспериментально прове- |
||||
|
рить статистический закон распределения молекул по ско- |
|||||
|
|
|||||
|
|
ростям. Позже, когда при создании ядерного оружия воз- |
||||
L |
|
никла необходимость выделения нейтронов с определенной |
||||
|
3 |
кинетической энергией, подобная схема была применена в |
||||
|
устройстве, названным нейтронным монохроматором, по- |
|||||
Схема опыта Эстермана. |
зволяющим получать энергетические спектры нейтронов. |
|||||
1 – печь; 2 – диафрагма с узкой |
Несколько иначе был организован эксперимент по |
|||||
щелью; 3 – детектор. |
определению распределения по скоростям для атомов це- |
|||||
|
|
зия, выполненный в 1947 году немецким физиком - экспе- |
||||
риментатором Иммануэлем Эстерманом совместно с Симпсоном и Штерном. В эсперименталь- |
||||||

1й курс. 2й семестр. Лекция 15 |
8 |
ной установке пучок атомов цезия вылетал через отверстие в печи 1 с некоторой скоростью v и под действием силы тяжести начинал двигаться по параболе. Атомы, прошедшие через узкую щель в диафрагме 2, улавливались детектором 3, который можно было располагать на различных высотах h. Величина отклонения h пучка в гравитационном поле Земли зависела от скорости атома. В этих опытах отклонение h составляло величину порядка нескольких долей миллиметра при расстоянии L от печи до детектора равном 2 метрам. Перемещая датчик и регистрируя количество атомов цезия, попадающих в детектор за единицу времени, можно было построить зависимость интенсивности пучка от величины h. Последующий пересчет, с учетом известной зависимости высоты h от скорости атома v, давал распределение по скоростям атомов цезия.
Все проведенные эксперименты подтвердили справедливость полученного Максвеллом распределения по скоростям для атомных и молекулярных пучков.
Распределение Максвелла-Больцмана.
Если ввести 6-мерное пространство, координатами молекулы в котором являются вели-
чины ( x, y, z,vx ,v y ,vz ) , то функция распределения в таком пространстве будет зависеть от этих шести переменных: n f ( x, y, z,vx ,v y ,vz ) . Считая пространственные переменные ( x, y, z ) и ком-
поненты скорости (vx ,v y ,vz ) статистически независимыми друг от друга, можно записать функцию распределения в этом шестимерном пространстве:
n f ( x, y, z,vx ,v y ,vz ) = n ( x, y, z ) × f (vx ,v y ,vz ) .
Эта функция называется распределением Максвелла-Больцмана
|
|
m 3 2 |
− |
WП +WК |
|
|
n f (x, y, z,vx ,v y |
,vz ) = n0 |
|
|
e kT . |
||
|
||||||
|
|
2pkT |
|
|
|
|
Замечание. При получении распределения Максвелла-Больцмана предполагалось, что температура газа не зависит от координаты точки. В частности, температура газа на всех высотах над поверхностью Земли при термодинамическом равновесии должна быть одинаковой. С этим утверждением связан парадокс, всесторонне рассмотренный Максвеллом. Дело в том, что при движении вверх молекулы газа должны затрачивать свою кинетическую энергию на преодоление силы тяжести, и поэтому их средняя кинетическая энергия (а, следовательно, и температура) должна уменьшаться. Но этого не происходит вследствие того, что при этом не все молекулы, из-за недостатка их кинетической энергии, смогут преодолеть силу тяжести. Молекулы, имеющие недостаточную кинетическую энергию, не могут подняться высоко, что приведет, в соответствии с распределением Больцмана, к уменьшению их концентрации с высотой. Поэтому температура газа останется неизменной.
Функция распределения в случае, когда кинетическая энергия зависит только от скоро-
сти v , а потенциальная - только от радиус-вектора r |
частицы, имеет вид: |
|
|
|||||||||
|
1 |
W |
(r ) +W |
(v) |
|
W |
(r ) +W |
(v) |
||||
f (r ,v) = |
|
exp - |
П |
К |
|
, где Q = ∫ ∫ exp - |
П |
К |
|
dVdVv . |
||
Q |
|
kT |
|
|
kT |
|
||||||
|
|
|
|
|
Vv V |
|
|
|
|
|||
Здесь V - объем, занимаемый системой в координатном пространстве, Vv - соответствующий объем в пространстве скоростей. Формула позволяет описывать равновесное распределение для достаточно произвольной термодинамической системы.
Полученные выше функции распределения описывают случай, когда полная энергия частицы W принимает непрерывный ряд значений. При статистическом описании системы, частицы которой могут принимать только некоторый дискретный набор значений энергии W1, W2, W3, …, W m, необходимо использовать вместо функции распределения вероятность P(Wi) нахождения частицы в состоянии со значением энергии Wi: В случае дискретных состояний можно записать следующее выражение для этой вероятности P(Wi):
P (Wi ) = |
1 |
|
|
W |
m |
|
|
W |
||
|
exp |
- |
i |
|
, где Q = ∑exp |
- |
i |
. |
||
Q |
|
|
||||||||
|
|
|
kT |
i=1 |
|
|
kT |
|||

1й курс. 2й семестр. Лекция 15 |
9 |
Эта формула называется распределением Больцмана для дискретных состояний. Если полное число частиц в системе равно N, то количество частиц Ni в состоянии с энергией Wi определяется по формуле: Ni = P (Wi ) N .
Равновесные флуктуации.
Флуктуации – это случайные отклонения какого-либо параметра термодинамической системы от его среднего значения. Флуктуации возникают из-за хаотического теплового движения частиц термодинамической системы. В любой, даже равновесной системе существуют случайные отклонения от средних значений параметров, которые можно экспериментально наблюдать при долговременных измерениях. Например, флуктуации давления проявляются в броуновском движении малых твёрдых частичек, взвешенных в жидкости.
Если среднее значение некоторого параметра x равно <x>, то флуктуация этого параметра определяется как отклонение значения от среднего
Dx = x -  x
x
Очевидно, что среднее значение флуктуации равно нулю  Dx
Dx =
=  x -
x -  x
x
 =
=  x
x -
-  x
x = 0 .
= 0 .
Однако средний квадрат уже, вообще говоря, не равен нулю
 (Dx)2
(Dx)2  =
=  ( x -
( x -  x
x )2
)2  =
=  x2 - 2x
x2 - 2x  x
x +
+  x
x 2
2  =
=  x2
x2 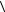 - 2
- 2  x
x
 x
x +
+  x
x 2 =
2 = 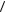 x2
x2  -
-  x
x 2 .
2 .
Аналогично, для некоторой функции параметра j( x)
 (Dj( x))2
(Dj( x))2  =
= 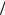 (j( x))2
(j( x))2  -
-  j( x)
j( x)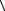 2 .
2 .
|
|
|
|
(Dj( x))2 |
|
Величина (Dj( x))2 называется средней квадратичной флуктуации, а |
|
- сред- |
|||
|
|
||||
|
j( x) |
||||
|
|
|
|
|
|
ней квадратичной относительной флуктуации.
Флуктуациям в равновесном состоянии подвержены и внутренняя энергия, и давление, и температура и т.д. Для всех термодинамических параметров их относительные флуктуации обратно пропорциональны корню из числа частиц в системе:
(Dx)2 |
b . |
= |
|
x |
N |
Коэффициент можно принимать за единицу b=1 при оценочных расчетах.
Пример. Оценить относительные равновесные флуктуации температуры газового термометра, содержащего один моль газа.
Решение. Для одного моля N = 6,022 ×1023 моль-1. Тогда |
|
(DT )2 |
= |
|
1 |
|
»1,29 ×10−12 . Очевид- |
|
|
|
|||||
|
|
|
|
||||
|
|
T |
|
|
N |
||
но, это очень малая величина.
Статистическое обоснование второго начала термодинамики.
Для равновесных систем вероятность возникновения флуктуации обратно пропорциональна её величине – чем больше величина отклонения, тем меньше вероятность её возникновения. Например, вероятность того, что все молекулы газа соберутся в одной части сосуда очень мала, т.е. процесс самопроизвольного перехода в неравновесное состояние маловероятен, что согласуется со вторым началом термодинамики. Всякий самопроизвольный необратимый процесс переводящий систему из неравновесного состояния в равновесное с гораздо большей вероятностью протекает в природе, чем обратный ему процесс. Необратимыми являются те процессы, вероятность протекания которых в прямом направлении выше, чем в обратном. Это

1й курс. 2й семестр. Лекция 15 |
10 |
приводит к возникновению в природе преимущественного направления протекания термодинамических процессов. Термодинамической величиной, характеризующей направление протекания процесса, является энтропия.
Пусть в сосуде, объем которого V0 находится одна молекула. Тогда вероятность того,
что она будет находиться в части сосуда, объём которой V, равна p (V ) = V . Если молекул две,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
||||||
то p (V ) = |
V |
|
, а если их число равно N, то |
p (V ) = |
V |
|
. Поэтому отношение вероятностей |
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||
V0 |
|
|
|
|
p (V ) |
|
|
|
|
|
|
|
|
V0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
V N |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
для разных объёмов равно |
|
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p (V ) |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С другой стороны, рассмотрим изотермическое расширение идеального газа от объёма |
||||||||||||||||||||||||
V1 до объёма V2. В этом случае dU=0, поэтому dQ=dA=nRT×dV. Следовательно, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
V2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
S2 - S1 = ∫ dQ = |
∫ nR |
dV |
= nR ln |
V2 |
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 T |
V |
|
|
V |
|
|
V1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
p (V2 ) |
|
|||
|
|
|
|
N |
|
|
|
|
V |
N |
|
|
|
|||||||||||
Однако, nR = |
|
|
|
|
R = Nk , поэтому S2 - S1 = k ln |
2 |
= k ln |
|
|
|
|
|
. |
|||||||||||
|
N |
|
V |
|
p (V ) |
|||||||||||||||||||
|
|
|
|
|
A |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|||||
Из этой формулы следует, что энтропия состояния пропорциональна вероятности того, что система придет в это состояние.
Статистическим весом G макроскопического состояния называется величина, численно равная количеству равновесных микросостояний, с помощью которых может быть реализовано рассматриваемое макросостояние. Статистический вес пропорционален вероятности G ~ p. Если система состоит из N частиц, каждая из которых может находится в одном из К дискретных
состояниях, то статистический вес системы равен G = |
N ! |
||||||
|
, а соответствующая веро- |
||||||
|
|||||||
|
|
|
|
|
N1 ! N2 ! ...N2 ! |
||
|
N ! |
|
|
|
K |
||
ятность p = |
− N , где Ni – |
число частиц в состоянии с номером i, и ∑ Ni = N . |
|||||
|
K |
||||||
|
|||||||
|
N1 ! N2 ! ...N2 ! |
|
|
|
i=1 |
||
Данное рассуждение может служить обоснованием для формулы Больцмана, связывающей энтропию со статистическим весом
S = k ln G .
Замечание. Для статистической энтропии также выполняется закон аддитивности - если систему разбить на две невзаимодействующие между собой части, то G = G1 ×G2 и
S = k ln G = k ln G1 + k ln G2 = S1 + S2 .
Замечание. С законом возрастания энтропии связана «тепловая смерть» Вселенной, т.е. состояние с максимальной энтропией и максимальным статистическим весом. Но в такой системе должны происходить флуктуации. Сегодняшнее состояние Вселенной является такой флуктуацией.
