Санкт-Петербургский государственный политехнический университет

Кафедра информационная машиностроительная технология

Отчет

по лабораторной работе № 13 (вариант 1)

Дисциплина: Вычислительная математика

Тема: Решение плоской задачи теории упругости МКЭ

Студент гр. 2041/3: Бондаренко Е.

Преподаватель: Кожанова Ю. В.

______________ 2008 г.

Санкт-Петербург

2008

Цель работы:

Изучение метода конечных элементов на примере решения плоской задачи теории упругости с использованием линейных треугольных элементов.

Исходные данные:

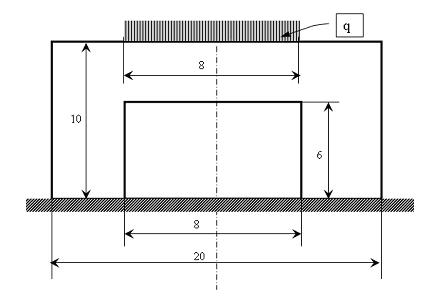
Толщина детали b=1

h1=10

h2=6

d1=20

d2=8

d_q=8

μ=0,25

q=-10000

Е=10⁷

Выполнение задания:

Так как деталь симметрична, а действующая сила находится на оси симметрии, то можем строить сетку только для половины детали.

Таблица 1. Координаты узлов фрагментов (Mf = 2, Mn = 14)

Номер узла j	Координаты узлов		Номер узла j		Координаты узлов
	Xj	Yj			Xj	Yj
1	0	6	8		10	10
2	0	8	9		4	3
3	0	10	10		10	5
4	2	6	11		4	0
5	5	10	12		7	0
6	4	6	13		10	0
7	7	8

Таблица 2. Соединение объектов

Номер фрагмента	Стороны фрагментов
	1	2	3	4
1	2	0	0	0
2	0	0	1	0

Таблица 3. Данные о разбиении фрагментов и связь глобальных и локальных номеров узлов

Номер фрагм.	ξ строки	η столбцы	1	2	3	4	5	6	7	8
1	9	9	6	7	8	5	3	2	1	4
2	9	9	11	12	13	10	8	7	6	9

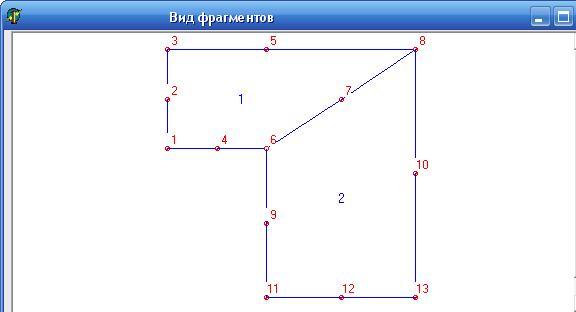
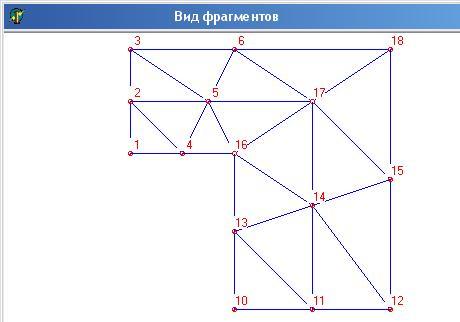
Разбиения 3х3:

В данной таблице слева выводятся перемещения узлов сетки, справа – значения перемещений.

Далее увеличим количество разбиений на 5х5:

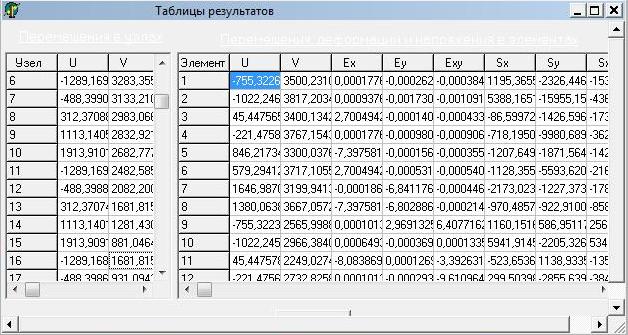
Увеличим количество разбиений на 7х7:

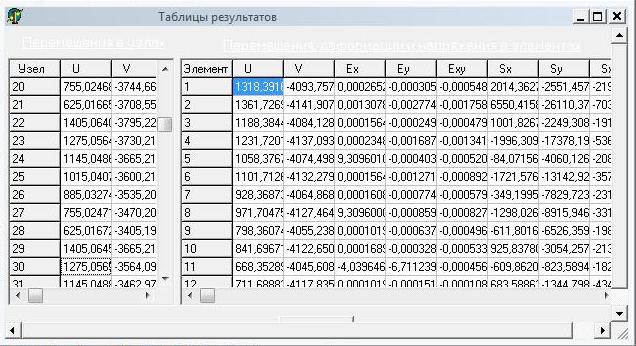
Выполнение в MAthCad:

Координаты узлов и соответствующие им значения перемещений.

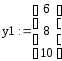
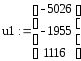
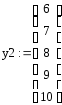
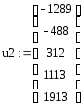
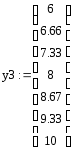
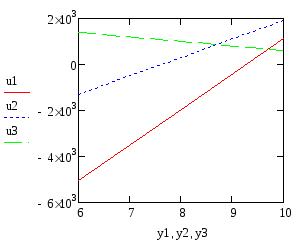
График зависимости значений перемещений от координат узлов:

Вывод:

Программа значительно упрощает решение плоской задачи плоской упругости. Однако данные о сетке элементов требуют подготовки большого объема информации, неверно заданная информация об элементах является источником значительных ошибок при решении задач методом конечных элементов.

Ответы на контрольные вопросы:

1)В качестве фрагментов используют четырехугольные элементы с восемью узлами

2)Каждый фрагмент отображается на квадрат с локальными координатами ,. Начало координат , выбирается в центре квадрата. Координаты  и  изменяются от -1 до 1. Такая система координат называется естественной.

3) Область, в которой ищется решение предварительно разбивается на несколько фрагментов. Начало координат выбирается произвольно. Выбранная система координат называется глобальной

4) Узлы на общей стороне фрагментов должны иметь одинаковые номера

5) В локальной системе координат фрагмент разбивается на прямоугольнике

Полученные в локальной системе координат новые узловые точки отображаются обратно в глобальную систему координат по формулам

6) В качестве фрагментов используют четырехугольные элементы с восемью узлами. Функции Ni представляют собой полиномы второго порядка относительно локальных координат  и . Поэтому отображение

будет квадратичным, а стороны элементов - параболы.

7) Функции формы в выражении (*) для квадратичного отображения имеют вид

N1=-0.25*(1-)*(1-)*(++1); N3= 0.25*(1+)*(1-)*(--1); N5= 0.25*(1+)*(1+)*(+-1); N7=-0.25*(1-)*(1+)*(-+1);

N2 = 0.5*(1-2)*(1-); N4 = 0.5*(1-2)*(1+); (26) N6 = 0.5*(1-2)*(1+); N8 = 0.5*(1-2)*(1-).

Ni(,) - функции формы

8) Дискретная модель области обычно конструируется из нескольких четырехугольных фрагментов, имеющих общие стороны. При переходе к новому фрагменту необходимо проверять каждую сторону на связность с другими фрагментами. Информация о соединении фрагментов задается матрицей связности. Количество строк в матрице равно числу фрагментов. Количество столбцов равно 4(число сторон фрагмента). Если сторона не связана, то в строке матрицы связности, соответствующей номеру фрагменту и в колонке, соответствующей номеру стороны записывается 0. В противном случае записывается номер фрагмента, с которым граничит сторона. Узлы на общей стороне фрагментов должны иметь одинаковые номера.

9) Количество разбиений фрагмента зависит от требуемой точности вычислений напряженно-деформированного состояния. Заданную область предварительно разбивают на четырехугольные фрагменты с восьмью узлами.

10)В качестве граничных условий задаются границы поверхностные силы, границы сосредоточенные силы и - перемещения.

11)Интерполяционный полином должен быть первого порядка

12) E – модуль упругости , - коэффициент Пуассона. Предполагается, что материал изотропен.

13)Напряженно – деформированное состояние тела в плоской задачи теории упругости характеризуется компонентами напряжений и деформаций.

Для плоского деформированного состояния компоненты тензора деформаций

, компоненты тензора напряжений .

14)В методе конечных элементов неизвестная функция, являющаяся решением заданного дифференциального уравнения, аппроксимируется множеством полиномов, определенных на конечном числе подобластей, называемых конечными элементами.