1. ОБЩИЕ СВЕДЕНИЯ
1.1. Основные положения
Обыкновенным дифференциальным
уравнением называется
уравнение, которое связывает независимую
переменную
,
неизвестную функцию
этой переменной и ее производные
:
,
(1.1)
где
- функция указанных в скобках аргументов,
заданная в некоторой области их изменения.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
Если в уравнении (1.1) функция
такова, что это уравнение можно представить
в виде:
,
(1.2)
то такое уравнение называется
обыкновенным дифференциальным уравнением
-го
порядка, разрешенным
относительно старшей производной.
Уравнение называется линейным,
если функция
линейна относительно искомой функции
и ее производных.
Решением
дифференциального уравнения
-го
порядка называется функция
,
непрерывная на некотором интервале
вместе со своими производными до
порядка включительно, имеющая производную
и такая, что подстановка
в уравнение обращает его в тождество.
График решения дифференциального
уравнения называется интегральной
кривой.
1.2. Задача Коши
Задача Коши является одной из важнейших задач в теории и приложениях дифференциальных уравнений. В данной задаче необходимо найти решение дифференциального уравнения, удовлетворяющего заданным начальным условиям. Поэтому задача Коши еще называется начальной задачей. Для уравнения (1.2) она записывается в следующем виде:
,
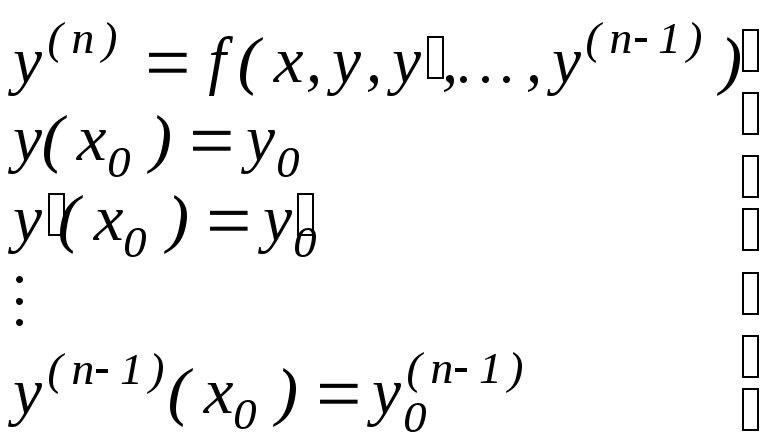(1.3)
где
- заданные числа.
Существование решения и его единственность определяет теорема Коши:
«Пусть будут выполнены следующие условия:
а) функция
определена и непрерывна в некоторой
замкнутой области
,
а также имеет в
ограниченные частные производные по
переменным
;
б) точка (
)
лежит внутри области
.
Тогда решение задачи Коши (1.3) существует и единственное».
Общим решением дифференциального
уравнения
-го
порядка в некоторой области, принадлежащей
области
,
называется функция
,
зависящая от
произвольных постоянных, и такая, что
при подстановке в уравнение она обращает
его в тождество при любых значениях
.
Геометрически общее решение в этой
области представляет семейство
непересекающихся интегральных кривых,
полностью покрывающих всю область.
Общим интегралом дифференциального уравнения называется соотношение вида
,
(1.4)
которое неявно определяет общее решение.
При конкретных значениях
,
включая и ± ∞, из общего решения
выделяется частное решение, а общий
интеграл становится частным интегралом.
В каждой точке (
)
частного решения или частного интеграла
выполняются условия теоремы Коши.
Для решения задачи Коши могут применяться
как аналитические, так и численные и
приближенно-аналитические методы
решения. Последние методы в отличие от
аналитических позволяют найти искомую
функцию
лишь приближенно. Но при этом численные
методы являются более универсальными,
так как с их помощью можно приближенно
решать многие из задач, точное решение
которых аналитическими методами не
могут быть найдены. Аналитическими
методами решаются только линейные
задачи и некоторые типы нелинейных
задач, в то время как для численных
методов эти ограничения отсутствуют.
Чтобы упростить рассмотрение и с учетом того, что численные методы легко обобщаются на системы уравнений, в дальнейшем будем рассматривать решение задачи Коши для уравнений первого порядка:
,
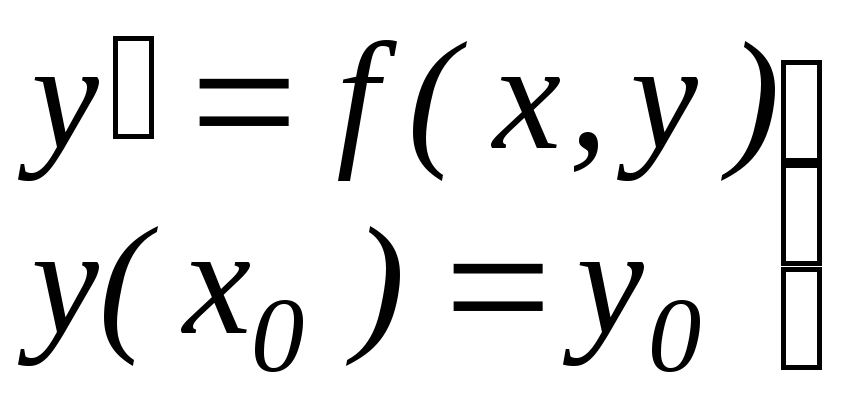(1.5)
При этом
.
Для численного решения весь диапазон
значений
разбивается на
интервалов. Границы интервалов образуют
узлы сетки
,
при этом
.
Расстояние между соседними узлами
называется шагом
интегрирования или
параметром сетки
.
Если этот параметр постоянный, то говорят
о равномерной
сетке, если переменный – о неравномерной.
Решение находится в виде
последовательности значений
,
являющихся приближением значений
точного решения
в узлах сетки
(рисунок 1.1).
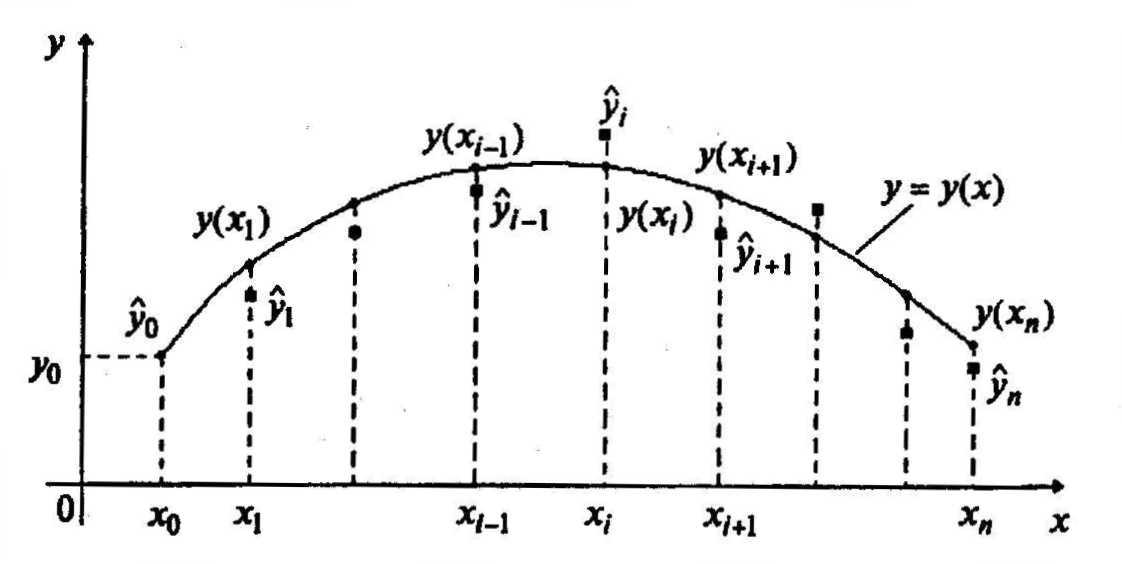
Рисунок 1.1 – Сеточное представление решения дифференциального уравнения
Численные методы решения обыкновенных дифференциальных уравнений делятся на две группы:
- дискретные методы, позволяющие найти решение только в узлах сетки. Эти методы еще называются разностными методами или методами сетки;
- непрерывно-дискретные методы, основанные на использовании дискретных методов и сплайн-функций для восполнения численных результатов. Они позволяют найти непрерывные решения дифференциальных уравнений.
Дискретные методы также подразделяются
на явные и неявные. Значение
на (
)-м
шаге может определяться явно:
,
(1.6)
где
- некоторая функция, зависящая от
конкретного метода. В данном случае
кроме последней рассчитанной точки
могут быть использованы еще (
)
предыдущих точек.
В выражении (1.6) искомая величина
присутствует только в левой части
уравнения. При неявном определении
параметра
на (
)-м
шаге выражение для этого параметра
следующее:
,
(1.7)
где искомая величина
присутствует как в правой, так и в левой
частях уравнения.
Явные и неявные методы делятся также
на одношаговые и многошаговые (
-шаговые).
В одношаговых методах для расчета
очередной точки (
)
требуется информация только о последней
рассчитанной точке (
).
В
-шаговых
методах для нахождения точки (
)
требуется информация и о
предыдущих точках.
Формулы (1.6) и (1.7) в общем случае представляют
собой нелинейные уравнения относительно
и называются разностными схемами.
Численный метод называется устойчивым, если численные результаты непрерывно зависят от входных данных и если погрешность остается ограниченной при заданных пределах изменения параметров численного алгоритма (шагов сетки, числа итераций и т.д.)
Сходимость приближенных методов
является основной проблемой, от успешного
преодоления которой зависит точность
решения всей задачи. Численный алгоритм
называется сходящимся, если при
стремлении его параметров к определенным
предельным значениям (например, при
или при
,
где
- число итераций) результаты стремятся
к точному решению.
Ниже рассмотрим основные дискретные методы решения обыкновенных дифференциальных уравнений.