
- •1.3. Передаточная функция системы элементарных звеньев
- •1.4. Структурные схемы с обратной связью
- •1.5. Преобразования структурных схем
- •1.6. Пример преобразования структурной схемы
- •1.7. Частотные характеристики системы
- •1.8. Анализ устойчивости систем автоматического регулирования
- •1.9. Алгебраические критерии устойчивости
- •1.10. Частотные критерии
1.7. Частотные характеристики системы
Если на вход линейной устойчивой системы длительно действует гармонически изменяющаяся сила, то после затухания переходных процессов на выходе установятся гармонические колебания с такой же частотой (рисунок 1.13). Однако амплитуда и начальная фаза их будут зависеть от динамических свойств системы. Запишем уравнение, связывающее входные и выходные величины:
![]() .
(1.38)
.
(1.38)

Рисунок 1.13 – Входной и выходной гармонические сигналы
Гармоническим сигналом
называется сигнал
![]() вида
вида
![]() (1.39)
(1.39)
или в комплексной форме
![]() .
(1.40)
.
(1.40)
Частным случаем такого сигнала являются сигналы
![]() ;
(1.41)
;
(1.41)
![]() .
(1.42)
.
(1.42)
Выражение (1.41) соответствует
случаю, когда
![]() ,
а выражение (1.42) – случаю, когда
,
а выражение (1.42) – случаю, когда
![]() .
.
Пусть входной сигнал имеет
фиксированную частоту. На комплексной
плоскости этот сигнал изобразится в
виде вектора с амплитудой
![]() ,
вращающегося против часовой стрелки
вокруг начала координат с частотой
,
вращающегося против часовой стрелки
вокруг начала координат с частотой
![]() .
Тогда на выходе получим гармонический
сигнал. Для удобства рассмотрения пусть
при
.
Тогда на выходе получим гармонический
сигнал. Для удобства рассмотрения пусть
при
![]() фаза входного сигнала
фаза входного сигнала
![]() .
Выходной сигнал тогда может быть
представлен на комплексной плоскости
в виде вектора с амплитудой
.
Выходной сигнал тогда может быть
представлен на комплексной плоскости
в виде вектора с амплитудой
![]() ,
сдвинутого на угол
,
сдвинутого на угол
![]() относительно вектора входного сигнала,
и вращающегося относительно начала
координат с той же частотой
относительно вектора входного сигнала,
и вращающегося относительно начала
координат с той же частотой
![]()
![]() .
(1.43)
.
(1.43)
Подставим выражения (1.39) и
(1.43) в выражение (1.38) при
![]() ,
получим
,
получим
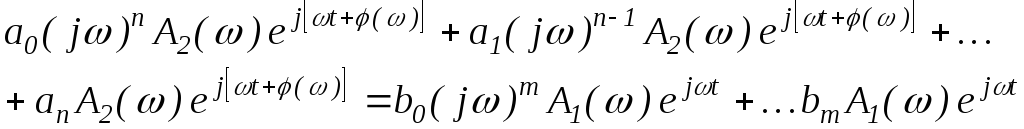 .
(1.44)
.
(1.44)
откуда
 (1.45)
(1.45)
Функция (1.45) называется
комплексным коэффициентом усиления
(при частоте
![]() ).
Формально комплексный коэффициент
усиления получается из передаточной
функции
).
Формально комплексный коэффициент
усиления получается из передаточной
функции
![]() при подстановке
при подстановке
![]() и является отношением выходного
гармонического сигнала к входному
гармоническому сигналу.
и является отношением выходного
гармонического сигнала к входному
гармоническому сигналу.
В вышеприведенных выражениях
![]() и
и
![]() - функции частоты при неизменной амплитуде
- функции частоты при неизменной амплитуде
![]() входного сигнала. Каждой фиксированной
частоте входного гармонического сигнала
будут соответствовать определенные
значения амплитуды выходного сигнала
и сдвига фазы.
входного сигнала. Каждой фиксированной
частоте входного гармонического сигнала
будут соответствовать определенные
значения амплитуды выходного сигнала
и сдвига фазы.
Комплексную функцию
![]() действительного переменного
действительного переменного
![]() можно представить в виде
можно представить в виде
![]() ,
(1.46)
,
(1.46)
где
 .
(1.47)
.
(1.47)
При каждом фиксированном
со значение
![]() однозначно определяет (рисунок 1.14) точку
на комплексной плоскости с декартовыми
координатами
однозначно определяет (рисунок 1.14) точку
на комплексной плоскости с декартовыми
координатами
![]() ,
,
![]() или полярными координатами
или полярными координатами
![]() ,
,
![]() .
.

Рисунок 1.14 – Графическое
представление функции
![]()
Следовательно, можно записать формулы перехода от полярных координат к декартовым, и наоборот:
 .
(1.48)
.
(1.48)
Зависимости
![]() ,
,
![]() ,
,
![]() ,
,
![]() (рисунок 1.15, а – г) называются частотными
характеристиками системы – амплитудной,
фазовой, вещественной и мнимой
соответственно.
(рисунок 1.15, а – г) называются частотными
характеристиками системы – амплитудной,
фазовой, вещественной и мнимой
соответственно.

Рисунок 1.15 – Частотные характеристики системы
Вектор-годограф
![]() ,
построенный на комплексной плоскости
(рисунок 1.16) при изменении частоты от
,
построенный на комплексной плоскости
(рисунок 1.16) при изменении частоты от
![]() до
до
![]() ,
называется амплитудно-фазовой частотной
характеристикой системы.
,
называется амплитудно-фазовой частотной
характеристикой системы.
Комплексный коэффициент
усиления и частотные характеристики
являются важными характеристиками
звена и системы, позволяющими исследовать
устойчивость и характер протекания
переходных процессов. Зная величину
![]() ,
можно определить реакцию линейной
системы не только на синусоидальный
входной сигнал, но и на любую другую
внешнюю силу, представленную в виде
интеграла Фурье, т.е. в виде бесконечной
суммы синусоидальных колебаний всех
частот. Зная, как проходит каждое из
этих колебаний через систему, и складывая
их на выходе, можно получить значение
выходной величины
,
можно определить реакцию линейной
системы не только на синусоидальный
входной сигнал, но и на любую другую
внешнюю силу, представленную в виде
интеграла Фурье, т.е. в виде бесконечной
суммы синусоидальных колебаний всех
частот. Зная, как проходит каждое из
этих колебаний через систему, и складывая
их на выходе, можно получить значение
выходной величины
![]() .
.

Рисунок 1.16 – Амплитудно-фазовая частотная характеристика
Частотные характеристики элементов системы и всей системы могут быть получены экспериментально с помощью генератора синусоидальных колебаний и соответствующей измерительной аппаратуры для измерения частоты, амплитуды и фазы колебаний. Полученные экспериментальные частотные характеристики являются одной из форм задания математической модели системы, которая может непосредственно использоваться в расчетах устойчивости и переходных процессов.
