2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОЛИНЕЙНОГО СТЕРЖНЯ

2.1. Статически определимые системы

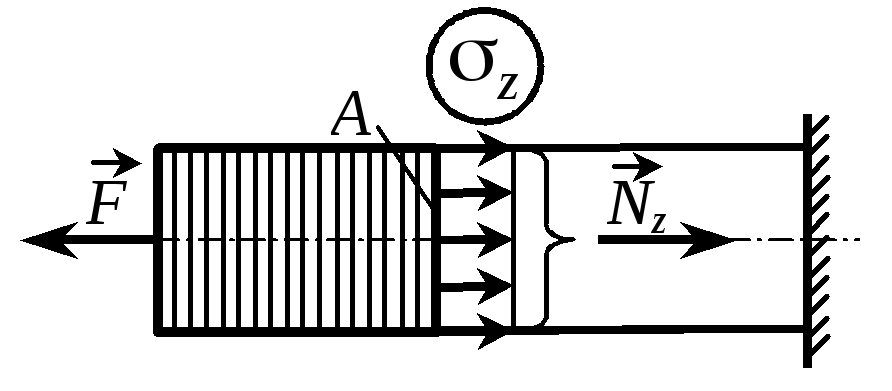
При центральном растяжении (сжатии) прямолинейного стержня в его поперечных сечениях возникает только один внутренний силовой фактор – п р о д о л ь н а я с и л а N_z.

С продольной силой связаны н о р м а л ь н ы е н а п р я ж е н и я, которые на достаточном удалении от точек приложения внешних сил

Рис. 2.1

равномерно распределяются по поперечному сечению (рис. 2.1).

_z = N_z / A (2.1)

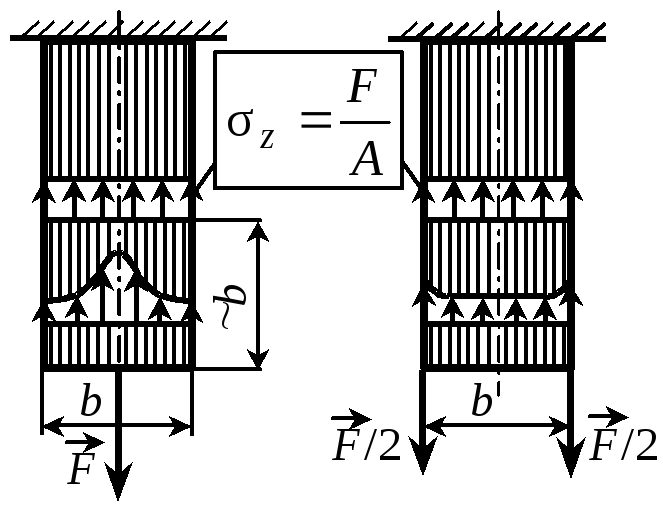
В местах приложения внешних сосредоточенных сил распределение напряжений значительно отличается от равномерного (рис. 2.2). Однако, как показывает опыт, на расстоянии, равном примерно наибольшему из поперечных размеров стержня b,

Рис. 2.2

распределение напряжений становится практически равномерным. Отмеченное свойство выражает принцип Сен – Венана: на достаточном удалении от места приложения сил распределение напряжений практически не зависит от способа приложения сил, а только от их статического эквивалента.

Условие прочности выражается неравенством

_max  , (2.2)

где  = _пред / П – допускаемое напряжение, П – коэффициент запаса прочности, _пред – предельное для данного материала напряжение, равное пределу текучести (_Т или _0,2) для пластичных материалов или пределу прочности _пч для хрупких материалов,

т.е.

В инженерных расчетах отклонения от основного неравенства (2.2) допустимы в ту или другую сторону в пределах  5 %.

Различают три вида расчета на прочность:

1. проверка прочности, 2) подбор сечения, 3) определение допускаемой нагрузки.

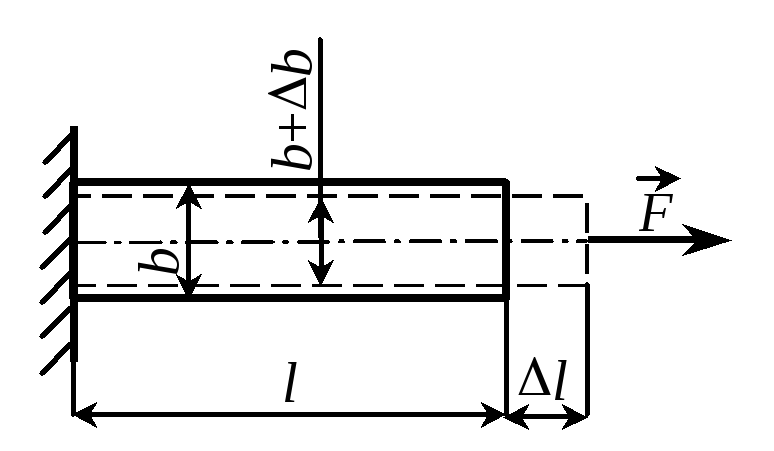
При растяжении (сжатии) возникают продольные  и поперечные  деформации, связанные между собой зависимостью (законом Пуассона):   , (2.3)

Рис. 2.3

где   l/l,   b/b,  - коэффициент Пуассона, который для различных материалов лежит в пределах от 0 до 0,5.

Нормальные напряжения  связаны с продольной деформацией  законом Гука   Е , (2.4)

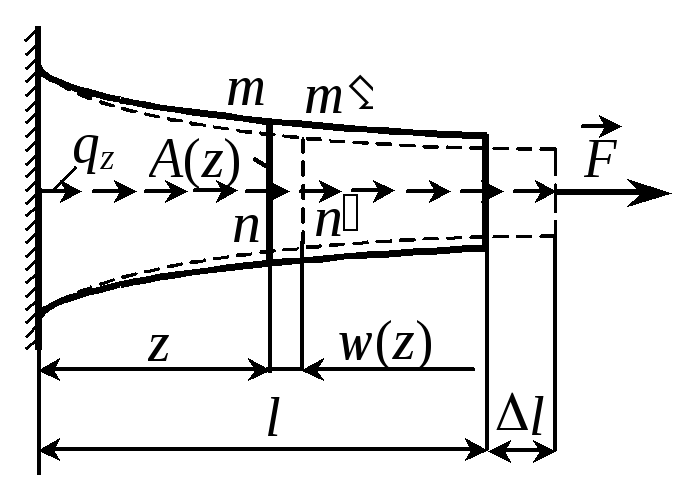
Рис. 2.4

где Е – модуль продольной упругости или модуль Юнга. Удлинение или укорочение стержня в общем случае (рис. 2.4) определяется интегралом . (2.5)

В частном случае, когда N_z = F = const и EA = const (рис. 2.3),

l = N_zl / (EA). (2.6)

Величины ЕА и С = ЕА/l называются соответственно жесткостью сечения и жесткостью стержня при растяжении (сжатии).

Перемещение произвольного сечения z равно изменению длины участка, заключенного между этим сечением и заделкой (рис. 2.4), т.е.

, (2.7)

где _ - площадь эпюры  от защемления до рассматриваемого сечения.

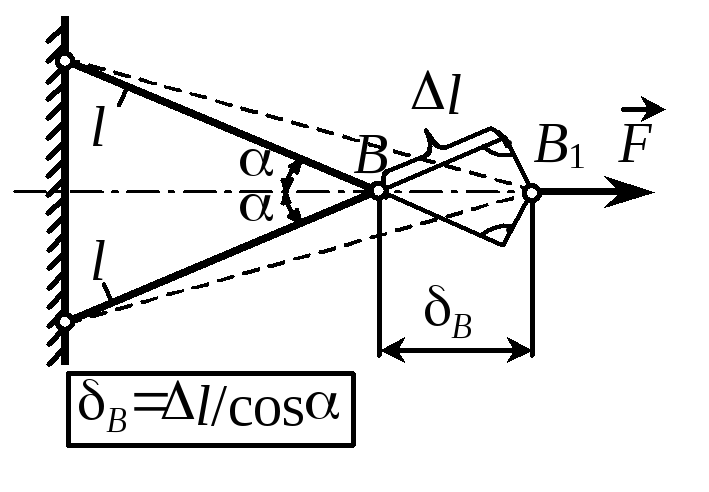
В стержневых системах перемещения узлов  определяются через деформации стержней (рис. 2.5). Условие жесткости    (2.8) позволяет решать задачи трех

Рис. 2.5

типов, аналогичных расчету на прочность, а именно: проверка жесткости, подбор сечений, определение допускаемой нагрузки.

При упругой деформации в единице объема стержня накапливается энергия (удельная потенциальная энергия)

u = ²/(2E). (2.9)

Энергия, накапливаемая во всем стержне

. (2.10)

Рис. 2.6

П р и м е р 2.1. Пространственный кронштейн, состоящий из трех стержней, нагружен силой F. Зная допускаемые напряжения материала стержней на растяжение р = 120 МПа и на сжатие сж = 60 МПа, требуется:

1) проверить прочность конструкции, если F = 120 кН, А₁ = А₂ = 4 см², А₃ = 25 см²;

2) подобрать сечения стержней из двух равнобоких уголков, если F = 480 кН;

3) определить, какой груз может выдержать кронштейн, если А₁ = А₂ = 10 см², А₃ = 60 см².

Р е ш е н и е. 1. Определение усилий в стержнях. Из условия равновесия узла С имеем:

X_i = 0, N₁sin - N₂sin = 0, N₁ = N₂;

Z_i = 0, N₃cos - F = 0, N₃ = F/cos = 1,25F;

Y_i = 0 2N₁cos = N₃sin, N₁ = N₃sin/(2cos) = 0,395F.

2. Определение искомых величин.

2.1. Проверка прочности конструкции

Находим напряжения в стержнях:

₁  ₂  N₁/A₁ = 0,39512010³/(410^-4) = 118,5 МПа_р = 120 МПа;

₃  N₃/A₃ = 1,2512010³/(2510^-4) = 60 МПа = _сж = 60 МПа.

Как видим, оба условия прочности выполняются, т.е. прочность конструкции в целом обеспечена.

2.2. П о д б о р с е ч е н и й

Из условия прочности на растяжение

,

откуда .

Из условия прочности на сжатие

,

откуда .

Принимаем по ГОСТ 8509-72 (СТ СЭВ 104-74):

- для 1-го и 2-го стержней – 2 уголка 70х70х6 (А₀₁ = 28,15 = 16,3 см²);

- для 3-го стержня – 2 уголка 160х160х16 (А₀₃ = 249,1 = 98,2 см²).

2.3. Определение допускаемой нагрузки

Из условия прочности на растяжение

,

откуда .

Из условия прочности на сжатие

,

откуда .

Допускаемая нагрузка равна меньшей из найденных величин, т.е.

F = min{[F_р], [F_сж]} = [F_сж] = 288 кН.

П р и м е р 2.2

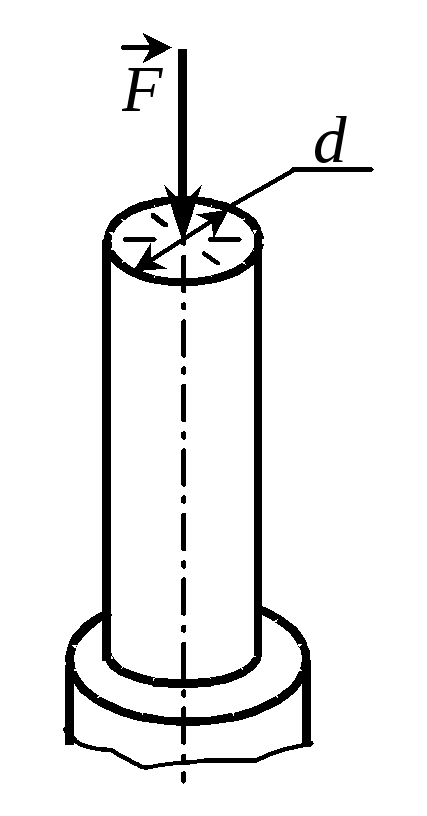
Круглая колонна диаметра d сжимается силой F. Определить увеличение диаметра d, зная модуль упругости Е и коэффициент Пуассона  материала колонны. Р е ш е н и е. Продольная деформация по закону Гука равна   z/E = -4F/(d2E).

Рис. 2.7

Используя закон Пуассона, находим поперечную деформацию     4F/(d²E).

С другой стороны,   d/d.

Следовательно, d = 4F/(dE).

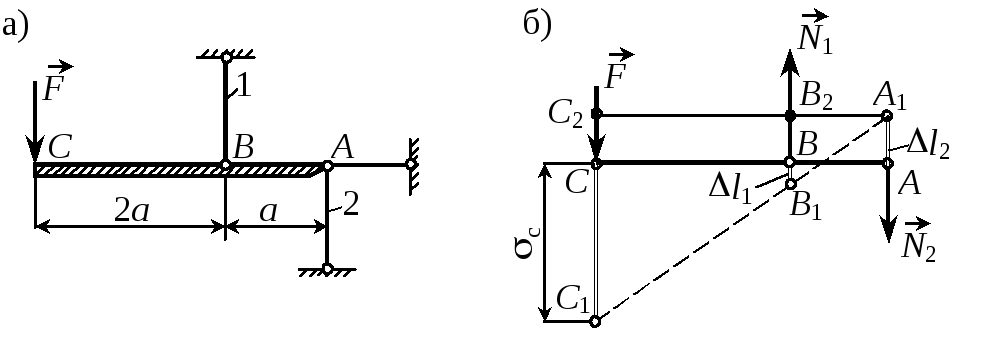
П р и м е р 2.3. Определить из расчетов на прочность и жесткость допускаемую силу F, если  = 120 МПа, _с = 1,7 мм, А₁ = 2А, А₂ = А = 5 см², l₁ = l₂ = l = 1 м, Е = 200 ГПа.

Рис. 2.8

Р е ш е н и е. 1. Определение усилий в стержнях. Из условия равновесия бруса АС имеем

m_A  , F3a - N₁a  , N₁  3F;

m_B  , F2a - N₂a  , N₂  2F.

2. Расчет на прочность. Находим напряжения в стержнях ₁  N₁/A₁ = 3F/(2A), ₂  N₂/A₂ = 2F/A.

Как видим, наиболее нагруженным является 2-й стержень, прочность которого предопределяет прочность всей конструкции в целом. Из условия прочности _max = ₂  2F/A находим F_m  0,5A  30 кН.

3. Расчет на жесткость. Вычисляем деформации стержней

l₁ = N₁l/(EA₁) = 3Fl/(2EA), l₂ = N₂l/(EA₂) = 2Fl/(2EA),

а по ним перемещение точки С. Из подобия треугольников В₁А₁В₂ и С₁А₁С₂ имеем: В₁В₂/А₁В₂ = С₁С₂/А₁С₂ или (l₁ + l₂)/a = (_C + l₂)/3a, откуда _C = 3l₁ + 2l₂ = = 9Fl/(2EA) + 4Fl/(EA) = 8,5Fl/(EA).

Записываем условие жесткости _C = 8,5Fl/(EA)  _C,

откуда F_ж = EA_C/(8,5l) = 20010⁹510^-41,710^-3/(8,51) = 20 кН.

Допускаемая нагрузка из расчета на жесткость получилась меньше, чем из расчета на прочность, поэтому ее и принимаем в качестве окончательной, т.е.

F = min{[F_m], F_ж} = F_ж = 20 кН.

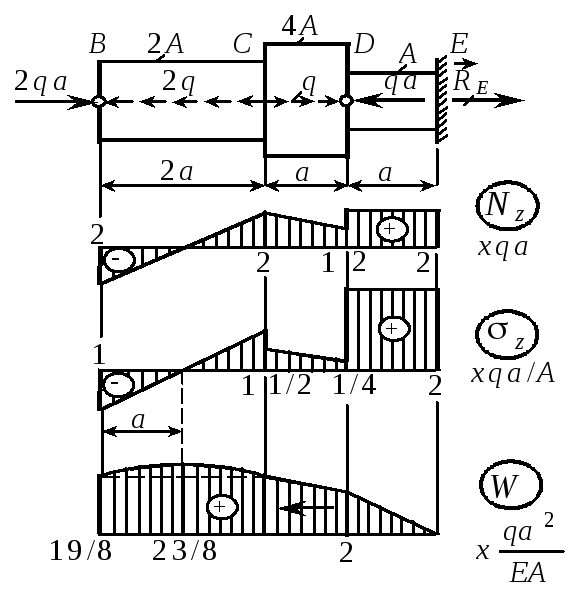
П р и м е р 2.4. Построить эпюры продольной силы, напряжения и перемещения для ступенчатого бруса. Р е ш е н и е. 1. Определение опорной реакции. Составляем уравнение равновесия в проекции на ось z: Zi = 0, -2qa + 2q2a- qa + qa-RE = 0, откуда RE = 2qa. 2. Построение эпюр Nz, z, W.

Рис. 2.9

Э п ю р а N_z. Она строится по формуле

N_z = N_oqz.

Имеем N_B = -2qa, N_C = N_B + 2q2a = 2qa

N_DC = N_C - qa = qa, N_DE = N_DC + qa = 2qa.

Э п ю р а _z. Напряжение равно _z = N_z/A(z). Как следует из этой формулы, скачки на эпюре _z будут обусловлены не только скачками N_z, но также резкими изменениями площади поперечных сечений. Определяем значения _z в характерных точках:

_B = N_B/(2A) = -2qa/(2A) = -qa/A,

_CB = N_C/(2A) = 2qa/(2A) = qa/A;

_CD = N_C/(4A) = 2qa/(4A) = qa/(2A), _DC = N_DC/(4A) = qa/(4A),

_DE = N_DE/A = 2qa/A и строим эпюру _z.

38