3.1.4. Метод Зейделя для систем линейных уравнений
Метод Зейделя
является модификацией метода простой
итерации. Вычисление
проводится по следующим формулам:
Достаточные условия сходимости итерационной последовательности приближенных решений системы и оценка погрешности проводятся по тем же формулам, что и в методе простой итерации.
Пример 3.2. Рассмотрим вычисление двух приближений по методу Зейделя для примера, решенного выше для метода простой итерации и оценим погрешность.
Вычисления будем проводить по формулам:
Выбираем начальное
приближение:
и получаем:
,
.
.
3.1.5 Метод Ньютона для систем нелинейных уравнений.
Пусть дана система:
Согласно методу Ньютона последовательные приближения вычисляются по формулам:
,
где
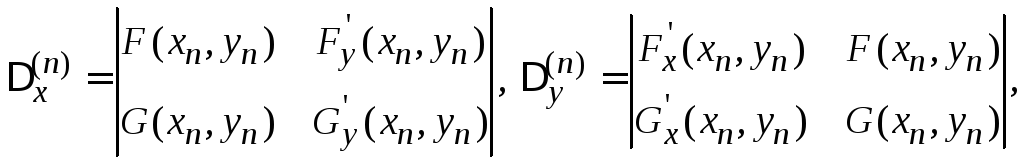
Начальные приближения
определяются приближенно (например,
графически).
Метод Ньютона эффективен только при достаточной близости начального приближения к решению системы.
Пример 3.3. Найти
одно приближение для решения системы.
За начальное приближение системы принять
.
.
Вычисляем в
начальной точке
:
.
Получаем первые приближения:
.
3.2. Лабораторная работа № 5 Решение систем линейных уравнений методом Гаусса. Вычисление обратной матрицы
Задания:
1) Решить заданную систему уравнений методом Гаусса с выбором главного элемента.
2) Вычислить для
матрицы Aобратную
матрицуA-1,
используя метод Гаусса. МатрицаA
задается системой уравнений
.
Варианты заданий к лабораторной работе № 5
№1 №2
№3 №4
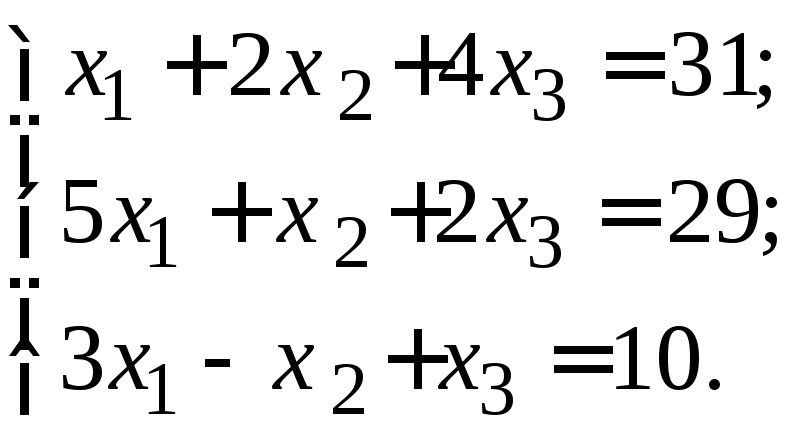
№3 №4
№5 №6
№7 №8
№9 №10
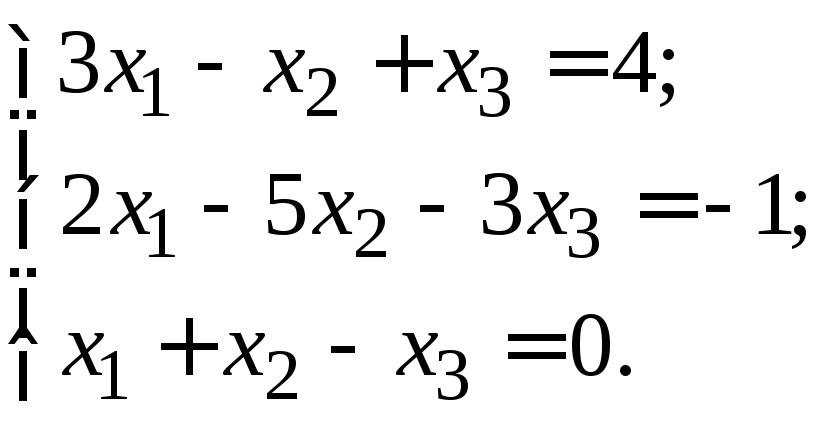
№11 №12
№13 №14
№15 №16
3.3. Лабораторная работа №6 Решение систем линейных уравнений методом простой итерации и методом Зейделя
Задания: Дана
система линейных уравнений
.
1) Привести систему линейных уравнений к итерационному виду.
2) Исследовать итерационную последовательность на сходимость.
3) Найти решение системы линейных уравнений методом простой итерации с точностью до = 0,00001.
4) Найти решение системы линейных уравнений методом Зейделя. с точностью до = 0,00001.
Варианты заданий к лабораторной работе № 6
№ 1.
,
.
№ 2.
,
.
№ 3.
,
.
№ 4.
,
.
№ 5 
,
.
№ 6.
,
.
№ 7.
,
.
№ 8. 
,
.
№ 9.
,
.
№ 10. 
, 
.
№ 11. 
, 
.
№ 12. 
, 
.
№ 13. 
, 
.
№ 14. 
, 
.
№ 15. 
, 
.
№ 16. 
, 
.
3.4. Лабораторная работа № 7 Решение систем нелинейных уравнений методом Ньютона
Задание:
Решить систему уравнений с помощью метода Ньютона. Результаты получить с пятью верными знаками. Начальные приближения найти графически.
Варианты заданий к лабораторной работе № 7
№ 1.
.
№ 2.
.
№ 3.
.
№ 4.
.
№ 5.
.
№ 6.
.
№ 7.
.
№ 8.
.
№ 9.
.
№ 10.
.
№ 11
№ 12
.
№ 13.
.
№ 13.
.
№ 14.
.
№ 15.
.
№ 16.
