Для студентов / (1)Векторы / 8Джерела векторного поля

Джерела векторного поля в ортогональних системах координат

Означення і смисл дивергенції векторного поля ()

Розглянемо поле , яке породжується скалярними джерелами, які ми будемо називати зарядами, розподіленими в деякій області неперервним чином. Нехай заряди заповнюють малу область, яка охоплює точку . Векторні лінії цього поля за межами області, зайнятій зарядами, розходяться в різні сторони. Кількість векторних ліній , у згоді з їх означенням, є пропорційною сумарному заряду області, який залежить як від густини розподілу зарядів, так і від об’єма області, зайнятої зарядами. Внаслідок цього бажано перейти від до такої характеристики векторних ліній, яка б залежала тільки від характеру розподілу зарядів.

Такою характеристикою є граничне значення відношення числа векторних ліній до величини об’єма , зайнятого зарядами. За означенням, вказане граничне значення прийнято називати дивергенцією векторного поля :

. (1)

З геометричної точки зору, є мірою розбіжності векторних ліній: чим більшою є густина заряду, тим більшим буде число векторних ліній, які розбігаються від фіксованої області, зайнятої зарядами.

З фізичної точки зору, є пропорційною густині зарядів, які породжують поле .

Спираючись на означення (1) дивергенції векторного поля , побудуємо формальний вираз, який зв’язує значення з похідними від вектора по координатам. Як перший крок, встановимо зв'язок між числом і потоком вектора через замкнуту поверхню , яка охоплює область, зайняту зарядами. За домовленістю, число векторних ліній, які перетинають площадку , перпендикулярну їх напрямку, дорівнює . Якщо напрямок вектора не є перпендикулярним до площадки , то число векторних ліній, які її перетинають, дорівнює , де - одиничний вектор, перпендикулярний до площадки. Повне число векторних ліній, які перетинають замкнуту поверхню , дорівнює: . В переважній більшості фізичних ситуацій є важливим не тільки число силових ліній, а й те, входять вони всередину об’єма, обмеженого замкнутою поверхнею , чи виходять з нього. Для врахування цієї обставини, будемо вважати, що в кожній точці поверхні одиничний вектор є направленим зовні обмеженого поверхнею об’єма. Тоді, число векторник ліній, які виходять з області, зайнятій зарядами, або входять до неї, можно обчислити за формулою:

. (2)

Величину прийнято називати потоком вектора через замкнуту поверхню .

Якщо проекція вектора на напрямок є позитивною, векторні лінії виходять зовні. В протилежному випадку – входять всередину об’єму. Підкреслимо, що напрямок векторних ліній визначається знаком зарядів.

Комбінуючи (2) і (1) для знаходимо остаточну загальну формулу:

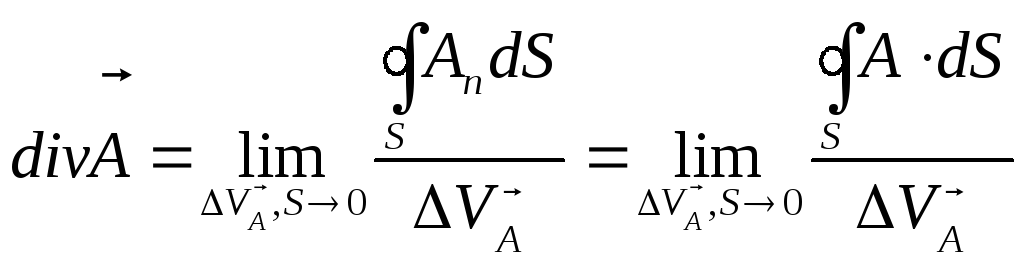, (3)

де враховано, що .

Для знаходження диференціального виразу для скористаємось довільною тривимірною криволінійною системою координат (). Об’єм візьмемо у формі куба, три ребра якого співпадають з відповідними відрізками осей координат, а точка їх перетинання має координати (). Зважаючи на малі розміри куба, потік вектора через поверхню куба можна апроксимувати наступним чином:

=.

Оскільки , і , а коефіцієнти Ламе в загальному випадку є функціями координат , , то вираз для потоку вектора через замкнуту поверхню можна спростити і далі, розкладаючи вирази в ряд Тейлора за малою величиною . У такий спосіб отримуємо:

.

Елемент об’єму в криволінійних ортогональних координатах дорівнює:

.

Підставляючи ці вирази в (3), знаходимо:

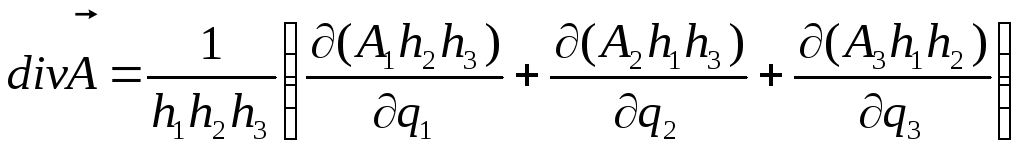. (4)

В ДСК () формула (4) переходить в

. (5)

Похідну , а також всі інші похідні, можна представити як , де - -а компонента векторного оператора набла (). Завдяки цьому (5) переходить у скалярний добуток оператора набла і вектора :

. (7)

Означення і смисл ротора векторного поля ()

Для того, щоб зрозуміти мотиви введення і точний смисл , розглянемо наочний приклад, в якому поле асоціюється з полем швидкостей рідини, утвореним внаслідок обертання ємності з рідиною. Будемо розглядати випадок повністю усталеного руху, коли рідина є нерухомою відносно стінок ємності, але обертається разом з ємністю відносно лабораторної системи координат (ЛСК). Нехай ємність має циліндричну форму і обертається навколо осі симетрії, якій будемо співставляти вісь ДСК.

Очевидно, що головною характеристикою такого обертального руху рідини є кутова швидкість обертання ємності. Поставимо питання, чи можна і яким чином кутову швидкість виразити через характеристики поля швидкостей в ЛСК?

Для розв’язання цієї задачі будемо виходити з того, що швидкість рідини відносно ЛСК описується формулою:

. (1)

Приріст вектора швидкості рідини, який відповідає зміщенню точки , дорівнює:

, (2)

і проектується на осі координат наступним чином:

, , . (3)

Звідси і випливає розв’язок поставленої задачі. Кутова швидкість рідини виражається через похідні по координатам від компонент вектора швидкості:

. (4)

Кутовій швидкості можна надати і більш симетричний вигляд:

. (5)

Формула (5) повністю розв’язує поставлену задачу у випадку усталеного вісе-симетричного руху рідини.

Вона легко узагальнюється і у тому випадку, коли рух рідини залишається вісе-симетричним, але не є усталеним. В цьому випадку формула (1) вже не працює, але швидкість рідини в циліндричній області, яка безпосередньо прилягає до довільної вісі, направленої паралельно вісі , може бути записаною наступним чином:

. (6)

Покладаючи , ми можемо встановити зв'язок між і похідними вектора швидкості тим самим способом, що і вище:

. (7)

Якщо рідина обертається навколо осей або , структура формули (5) залишається незмінною. Неважко впевнитись, що

, (8)

. (9)

Довільний рух рідини, фактично, є суперпозицією обертань навколо осей ().

Тому вектор кутової швидкості можна представити у вигляді:

,

або

. (10)

Введемо за означенням вектор , ротор поля швидкостей, який дорівнює подвоєній кутовій швидкості обертання рідини:

. (11)

У згоді з цим можна говорити, що ротор векторного поля швидкостей рідини є мірою завихрення його векторних ліній

Оскільки векторним лініям довільного векторного поля можна завжди поставити у відповідність векторні лінії гідродинамічного поля швидкостей, то стає цілком зрозумілим, що має той самий смисл міри завихрення його векторних ліній. Розрахунок виконується цілком аналогічним чином. У згоді з (10) і (11):

. (12)

Записуючи похідну у вигляді , де - -а компонента векторного оператора набла (), формулі (12) можна надати наступний вигляд:

.

Інтегральне представлення

Як і в попередньому підрозділі, розглянемо спочатку можливість інтегрального представлення ротора поля швидкостей рідини. Виходимо з того, що поле швидкостей рідини, рух якої зводиться тільки до обертання, в безпосередньому околі точки має вигляд (6).

Одначе, для знаходження кутової швидкості ми скористаємось іншим засобом. Обчислимо циркуляцію вектора швидкості рідини вздовж довільного необмежено малого контура , який охоплює вісь обертання:

. (13)

Як завжди, обхід контура виконується проти часової стрілки. Для замкнутого контура . Далі, виконаємо циклічну перестановку векторів і скористаємось тим, що дорівнює подвоєній площі трикутника, побудованого на векторах і як на сторонах. Тоді,

, (14)

де - одиничний вектор, перпендикулярний площині, в якій лежить необмежено малий контур , а - його площа. З (13) і (14), таким чином, випливає, що

.

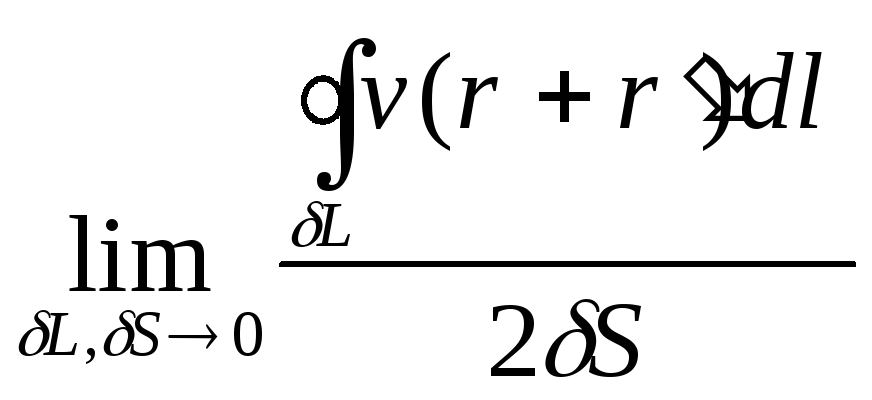Спираючись на цю формулу і (11), можна написати:

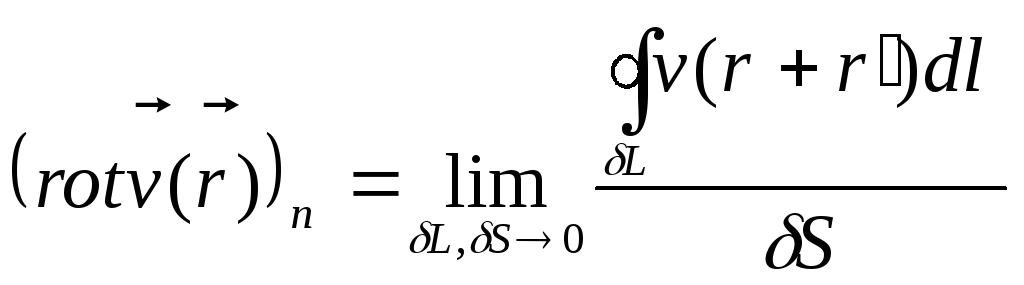. (15)

Це і є очікуване інтегральне представлення ротора швидкості рідини. Завдяки існуванню відповідності між довільним полем і полем швидкостей рідини, формула (15) тривіальним чином узагальнюється:

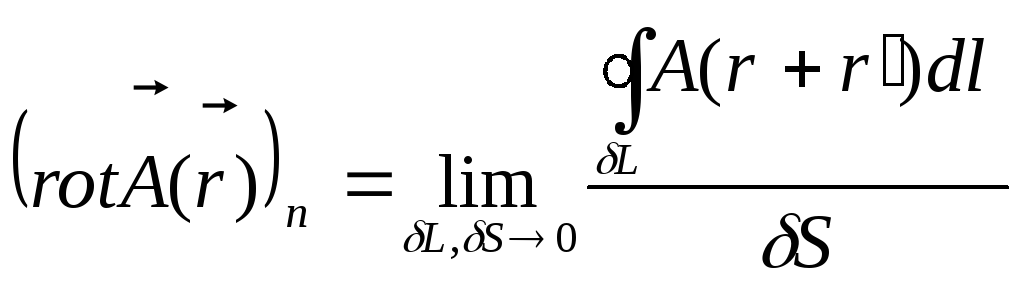. (16)

Треба відзначити, що формула (16) є особливо корисною при побудові явних виразів для компонентів в криволінійних ортогональних системах координат, прикладом яких може служити сферична система координат.

Обчислення в криволінійних ортогональних координатах

Нехай контур лежить в площині, перпендикулярній вісі тривимірної криволінійної системи координат, і має форму квадрата, дві сторони якого лежать осях координат, а дві інші є паралельні їм. Оскільки сторони цього квадрата малі, циркуляційний інтеграл можна апроксимувати алгебраїчною сумою:

. (17)

У згоді з означенням коефіцієнтів Ламе:

, , .

В загальному випадку коефіцієнти Ламе є функціями координат: , тому

. (18)

Підставляючи (17), (18) і в (16), отримуємо:

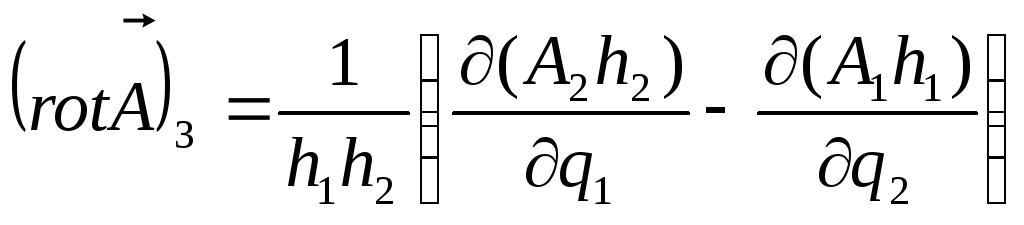. (19)

У такий самий спосіб знаходимо і дві інші компоненти :

,

.

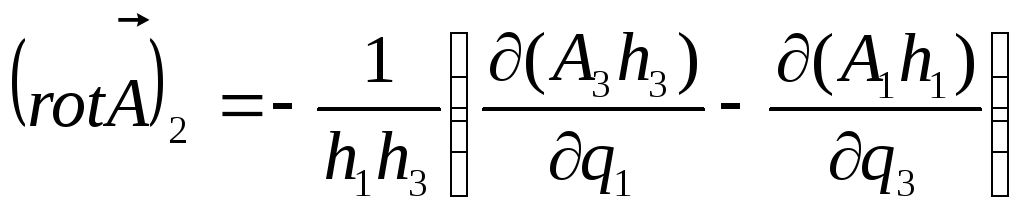Неважко впевнитись, що виписані компоненти вектора відповідають детермінанту:

. (20)

В найпростішому випадку ДСК ()

. (21)

Відомо, що значення неперервної скалярної функції однієї змінної в двох близьких точках і пов’язані між собою формулою Тейлора:

,

де позначає похідну го порядку. Якщо , то в нескінченому ряду можна обмежитись тільки першими двома внесками:

, (1)

де позначає необмежено малий приріст аргумента функції, тобто його диференціал.

Якісно формула (1) означає, що для визначення значення функції в необмежено близькій точці потрібно знати значення самої функції та її першої похідної в точці .

Розглянемо з таких же позицій зв'язок між значеннями векторного поля у двох сусідніх точках: () і (). Для визначеності розглянемо -у компоненту вектора . Очевидно, що аналогом (1) буде співвідношення:

, (2)

де по індексу , що повторюється, відбувається сумування в межах (1,3). Виконаємо кілька тотожніх перетворень:

1) від перейдемо до симетричної і антисиметричної комбінації похідних

;

2) в симетричній комбінації похідних виділимо ізотропну складову:

=,

і введемо позначення

. (3)

Від антисиметричної комбінації перейдемо до дуального вектора , який пов'язаний з нею співвідношенням:

, (4)

де - повністю антисиметричний тензор третього порядку.

Позначимо також

.

Тоді, формула (2) перепишеться у вигляді:

.

Повертаючись до векторних позначень, остаточно отримуємо:

, (5)

де вектор має компоненти: .

Таким чином, для визначення векторного поля в точках, сусідніх по відношенню до точки , необхідно, окрім значення функції в точці , додатково знати значення 1) скалярної функції , 2) векторної функції і 3) вектора , який породжується симетричною комбінацією похідних.

Для інтерпретації отриманого результату, розглянемо кілька характерних конфігурацій векторних полів в околі точки . Такими конфігураціями є:

а) поле, утворене множиною паралельних векторів: , де - одиничний вектор фіксованої орієнтації, - ;

б) плоско-паралельне поле , в якому при підходящому виборі ДСК, . Силові лінії цього поля є паралельними, вони лежать в площинах, паралельних осі і є протягнутими від до . Модулі векторів зростають пропорційно ;

в) поле, утворене сумою і полем , де , силові лінії якого починаються в точці і розподілені ізотропним чином навколо неї;

г) поле, утворене сумою і полем , силові лінії якого охоплюють точку .

В полі першого типу:

=0,

,

.