
termex / Theoretical_Mechanics_part_03_03
.pdf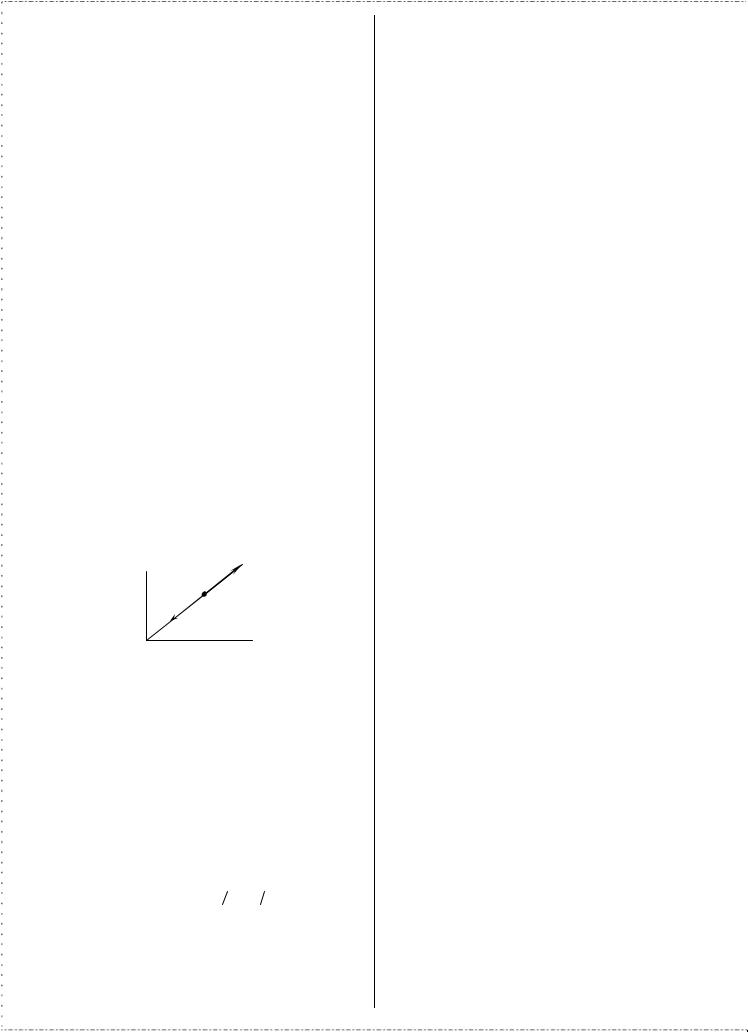
Динамика МТ |
Краткий курс Теоретической Механики |
54 |
§ 3. Прямолинейное движение материальной точки.
3.1. Условия прямолинейности движения.
Теорема: Для того чтобы движение свободной МТ
было прямолинейным, необходимо и достаточно, чтобы действующая сила имела постоянное направление, а начальная скорость точки была направлена вдоль линии действия этой силы или была равна нулю.
Пусть |
траектория МТ совпадает с осью Ox , |
тогда |
y = z = 0 |
и y& = z& = 0 , т.е. скорость точки во все |
время |
движения направлена по оси Ox , следовательно, и начальная скорость точки должна быть направлена по оси Ox или быть равной нулю.
Так как y&& = z&& = 0 , то из уравнений движения (1.4) следует, что Fy = Fz = 0 , т.е. что сила должна быть
направлена по оси Ox .
Таким образом, высказанные условия необходимы. Докажем их достаточность.
|
Пусть |
сила |
F |
направлена |
по оси |
Ox , тогда |
из |
||
уравнений |
движения имеем |
&& |
&& |
интегрируя |
их, |
||||
y = z = 0 и, |
|||||||||
получим: |
y& |
= c |
и z& |
= c . |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
Если |
начальная |
скорость |
направлена |
по оси Ox , |
то |
|||
c |
= c = 0 . Следовательно, |
y& = 0 и z& = 0 . |
|
||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
Интегрируя второй раз, получим y = c3 и z = c4 . |
|
|||||||
|
Если в начальный момент времени точка находилась на |
||||||||
оси Ox , |
то c3 = c4 = 0 и, y = 0 и z = 0 , т.е. траекторией |
||||||||
точки будет ось Ox .
Покажем теперь, что если сила – центральная и начальная скорость направлена по силе или равна нулю, то движение прямолинейно (см. Рис. 3.1).
y r M F
v0 x
O
Рис. 3.1
Возьмем за плоскость движения плоскость Oxy , и пусть
O будет центром силы F .
Так как по условию сила F – центральная, то будет иметь место закон площадей – момент количества движения или момент скорости относительно центра O есть величина постоянная, т.е. momO (v) = xy& − yx& = c .
Так как начальная скорость v0 проходит через центр сил
O (или равна нулю), то момент ее относительно того же центра O будет равен нулю, т.е. в начале движения точки имеем c = 0 .
Следовательно,
xy& − yx& = 0 , или y& y = x& x .
Интегрируя последнее уравнение, получаем:
ln y = ln x + ln c0 , или y = c0x ,
т.е. траекторией точки является прямая, проходящая через
r
центр силы F .
3.2. Дифференциальное уравнение прямолинейного движения.
Прямолинейное (вдоль оси Ox ) движение свободной материальной точки определяется одним дифференциальным уравнением второго порядка
mx = Fx |
(t, x,x) , |
(3.1) |
&& |
& |
|
r
где сила F может быть функцией времени t , координаты x данной точки и ее скорости x& . Интегрируя это уравнение, получим общее решение
x = x(t, c1, c2 ) . |
(3.2) |
Взяв производную по времени от выражения (3.2), будем иметь:
x& = x&(t,c ,c ) . |
(3.3) |
|
1 |
2 |
|
Для определения констант интегрирования c1 и c2 используем начальные условия движения: при t = t0 имеем x = x0 и x& = v0 . Тогда из (3.2) и (3.3) найдем
x0 = x(t0, c1, c2 ) и v0 = x&(t0, c1, c2 ) ,
подставив которые в (3.2), окончательно получим частное решение, соответствующее начальным условиям движения:
|
|
x = x(t,t0, x0,v0 ) . |
|
(3.4) |
|
Зависимость (3.4) является искомым законом |
|||||
прямолинейного движения материальной точки. |
|
||||
3.3. Общие теоремы динамики для прямолинейного |
|||||
|
|
|
|
|
движения. |
Уравнение (3.1), записанное в виде |
|
|
|||
m |
dvx |
= F |
или d(mv ) = F dt |
(3.5) |
|
|
|||||
|
dt |
x |
x |
x |
|
|
|
|
|
|
|
представляет собой частный случай теоремы об изменении количества движения МТ в дифференциальной форме.
Интегрируя уравнение (3.5) и полагая, что при t = 0 начальная скорость vx = v0x , находим выражение той же
теоремы в интегральной форме:
t |
|
mvx − mv0x = Sx, Sx = ∫Fxdt |
(3.6) |
0 |
|
|
r |
где Sx – есть проекция импульса равнодействующей F , приложенных к точке сил, на ось Ox .
r |
будет функцией только времени, т.е. |
Если сила F |
|
Fx = Fx (t) , или |
когда сила постоянна (Fx = const) , то |
импульс Sx непосредственно вычисляется и теорема (3.6)
дает первый интеграл уравнения движения. Если же преобразовать правую часть уравнения (3.1) к виду
|
dvx |
|
dvx dx |
|
|
dvx |
|
2 |
|
|
|
2 |
|
||||||
m |
= m |
= mv |
|
= |
m d(vx ) |
= |
d mvx |
|
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
dt |
dx dt |
x |
dx |
2 dx |
dx |
2 |
|||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то дифференциальное уравнение движения в форме:
|
|
2 |
|
|
2 |
|
|||
d mvx |
|
= F , откуда d |
mvx |
|
= F dx (3.7) |
||||
|
|
|
|
|
|
|
|||
dx |
2 |
2 |
|||||||
x |
x |
||||||||
|
|
|
|
|
|
|
|
|
|
© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ |
23 апреля 2007 г. |

Динамика МТ |
Краткий курс Теоретической Механики |
55 |
– будет выражать для прямолинейного движения теорему об изменении кинетической энергии в дифференциальной форме, а величина Fxdx будет в данном случае
элементарной работой равнодействующей сил F , приложенных к точке.
Интегрируя уравнение (3.7) и полагая, что при t = 0 скорость частицы есть vx = v0x , получим выражение
теоремы в интегральной форме
mv2 |
|
mv2 |
x1 |
x |
− |
0x |
= ΑM0 M1 , ΑM0 M1 = ∫Fxdx , (3.8) |
2 |
2 |
||
|
|
|
x0 |
где ΑM0 M1 – работа действующих сил на перемещении материальной частицы из положения M0 (x0 ) в положение M1(x1) на ее траектории.
В случае, когда сила зависит только от расстояния, т.е. Fx = Fx (x) , или постоянна (Fx = const) , работа ΑM0 M1
непосредственно вычисляется и теорема (3.8) дает первый интеграл уравнения движения (3.1).
Если сила постоянного направления зависит только от расстояния, то она будет потенциальной и в этом случае
элементарная |
работа |
есть |
|
Fx (x)dx = dU(x) , где |
||||||
потенциальная функция |
U(x) |
|
(потенциальная энергия |
|||||||
Π(x) ) есть U(x) = ∫Fx (x)dx + const = −Π(x) . |
||||||||||
Тогда теорема (3.8) примет вид: |
|
|
|
|||||||
|
mv2 |
mv2 |
|
|
|
|
|
|||
|
x |
− |
0x |
= U(x) −U(x |
0 |
) = Π(x |
0 |
) − Π(x) . |
||
2 |
2 |
|||||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
Покажем, что если сила есть функция только одного переменного, то дифференциальное уравнение прямолинейного движения интегрируется методом разделения переменных.
Случай 1. Пусть действующая сила – функция только времени:
Fx = Fx (t) .
Тогда теорема об изменении количества движения (3.6) сразу дает первый интеграл
|
|
|
|
|
|
t |
|
|
|
|
|
mvx − mv0x = ∫Fxdt , |
|||||||||
|
|
|
|
|
0 |
|
|
|
||
|
|
dx |
|
|
|
1 |
|
t |
|
|
откуда |
v = |
= v |
+ |
|
∫ |
F dt . |
||||
|
|
|||||||||
|
x |
dt |
0x |
|
m |
|
x |
|||
|
|
|
|
|
|
|
|
0 |
|
|
Интегрируя дальше, получим: |
|
|
|
|||||||
|
t |
|
|
1 |
t |
|
|
|
||
|
x(t) = ∫ v0x + |
∫Fxdt dt + x0 . |
||||||||
|
m |
|||||||||
|
0 |
|
|
0 |
|
|
|
|
||
Случай 2. Пусть действующая сила – функция только расстояния:
Fx = Fx (x) .
Тогда по теореме (3.8) будем иметь:
|
mv2 |
|
mv02 |
x |
|
||
|
− |
= |
∫ |
F dx = f(x) , |
|||
|
|
|
|||||
2 |
2 |
|
x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
или |
mv2 = mv2 |
+ 2 f(x) . |
|||||
|
|
|
|
|
0 |
|
|
Из этого уравнения, учитывая, что при прямолинейном движении vx = ±v , находим
v |
= dx = ± v2 |
+ 2 f(x) , |
|
x |
dt |
0 |
m |
|
|
||
где знак перед радикалом определяется по знаку vx . Разделив переменные, получим:
|
dt = |
|
|
|
dx |
. |
|
||||||
|
|
|
|
|
|
2 |
|
||||||
|
|
± |
v2 |
+ |
|
f(x) |
|
||||||
|
|
|
|
||||||||||
|
|
|
|
|
0 |
|
|
m |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегрируя последнее уравнение, получим |
x как |
||||||||||||
функцию времени, т.е. закон движения x = x(t) . |
|
||||||||||||
Случай 3. Пусть действующая сила – функция только |
|||||||||||||
скорости: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fx = Fx (vx ) . |
|
||||||||||
Тогда из уравнения |
|
|
|
|
|
|
|
|
|
||||
|
|
m |
dvx |
= F (v ) , |
|
||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
dt |
|
x |
|
x |
|
||||
|
|
|
|
|
|
|
|
|
|
||||
откуда |
|
m |
|
dvx |
|
= dt . |
|
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
Fx (vx ) |
|
|
|
||||||
Интегрируя, будем иметь |
|
|
|
|
|
|
|||||||
|
|
|
|
|
v |
|
|
|
|
|
|
||
|
t = t0 + m ∫x |
dvx |
|
= ϕ(vx ) . |
(3.10) |
||||||||
|
F (v ) |
|
|||||||||||
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
v0 |
|
|
|
|
|
|
||
Если |
из этого |
уравнения |
|
можно определить vx как |
|||||||||
функцию |
t , т.е. v |
= x& |
(t) = ψ(t) , то, интегрируя дальше, |
||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
||
найдем x(t) = ∫ψ(t)dt + c .
В противном случае можно применить другой способ интегрирования.
Представим ДУ движения в виде (3.7):
|
mv |
|
dvx |
= F (v |
|
) , |
||
|
|
|
|
|||||
|
|
|
x |
dx |
x |
x |
|
|
откуда |
|
mvxdvx |
= dx . |
|
||||
|
|
Fx (vx ) |
|
|||||
|
|
|
|
|
|
|||
После интегрирования последнего уравнения имеем
Φ(vx ) = x − x0 . |
(3.11) |
Исключая vx из уравнений (3.10) и (3.11), найдем искомый закон движения x = f(t).
© Составители: Асланов С.К., Царенко А.П., кафедра Теоретической Механики ОНУ |
23 апреля 2007 г. |
