Лабораторный практикум Физика / Часть_1 / 3_Обработка зависимостей

32

ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ЗАВИСИМОСТЕЙ

Соединить прямой две точки

Посредством каменной заточки

Легко сумеет папуас;

С тремя и более – не сладить

И всех погрешностей не сгладить,

Имея только верный глаз…

Определение коэффициентов линейной зависимости

Часто в практике физического эксперимента искомую величину невозможно определить из опытов, проведенных в одних и тех же условиях. Например, в лабораторной работе 1.3 требуется найти момент инерции J крестовины маятника Обербека. С этой целью измеряются момент М_н силы натяжения нити и угловое ускорение  крестовины. Связь между этими величинами устанавливает основной закон динамики вращательного движения, уравнение которого в данном случае имеет вид

, (15)

где М_тр – момент сил трения. Очевидно, что сколько бы опытов при одном и том же значении М_н ни проводилось, из формулы (15) нельзя найти момент инерции J, так как величина момента сил трения также неизвестна.

Введем обозначения:

,

с учетом которых выражение (15) приводится к стандартному виду линейной зависимости

, (16)

коэффициенты которой K и b неизвестны.

Формально для нахождения K и b достаточно измерить два значения функции y_I и y_II при различных значениях аргумента х_I и х_II. Подстановка этих значений в (16) позволяет получить систему двух независимых уравнений для определения неизвестных коэффициентов:

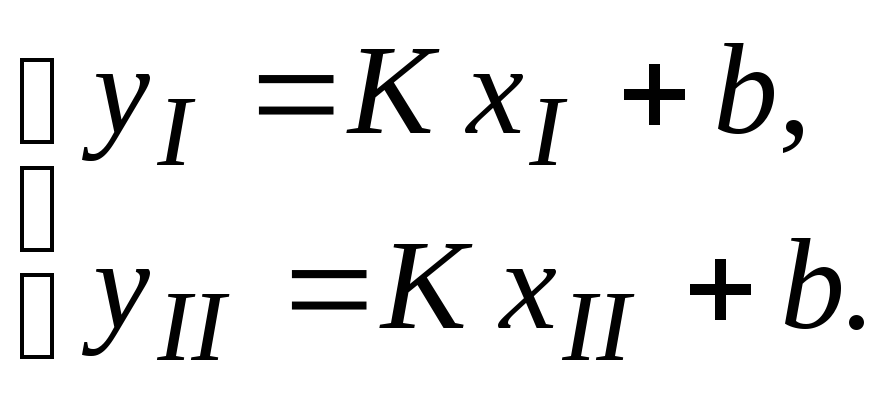
Решая систему, находим:

; (17)

.

Этот метод дает возможность получить лишь грубую оценку коэффициентов, так как величины х и у измеряются с погрешностями.

Учесть наличие погрешностей и найти некоторые осредненные значения K и b можно только путем неоднократного измерения величины у при различных х. В дальнейшем допустим, что в результате опытов получено п значений независимой переменной х₁, х₂,…, х_п и п соответствующих им значений функции у₁, у₂, …, у_п.

Графический способ

При использовании графического способа определения коэффициентов K и b экспериментальные точки наносят на график зависимости у(х), а затем проводят сглаживающую прямую (см. п. 7 правил построения графиков на с. 19). При условии, что ось абсцисс начинается с нуля, отрезок, отсекаемый этой прямой на оси 0у, численно – с учетом масштаба – равен коэффициенту b. Тангенс угла наклона прямой к оси 0х (опять же с учетом масштаба) дает значение коэффициента K. Для нахождения тангенса угла наклона нужно на сглаживающей прямой выбрать две точки I и II, расположенные достаточно далеко друг от друга и определить их координаты (значения аргумента х_I и х_II и функции у_I и у_II). Коэффициент K вычисляется по формуле (17), которую для краткости записывают в виде

,

где .

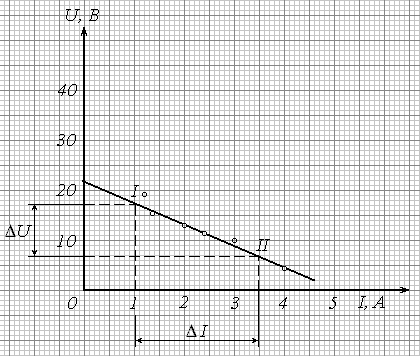
Пример 8. Для определения ЭДС аккумулятора E и его внутреннего сопротивления r были проведены измерения силы тока I в цепи источника и напряжения U на его зажимах при различной нагрузке. Экспериментальные результаты приведены в табл. 5.

Таблица 5

I, A	1,20	1,35	2,00	2,40	3,00	4,00
U, B	19,1	15,5	12,9	11,5	10,0	4,3

Теоретически, на основании закона Ома для замкнутой цепи, измеренные величины связаны соотношением

U = E  - I r. (18)

Сопоставляя с (16), имеем:

x  I ; y  U ; K = - r ; b = E . (19)

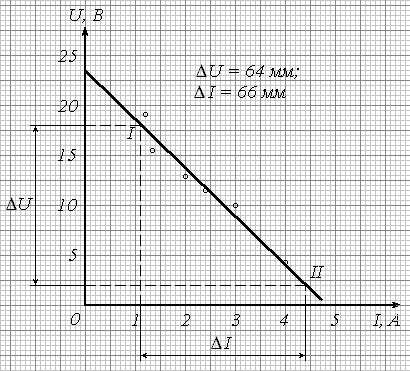
Построенный по данным табл. 5 график приведен на рис. 6. Обработка графической зависимости согласно вышеизложенным правилам дает следующие результаты:

E = b  23,5 (В);

.

Р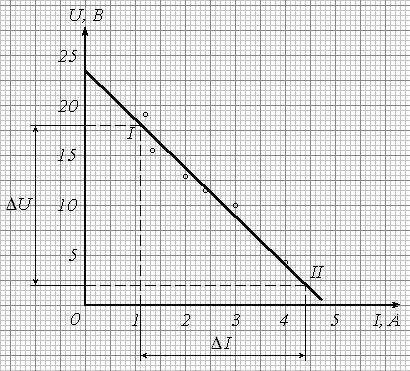 ис.6.

На рис. 7…12 показаны наиболее распространенные ошибки, допускаемые студентами при графической обработке линейных зависимостей.

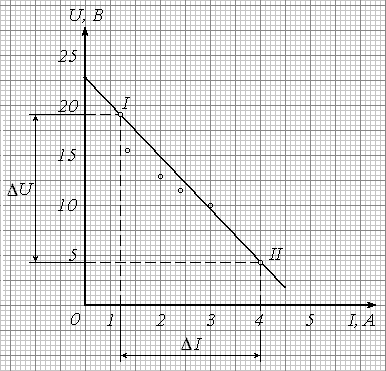
Рис.7. Рис.8.

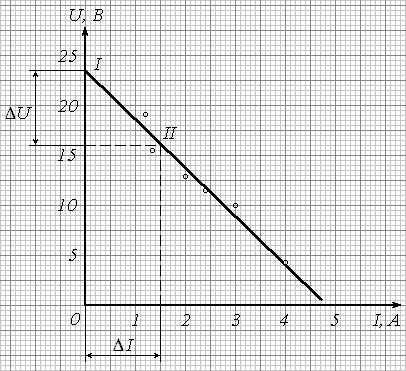
Рис. 7 иллюстрирует две типичные ошибки. Во-первых, неправильно определена величина E  = 22,5 В, т.к. ось абсцисс (токов) начинается не с нуля. Во-вторых, координаты точек I и II взяты не со сглаживающей прямой, а из таблицы экспериментальных данных – поэтому величина

–

не является осредненной, и случайная погрешность ее определения может быть очень большой (при таком способе вычисления r построение графика вообще не имеет смысла).

На рис. 8 точки I и II выбраны слишком близко друг к другу. При малых длинах отрезков U и I растет относительная ошибка их измерения, а следовательно, и погрешность определения углового коэффициента:

.

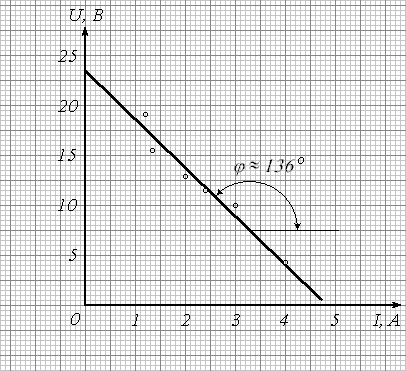
Рис.9. Рис.10

На рис. 9 и 10 графики построены безукоризненно, и величина E   = 23,5 В найдена верно. Тем не менее, здесь допущена, по сути дела, одна и та же грубейшая ошибка. Она заключается в том, что при определении тангенса угла наклона прямой не учтен масштаб откладываемых по осям переменных. В обоих случаях получим результаты

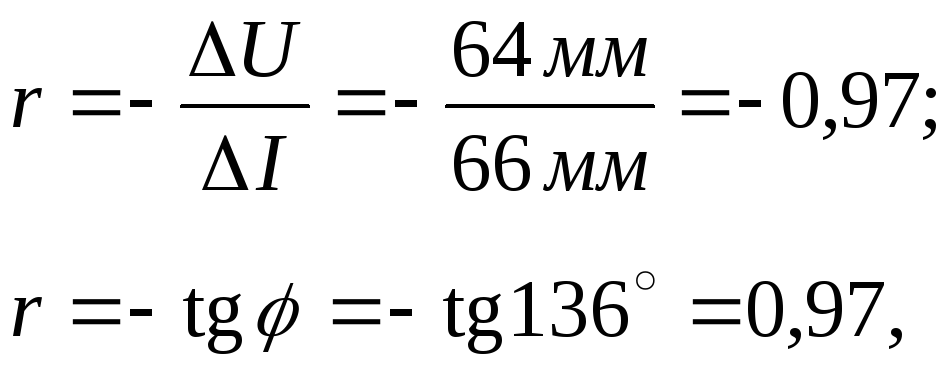
не имеющие ничего общего с искомой физической величиной и даже лишенные единиц измерения (только в том случае, когда отрезки U и I выражены, соответственно, в вольтах и амперах, их отношение будет иметь размерность Ом). Очевидно, что изменение масштаба графика приведет к изменению реального угла наклона прямой  , что при правильном определении углового коэффициента не должно влиять на п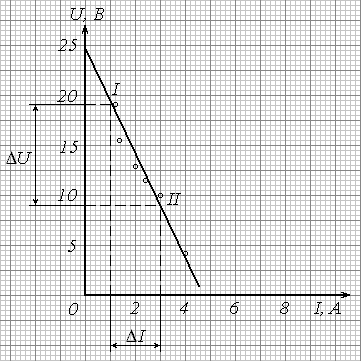 олучаемый результат.

Рис.11. Рис.12.

Ошибки, показанные на рис. 11 и 12, связаны с неудачным выбором масштаба (см. п. 6 правил построения графиков). Сжатие графика по оси ординат (рис.11) приводит к большой погрешности измерения величинE и U; последнее отрицательно влияет на точность определения r :

E = 21 B;

;

сжатие по оси абсцисс (рис.12) увеличивает ошибку измерения I и также приводит к снижению точности нахождения обоих коэффициентов:

E = 24,5 B;

.

Приведенные примеры свидетельствуют о том, что графический способ определения коэффициентов линейной зависимости не свободен от недостатков. Главный из них заключается в том, что проведение сглаживающей прямой носит субъективный характер. Это приводит к тому, что при значительном разбросе экспериментальных данных результат осреднения коэффициентов будет неоднозначным. Как показано на рис. 13, через одни и те же точки можно провести разные прямые – например, 1, 2 и 3, – и тем самым получить различные значения искомых коэффициентов. Причем в ряде случаев полученный результат может противоречить физическому смыслу. Например, если величина х представляет собой момент силы натяжения нити М_н , а у – угловое ускорение крестовины маятника Обербека (работа 1.3), то определенное по прямой 3 значение момента сил трения М_тр , в соответствии с формулами (15) и (16), будет отрицательным (при этом крестовина должна начать вращение в сторону, противоположную приложенному моменту силы натяжения).

Р ис.13.

Метод наименьших квадратов

Надежным и научно обоснованным способом определения коэффициентов экспериментальных зависимостей является метод наименьших квадратов. Суть его заключается в подборе таких значений коэффициентов, при которых сумма квадратов отклонений (СКО) измеренных в опытах значений y_i (i = 1, 2, …, n) от теоретических была минимальной.

Покажем, как подбираются значения коэффициентов K и b линейной зависимости у(х) вида (16). Найдем сумму квадратов отклонений

.

После раскрытия круглых скобок и возведения в квадрат получим

или

, (20)

где .

Из выражения (20) следует, что при различных значениях коэффициентов K и b величина S также будет принимать различные значения. Таким образом, СКО является функцией двух независимых переменных K и b. Для нахождения минимума функции S(K, b) необходимо приравнять к нулю ее частные производные:

Полученные выражения позволяют записать систему уравнений для отыскания «наилучших» значений коэффициентов K и b:

Решая эту систему, находим:

; (21)

, (22)

где

(23)

Обработку экспериментально полученных линейных зависимостей рекомендуется проводить в следующей последовательности:

1) для удобства выполнения расчетов составить таблицу (или дополнить таблицу экспериментальных данных) по образцу табл. 6;

Таблица 6

Номер опыта	…	Х	у	х 2	х у
1	…
2	…
…	…
п	…
	 =

2) измеренные (или рассчитанные с помощью измеренных величин) значения аргумента х и функции у занести в соответствующие столбцы таблицы;

3) для каждого i-го опыта (i = 1, 2, …, n) последовательно вычислить значения квадрата аргумента х_i² и произведения х_i y_i ; не округляя этих значений, занести их в два последних столбца таблицы;

4) рассчитать значения сумм S_x , S_y , S_xx , S_xy  и, не округляя, записать в соответствующие ячейки строки « = »;

5) по формулам (23), (21) и (22) вычислить значения коэффициентов линейной зависимости.

Пример 9. Используем метод наименьших квадратов для определения ЭДС аккумулятора E и его внутреннего сопротивления r (пример 8 на с. 23). Занесем данные табл. 5 во второй и третий столбцы табл. 7.

Таблица 7

Номер опыта	I, A	U, B	I 2, A2	IU, AB
1	1,20	19,1	1,4400	22,920
2	1,35	15,5	1,8225	20,925
3	2,00	12,9	4,0000	25,800
4	2,40	11,5	5,7600	27,600
5	3,00	10,0	9,0000	30,000
6	4,00	4,3	16,0000	17,200
 =	13,95	73,3	38,0225	144,445

Вычисляя значения I ² и IU (без округления), заполним последние два столбца таблицы. Сложим числа по столбцам и занесем результаты в строку « = ».

Учитывая соотношения (19), с помощью формул (23), (21) и (22) найдем ЭДС и внутреннее сопротивление аккумулятора:

E =

Линеаризация нелинейных зависимостей

Описанный выше графический способ, а также полученные методом наименьших квадратов формулы (21)-(23) для расчета коэффициентов в ряде случаев могут быть использованы и при обработке нелинейных зависимостей. В первую очередь это относится к зависимостям, описываемым степенными и показательными (экспоненциальными) функциями. Для их линеаризации (приведения к линейному виду) применяется операция логарифмирования.

Степенная зависимость. Пусть измеряемые величины Х и Y теоретически связаны зависимостью вида

Y = CX ^k,

где С и k – неизвестные коэффициенты. Логарифмируя данное выражение, получим

Приняв обозначения

придем к зависимости вида (16). После определения коэффициентов K и b одним из описанных выше способов, найдем параметры исходной зависимости:

Экспоненциальная зависимость. Многие физические явления и процессы (движение тела в вязкой среде, затухающие колебания, радтоактивный распад, поглощение излучения веществом и др.) описываются дифференциальными уравнениями, решение которых приводит к экспоненциальной (показательной) зависимости между физическими величинами х и Y :

Y = Сexp(K x). (24)

Если коэффициенты А и K неизвестны, но имеется экспериментально полученная зависимость Y(x), то для определения С и K ее приводят к линейному виду путем логарифмирования:

.

Положив , опять придем к зависимости вида (16), коэффициенты которой K и b можно найти как графическим способом, так и методом наименьших квадратов. После этого предэкспоненциальный множитель, т.е. коэффициент С исходной зависимости (24), определится как

С = ехр(b).

Пример 10. Зависимость сопротивления R полупроводника от его абсолютной температуры Т (лабораторная работа 6.2) имеет вид

, (25)

где R_ – константа, характеризующая сопротивление данного полу- проводника при бесконечно высокой температуре; W – энергия активации; k – постоянная Больцмана. Путем замены переменных

и введения обозначений

,

после логарифмирования выражения (25) придем к линейной зависимости (16). Измеряя сопротивление R при различной температуре Т, одним из описанных выше способов можно найти коэффициенты K и b, а затем перейти к параметрам исходной зависимости:

.

Пример 11. При изучении явления термоэлектронной эмиссии с помощью вакуумного (лампового) диода получена зависимость плотности тока насыщения j_н от температуры катода Т. Теоретически связь между этими величинами устанавливает закон Ричардсона-Дэшмена

, (26)

где С – постоянный множитель; е – элементарный заряд;  – потенциал выхода; k – постоянная Больцмана.

Для линеаризации выражения (26) разделим обе его части на Т ² и прологарифмируем, в результате чего получим линейную зависимость вида (16) с переменными

и коэффициентами

.

После определения коэффициентов K и b неизвестные параметры исходной зависимости (26) можно найти как

.

Пример 12. При изучении затухающих колебаний снималась зависимость их амплитуды А от числа колебаний N. Теоретически эти величины связаны экспоненциальным законом

, (27)

где А₀ – начальная амплитуда;  – логарифмический декремент затухания. Для определения неизвестных параметров А₀ и  зависимости (27) линеаризуем последнюю по аналогии с (24), логарифмируя ее

и вводя обозначения

.

Коэффициенты K и b линеаризованной зависимости будем искать методом наименьших квадратов. Составим табл. 8 по образцу табл.6; занесем в нее результаты измерений и соответствующих вычислений. Затем проведем расчеты по формулам (23), (21) и (22), учитывая принятые обозначения:

Таблица 8

Номер опыта	N	A, мм	ln A	N 2	Nln A
1	10	44	3,784	100	37,84
2	20	25	3,219	400	64,38
3	30	16	2,773	900	83,19
4	40	10	2,303	1600	92,12
 =	100		12,079	3000	277,53

Параметры исходной зависимости (27):

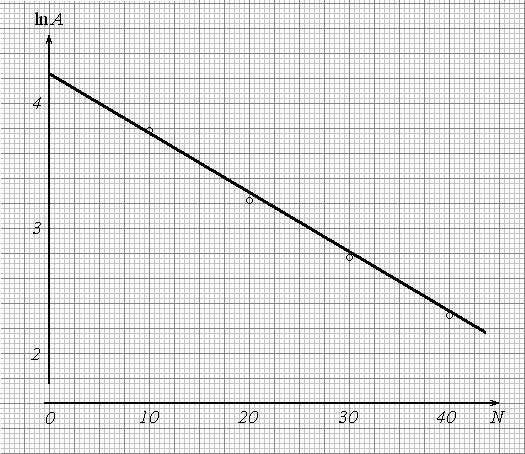
На рис. 14 для наглядности изображены графики исходной (а) и линеаризованной (б) зависимостей амплитуды от числа колебаний. Кружками на графиках обозначены экспериментальные данные, сплошными линиями – результаты расчетов по найденным значениям параметров А₀ и .

а б

Рис.14.