2.Применение метода симметричных составляющих для расчета коротких замыканий и обрывов фаз.

При появлении несимметрии в электрической сети нарушается симметрия токов в фазах, фазных и линейных напряжений, падений напряжений в элемен­тах системы и других электромагнитных величин. Из этого следует, что при не­симметричном коротком замыкании или (и) появлении продольной несиммет­рии нельзя ограничиваться расчетом только одной фазы, как это делается при исследовании трехфазного короткого замыкания. Если при этом исходить из обычного метода расчета, потребовалось бы составить схему замещения для всех трех фаз рассматриваемой сети с учетом взаимоиндукции между ними. Полученная при этом система управлений весьма сложна, так что такой метод решения задачи громоздок даже в случае простой схемы.

Сравнительно просто несимметричные короткие замыкания и другие не­симметричные режимы можно рассчитывать с использованием метода симмет­ричных составляющих.

Любую несимметричную систему трех векторов можно разложить на три симметричные схемы: прямой, обратной и нулевой последовательности (рис.6.1).

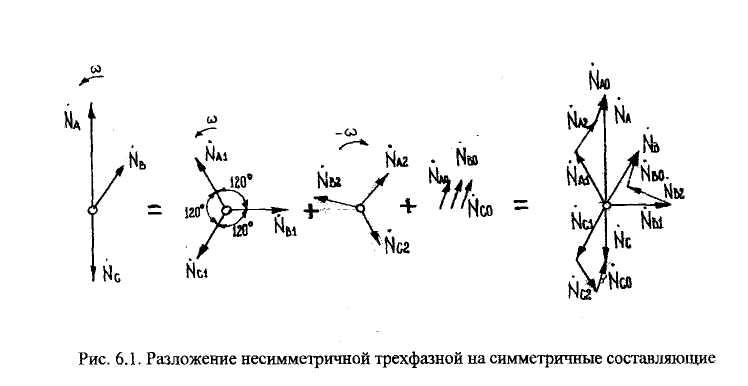
Система прямой последовательности состоит из трех одинаковых векто­ров, сдвинутых относительно друг друга на 120° и чередующихся в такой же последовательности, как и исходная система. Система обратной последователь­ности также состоит из трех одинаковых векторов, сдвинутых друг относитель­но друга на 120°, но чередование этих векторов противоположно чередованию исходной системы. Система нулевой последовательности состоит их трех оди­наковых векторов, совпадающих по направлению.

В симметричной трехфазной системе каждый вектор можно представить:

N_A = a N_B = a² N,

N_B = aN_c = a²N,

N_c = a N_A= a² N , где а - оператор поворота; a = e^j120 =-1/2+j√3/2.

По определению, приняв фазу «А» за особую (исходную) фазу, можно за­писать

N_A = N_A1 + N_A2 + N_ao,

N_b = N_B1 + N_B2 + N_A1 = a² N_A1 + a N_A2 + N_A0,

N_c =N_C1+ N_C2 + Nco= aN_A1 +a²N_A2 + N_A0 .

Строгий математический анализ несимметричных переходных процессов существенно затруднен тем, что в синхронных машинах при этом образуется пульсирующее магнитное поле ротора, которое имеет полный спектр высших гармоник. Системы токов прямой и обратной последовательности разных час­тот при этом оказываются взаимно связанными. Поэтому для изменения метода симметричных составляющих делаются допущения:

в симметричных цепях ток и напряжение разных последовательностей не взаимодействуют друг с другом;

каждый элемент цепи оказывает свое специфическое сопротивление токам разных последовательностей.

Следовательно, симметричные составляющие падения напряжения на не­котором элементе:

∆U₁ = z₁I₁, ∆U₂ = z₂I₂, ∆U₀ = z₀I₀

где z₁, z₂, z₀ - соответственно сопротивления прямой, обратной и нулевой по­следовательности.

ЭДС симметричного источника питания, например синхронного генерато­ра, образует основную симметричную систему векторов. При симметричном коротком замыкании такая система ЭДС вызывает в контуре только токи пря­мой последовательности.

При нарушении в системе симметрии возникают несимметричные напря­жения, связанные с появлением несимметричной системы токов.

Токи обратной и нулевой последовательностей образуют в генераторе со­ответствующие магнитные потоки, которые сцепляясь с его обмотками в свою очередь вызывают соответствующие ЭДС. Последние можно учитывать паде­нием напряжения в реактивном сопротивлении генератора той или иной последовательности, аналогично тому, как ЭДС реакции статора генератора учиты­вается падением напряжения в соответствующем реактивном сопротивлении.

Иначе говоря, можно считать, что при любом режиме генератор вырабаты­вает ЭДС только прямой последовательности, а ЭДС обратной и нулевой по­следовательностей равны нулю. Таким образом, несимметричные режимы в системе можно рассчитывать по эквивалентным однолинейным схемам заме­щения прямой, обратной и нулевой последовательностей (рис.6.1), полагая, что протекающие токи в схемах замещения различных последовательностей зави­сят лишь от действующей в схеме разности потенциалов и сопротивления соот­ветствующей последовательности.

Уравнение для каждой последовательности име­ет вид:

U_A1 = E_∑ - z_1∑ I₁,

U_A2 = 0 – z_2∑ I₂

U_A0 = 0 – z_0∑ I₀

где U_A1, U_A2, U_A0, I₁, I₂, I₀ - симметричные составляющие напряжения и тока в месте короткого замыкания (поперечная несимметрия) или обрыва фаз (про­дольная несимметрия),

E_∑- результирующая ЭДС;

Z_1∑, z_2∑, z_0∑ - результирующие сопротивления прямой, обратной и нулевой последовательностей относительно точки короткого замыкания или места об­рыва фазы.