госы / Шпоры - 5

7.4. Классификация форм самостоятельной деятельности учащихся при обучении математике

Самостоятельная работа – это такая работа, которая выполняется без непосредственного участия учителя, но по его заданию, в специально предоставленное для этого время, при этом учащиеся, сознательно стремятся достигнуть поставленные цели, употребляя свои усилия и выражая в той или иной форме результат умственных или физических (либо тех и других вместе) действий.

Самостоятельная работа представляется как целенаправленная, внутренне мотивированная структурированная самим объектом в совокупности выполняемых действий и корригируемая им по процессу и результату деятельности. Её выполнение требует достаточно высокого уровня самосознания, рефлективности, самодисциплины, личной ответственности, доставляет ученику удовлетворение как процесс самосовершенствования и самопознания. Во-первых, в данном определении принимаются во внимание психологические детерминанты самостоятельной работы.

«Самостоятельность» – очень многоаспектный и психологически непростой феномен, это скорее смыслообразующая, качественная характеристика, какой- либо сферы деятельности и личности, имеющая собственные конкретные критерии.

«Самодеятельность» – субъективная, собственно индивидуальная самоуправляемая деятельность, с личностно обусловленными компонентами: целью, ведущей потребностью, мотивацией и способами реализации.

«Самоактивация» – это субъективно соотнесённая внутренняя мотивация деятельности.

«Самоорганизация» – свойство личности мобилизовать себя, целеустремлённо, активно использовать все свои возможности для достижения промежуточных и конечных целей, рационально используя при этом время, силы, средства.

«Саморегуляция» – изначально психологическое обеспечение деятельности, в последующем развитии приобретающее личностный смысл, т.е. собственно психическое наполнение.

«Самоконтроль» – необходимый компонент самой деятельности, который осуществляет её исполнение на личностном уровне. Во-вторых, акцентируется внимание на том, что самостоятельная работа связана с работой школьника в классе и является следствием правильной организации учебно-познавательной деятельности на уроке. В-третьих, самостоятельная работа рассматривается как высший тип учебной деятельности, требующий от учащегося достаточно высокого уровня самосознания, рефлексивности, самодисциплины, ответственности, и доставляющий ученику удовлетворение, как процесс самосовершенствования и самосознания.

Эффективность учебного процесса познания определяется качеством преподавания и самостоятельной познавательной деятельностью учеников. Эти два понятия очень тесно связаны, но следует выделить самостоятельную работу как ведущую и активизирующую форму обучения в связи с рядом обстоятельств.

Самостоятельная работа представляет собой, с одной стороны, учебное задание, т.е. то, что должен выполнить ученик, объект его деятельности, с другой – форму проявления соответствующей деятельности: память, мышление, творческого воображения при выполнении учеником учебного задания, которое, в конечном счете, приводит ученика либо к получению своевременно нового,заранее неизвестного ему задания, либо к углублению и расширению сферы действий уже полученных знаний. Следовательно, самостоятельная работа – это такое средство обучения, которое:

• в каждой конкретной ситуации усвоения соответствует конкретной дидактической цели и задаче;

• формирует у учащихся на каждом этапе его движения от незнания к знанию необходимые объём и уровень знаний, умений и навыков.

• вырабатывает у учащихся психологическую установку на самостоятельное систематическое пополнение своих знаний и выработку умений ориентироваться в потоке научной и общественной информации при решении новых познавательных задач;

• является важнейшим орудием педагогического руководства и управления самостоятельной познавательной деятельности учащихсяв процессе обучения.

Виды самостоятельной работы:

1. Работа с книгой.

При данном виде работы при изучении несложной новой темы в некоторых группах предлагается ученикам самостоятельно изучить часть нового материала, а затем объяснить его сильным учеником остальной группе.

2. Упражнения.

При выполнении типичных упражнений ученикам предлагается самостоятельно выполнить часть заданий, а затем осуществить взаимопроверку с соседом по парте при возникновении вопросов, разобрать пример на доске.

3. Выполнение практических работ.

На занятиях по геометрии предлагается в виде практической работы вычислить площади поверхности и объёмы многогранников, макеты которых выполнены самими учениками.

4. Проверочные самостоятельные, контрольные работы, математические диктанты.

5. Подготовка докладов, рефератов.

Учащимся предлагается выступить с докладами в научно-практической конференции, проводимой в училище каждый год.

6. Выполнение домашней работы.

Под самостоятельной работой обычно понимают работу, выполняемую без активной помощи «извне», когда выполняющий работу для достижения поставленной цели сам определяет последовательность своих действий, причины возникающих при этом затруднений и способы их устранения.

7.9. Методика обучения тождественным преобразованиям в курсе алгебры основной школы

Основные понятия. Числовые выражения составляются из чисел с помощью знаков действий и скобок. Число, которое получается в результате выполнения действий в числовом выражении, называют значением выражения. Выражение, составленное с помощью чисел, переменных и их степеней и знаков действий называется выражением с переменными. Если в выражении с переменными подставить вместо каждой переменной какое-либо её значение, то получится числовое выражение. Его значение называют значением выражения с переменными при выбранных значениях переменных. Два выражения называются тождественно равными, если при всех значениях входящих в них переменных, принадлежащих общей области определения, соответственные значения этих выражений равны.

Тождество —равенство, выполняющееся навсёммножествезначений входящих в негопеременных(равенство, верное при любых значениях переменных), например

,

.

Тождество обозначается «≡»

Тождественные преобразования выражений

Замену одного выражениядругим, тождественноравным ему выражениемназывают тождественным преобразованием или просто преобразованием выражения. Тождественные преобразования выражений с переменными выполняются на основе основных свойств действий над числами. Тождественное преобразование выражений широко применяются при вычислении значений выражений и решении других задач.

Некоторые тождественные преобразованиявам уже приходилось выполнять, например приведение подобных слагаемых и раскрытие скобок. Напомним правила выполнения этих преобразований:

• чтобы привести подобные слагаемые, нужно сложить их коэффициенты и результат умножить на общую буквенную часть;

• если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки;

• если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки.

Алгебраическим выражениемназывается одна или несколько алгебраических величин (чисел и букв), соединенных между собой знаками алгебраических действий: сложения, вычитания, умножения и деления, а также извлечения корня и возведения в целую степень (причём показатели корня и степени должны обязательно быть целыми числами) и знаками последовательности этих действий (обычно скобками различного вида).

Количество величин, входящих в алгебраическое выражение должно быть конечным. ТПВ с переменными – одна из основных задач элементарной алгебры, результаты решения которой служат средством изучения уравнений и неравенств, рационализации вычислений. Основными понятиями данной содержательно – методической линии являются понятия: «выражение», «тождественно равные выражения», «тождество» и «ТПВ». Выражением в математике называют запись, состоящую из чисел, букв (обозначающих постоянные или переменные величины), знаков математических действий. В числовых множествах имеют дело с числовыми выражениями.

Выражения делятся на алгебраические и неалгебраические (трансцендентные).

Те и другие могут быть, как целыми, так и дробными.

Алгебраические целые – это одночлены и многочлены первой, второй и высших степеней, а также, к алгебраическим относятся иррациональные выражения. К трансцендентным относятся тригонометрические, показательные и логарифмические.

Для каждого вида выражения существуют подвиды и простейшие (стандартные) виды.

Значения переменных, при которых выражение имеет смысл, называются допустимыми значениями переменных и образуют область определения выражения. Два выражения называются тождественно равными, если они принимают одинаковые числовые значения при подстановке соответственно равных числовых значений входящих в них букв из общей области определения.

Культура выполнения тождественных преобразований заключается в следующем:

1.Наличие прочных знаний, свойств, операций над выражениями и алгоритмов их выполнения.

2.Умение правильно обосновать преобразование.

3.Умение найти кратчайший путь перехода от исходного выражения к выражению наиболее соответствующего цели преобразования.

4.Умение проследить за изменением области определения выражения по цепочки их тождественных преобразований.

5.Быстрота и безошибочность выполнения преобразований.

Приёмы выполнений тождественных преобразований.

При выполнении тождественных преобразований алгебраических выражений необходимо знать порядок выполнения действий, действия с дробями и степенными выражениями, формулы сокращенного умножения и др.

Следует иметь в виду, что при тождественных преобразованиях остаются неизменными:

-величина допустимых изменений буквенных величин;

-область допустимых значений каждой из буквенных величин.

Первое из этих требований является обязательным при всех преобразованиях, имеющих целью упрощение выражения или приведение его к нужному виду. Если надо, например, дополнить квадратный трехчлендо полного квадрата,

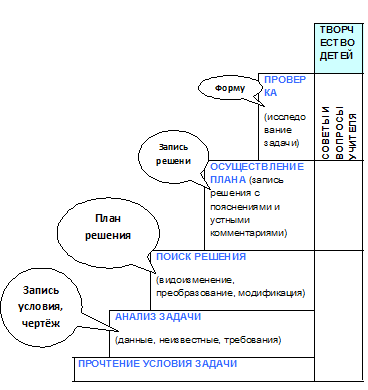
7.5. Задачи в обучении математике. Классификация задач

Задача представляет собой требование или вопрос, на который надо найти ответ, опираясь и учитывая те условия, которые указаны в задаче.

ФОРМУЛИРОВАНИЕ ОТВЕТА

Классификация. Проблеме классификации задач в современной методической и психологической литературе посвящено немало работ.

По характеру требования:

-задачи на доказательство;

- задачи на построение;

- задачи на вычисление.

По функциональному назначению (К.И. Нешков, А.Д. Семушин):

-задачи с дидактическими функциями;

- задачи с познавательными функциями;

- задачи с развивающими функциями.

По величине пробемности (У. Рейтман, Ю.М. Колягин):

-стандартные (известны все компоненты задачи);

- обучающие (неизвестен один из четырех компонентов задачи);

- поисковые (неизвестны два из четырех компонентов задачи);

- проблемные (неизвестны три из четырех компонентов задачи).

По методам решения задач:

задачи на геометрические преобразования,

задачи на векторы и др.

По числу объектов в условии задачи и связей между ними:

простые;

сложные.

По компонентам учебной деятельности:

организационно-действенные;

стимулирующие;

контрольно-оценочные.

Кроме того, различают задачи: стандартные и нестандартные; теоретические и практические; устные и письменные; одношаговые, двушаговые и др.; устные, полуустные, письменные и т.д.

Процесс решения задач

Решение задачи осуществляется в несколько этапов.

I. Ознакомление с содержанием задачи.

На первом этапе процесса решения задачи имеют место осознание условия и требования задачи, усвоение и разработка элементов условия (или элементов цели), поиск необходимой информации в сложной системе памяти, соотнесение условия и заключения задачи с имеющимися знаниями и опытом и т.д.

II. Поиск решения - выдвижение плана решения задачи.

На втором этапе происходят целенаправленные пробы различных сочетаний из данных и искомых, попытки подвести задачу под известный тип, выбор наиболее приемлемого в данных условиях метода решения (из известных), выбор стратегии решения, поиск плана решения и его корректировка на основе предварительной апробации, соотнесения с условием задачи и интуитивных соображений, фиксирование определенного плана решения задачи и т.д.

III. Процесс решения - реализация плана решения.

На третьем этапе проводится практическая реализация плана решения во всех его деталях с одновременной корректировкой через соотнесение с условием и выбранным базисом, выбор способа оформления решения, запись результата и т.д.

IV. Проверка решения задачи.

На четвертом этапе фиксируется конечный результат решения, проводится критический анализ результата, поиск путей рационализации решения, исследование особых и частных случаев, выявление существенного (потенциально полезного), систематизация новых знаний и опыта и т.д.

Сюжетной задачейназывают такую задачу, в которой данные и связь между ними включены в фабулу. Содержание сюжетной задачи чаще всего представляет собой некоторую ситуацию, более или менее близкую к жизни. При решении текстовой задачи с помощью составления уравнения необходимо придерживаться следующей последовательности действий:

1) вычленить условие и требование задачи;

2) установить зависимость между данными и искомыми;

3) выявить способ составления уравнения и т. д.

;

7.6. Обобщающее повторение и их организация при обучении математике

Повторение с целью преподать забытое, показывает уже недостаток и вообще плохое преподавание в школе. В педагогической литературе существуют различные классификации повторения.

1. Повременному признаку

-в начале учебного года;

-повторение в течении учебного года;

-повторение после отдельных тем, или разделов учебного материала;

-повторение в конце учебного года.

2. По дидактическим целям

-аппаратное повторение;

-первично закрепляющее;

-подкрепляющее предупреждающее;

-корректирующее повторение;

-углубляющее;

-обобщающее и систематизирующее.

3. По частоте использования

-эпизодическое;

-периодическое;

-регулярное.

4. По характеру мыслительной деятельности учащихся

-активные; -пассивные.

5. По месту в процессе усвоения

-повторение, предшествующее изучению нового материала;

-повторение, сопутствующее изучению нового материала.

В связи с обобщающим повторением наиболее интенсивными являются «систематичность» и «системность». Систематичность – это качество знаний, которое характеризует наличие сознания ученика только содержательно логических связей между отдельными фрагментами знаний. Системность – это качество знаний,которое включает в себя глубину, обобщённость, осознанность, полноту и систематичность.

Цели обобщающего повторения:

-восстановить в памятиучащихся те знания, которые входят частично в содержание нового материала, а также провести сравнение сопоставление и установление логических связей ранее пройденного и нового материала;

-повторение следующее за изучением нового материала;

-закрепление полученных знаний, систематизация и обобщение их.

Обобщающее повторение на уровне теории.

Данное повторение призвано дать определённую трактовку изученным понятиям с позиции тех или иных фундаментальных идей рассмотренных в школьном курсе математики.

7.8. Методика изучения геометрических фигур и их измерений в курсе геометрии

На первых уроках изучения систематического курса геометрии закладываются основы курса планиметрии: вводятся основные понятия и свойства простейших геометрических фигур, позволяющие осуществить построение всего курса. Введение основных свойств геометрических фигур проводится на основе систематизации и обобщения знаний и представлений учащихся о геометрических фигурах, накопленных ими в процессе изучения математики. Изучение первых тем должно решить задачу введения терминологии, развития наглядных представлений и навыков изображения планиметрических фигур и простейших геометрических конфигураций, как по условию задачи, так и в ходе решения задач. Все это необходимо для дальнейшего изучения курса геометрии, в силу чего важными аспектами изучения систематического курса является работа с чертежами и рисунками, использование простейших геометрических инструментов (линейка, транспортир). При решении задач следует, прежде всего, опираться на наглядные представления учащихся. Тем не менее, решение задач следует использовать для постепенного формирования у учащихся первых навыков применения свойств геометрических фигур как опоры при решении задач. Для изучения фигур необходимо знать свойство отношений (параллельности, перпендикулярности, подобия). В истории преподавания геометрии всегда был актуален вопрос: с чего начинать изучение геометрии с линий или тел? На него в различные исторические периоды давались разные ответы, в советский и постсоветский период преобладала традиция начинать изучение геометрии с линий. Вторая традиция – раздельное изучение планиметрии и стереометрии.Давая рекомендации по изучению геометрических фигур, предполагается в определенной мере нарушить обе традиции, связано это с тем, что к началу изучения курса геометрии ученики знают почти все геометрические фигуры, за исключением может быть частных видов призм и частей шара. А так же с необходимостью развития пространственного мышления, включения субъективного опыта в процесс изучения геометрии, целесообразности изучения отношений параллельности, перпендикулярности на плоскости и в пространстве на фигурах. Изучение геометрических фигур и их измерений одним блоком позволяет значительно расширить тематику задачного материала, обеспечить более глубокую мотивацию за счет использования содержательных прикладных задач.

Введение понятия «геометрическая фигура».

Геометрия – это наука о свойствах геометрических фигур. Примерами геометрических фигур являются: треугольник, квадрат, окружность. (Рис.1)

Рис. 1.

7.10. Теорема, структура теоремы, виды теорем (примеры)

Структуру отдельных мыслей и способы их сочетаний называют формами мышления. С точки зрения формальной логики мышление характеризуется 3 основными формами: понятиями, суждениями, умозаключениями.

Пример понятия. Треугольник – это фигура, состоящая из 3 отрезков, попарно соединяющих 3 точки, не пересекающихся на одной прямой.

Пример суждения. Через любые две точки проходит прямая, и притом только одна.

Пример умозаключения. Если a>b, b>c, то a>c.

Математическое предложение, истинность которого устанавливается посредством доказательства – называется теоремой. Название «теорема» происходит от греческого слова τεορεμα – представление, зрелище. (т.к. в древности часто теоремы доказывались публично, на площадях, и они носили характер спора, дискуссии).

В школьном курсе математики для словесной формулировки теоремы используются три формы суждения:

1.Категорическая.

Пример.

Средняя линия трапеции параллельна основаниям и равна их полу сумме.

Постоянный множитель можно вынести за знак производной:

2.Условная.

Пример.

Если в треугольники два угла равны, то треугольник равнобедренный.

Еслина некотором промежутке, то на этом промежутке F(x)=c, с – постоянная.

3.Разделительная

Пример.

Плоскость и не лежащая на ней прямая либо не пересекается, либо пересекается в одной точке.

Теоремы категорической и разделительной формы можно переформулировать в терминах «если…, то…», т.е. обратить ее формулировку в условную.

Пусть, например, дана теорема:

«В ромбе диагонали взаимно-перпендикулярны». В условной форме формулировка этой теоремы будет выглядеть так: «Если четырёхугольник является ромбом, то его диагонали взаимно-перпендикулярны». Заметим, что разбор структуры теоремы более доступен для учащихся, ели онасформулирована в условной форме. Условная форма теоремы м.б. эффективно использована и для того, чтобы дать ответ на вопрос: «о свойстве или о признаке идет речь в теореме?». На этот вопрос легко ответить, если теорему сформулировать в условной форме. Если окажется, что рассматриваемое понятие находится в условие теоремы, то теорема выражает свойство этого понятия, если же понятие находится в заключение теоремы, то она выражает признак.

В школьном курсе математики формулируются и доказываются теоремы, имеющие различный вид: в одних теоремах из одного условия вытекает одно заключение, в других – из одного условия вытекает несколько заключений, в третьих – из нескольких условий вытекает одно заключение и т.д.

В любом случае теорема состоит из трех частей:

1.Разъяснительная часть, в которой описывается множество М объектов, о которых идет речь в этой теореме.

2.Условие теоремы, то есть некоторый предикат А(х), заданный на множестве М.

3.Заключение теоремы – некоторый предикат В(х), заданный на том же множестве М.

В символах математической логики теорема м.б. записана следующим образом:

Часто в литературе используется такая терминология:

Тезис – доказываемое утверждение. Аргументы (основание доказательства)- используемые в доказательстве уже известные утверждения, из которых необходимо следует истинность доказываемого тезиса. Демонстрация – последовательность расположения аргументов и выводов, образующих цепь умозаключений. При доказательстве тезис должен удовлетворять следующим требованиям: быть ясным и точно определенным; оставаться тождественным, т.е. одним и тем же на протяжении всего доказательства; не должен содержать в себе логического противоречия; не должен находиться в логическом противоречии с суждениями по данному вопросу, высказанными ранее. Требования к аргументам доказательства таковы: они должны быть истинным предложением данной теории; быть достаточным основанием для доказываемого предложения; истинность которого доказана самостоятельно, независимо от доказываемого предложения.

С любой теоремой связаны еще три теоремы.

Четыре вида теорем:

1.– прямая теорема.

2.– обратная теорема.

3.– противоположная теорема.

4.– обратная к противоположной теорема (контрапозитивная).

Пример:

1.Если 4 – угольник параллелограмм, то диагонали его, пересекаясь, делятся пополам (истинно).

2.Если в 4 - угольнике диагонали пересекаясь, делятся пополам, то этот 4 – угольник – параллелограмм (истинно).

3.Если 4 – угольник не параллелограмм, то его диагонали, пересекаясь, не делятся пополам (истинно).

4.Если в 4 – угольнике диагонали пересекаясь, не делятся пополам, то такой 4 – угольник не параллелограмм (истинно).

7.11. Формы организации изучения новой темы на уроках математики

Уроки математики обладают рядом отличительных особенностей, которые необходимо учитывать при конструировании современного урока математики.

• содержание опирается на ранее изученное, подготавливая базу для усвоения новых знаний;

• уделяется большое внимание развитию у учащихся логического мышления, умений рассуждать и доказывать;

• необходимо создавать условия для того, чтобы каждый ученик мог усвоить на уроке самое главное в изучаемом материале;

• математика служит опорным предметом для изучения смежных дисциплин;

• теоретический материал осознается и усваивается в процессе решения задач.

Конструирование урока можно осуществить по следующему алгоритму:

1. Постановка задачи на использование информационных технологий на уроке

2. Определение информации, обеспечивающей решение учебных задач посредством информационных технологий

3. Выбор средств информационных технологий, адекватных поставленным задачам

4. Разработка методики использования информационных технологий в процессе решения задач

5.Совершенствование традиционных методик обучения при использовании ИКТ.

7.12. Методика изучения многогранников и их объемов в школьном курсе математики

Само определение понятия многогранника оказывается как раз таким вопросом, где необходимо особенно внимательно сочетать наглядные представления, рассмотрение реальных примеров и логической точности формулировок. Формулировки должны исходить из реальных примеров, из наглядных представлений и возвращаться к ним для проверки и дальше - для применения.

Выделяют два основных способа введения понятия многогранника в школьном курсе стереометрии:

1. многогранник как поверхность;

2. многогранник как тело.

Чаще используется второй путь.

Дать строгое определение понятию многогранника в школе трудно, так как в определение входят такие понятия как поверхность, ограниченность, внутренние точки и др. Такая попытка была сделана в книге В.М. Клопского, З.А. Скопеца, М.И. Ягодовского «Геометрия 9-10» [16], но было очень сложно, так как определение вводилось в несколько шагов, было много вспомогательных понятий.

Наиболее целесообразно дать описание на основе наглядных представлений школьника. Проще и короче всего определить многогранник как тело, поверхность которого состоит из многоугольников (в конечном числе). При этом «тело» и «поверхность» можно понимать в наглядном смысле, как понимают обычно. Тело в отвлечении его от материальности – это часть пространства. Поэтому данное определение можно пересказать и так:многогранник – это часть пространства, ограниченная конечным числом многоугольников.

Виды и роль наглядных средств при изучении многогранников

Тема «Многогранники», как никакая другая тема школьного курса стереометрии, за исключением, быть может, изучения круглых тел, дает широкие возможности использования различных наглядных средств. Наглядность является обязательным качеством любого обучения. Путем целенаправленных действий мы формируем в сознании учащегося некоторую систему понятий, отношений между ними. Для того чтобы обучение было успешным, необходимо, чтобы ученик мог воспринимать эту систему и работать с ней. Но для этого необходимо предъявить ученику некоторую ее материальную модель. Для этого применяют наглядные средства обучения. Например, если изучается понятие пирамиды, то такой моделью может быть: 1) словесное описание (определение) этого понятия;