
госы / Шпоры - 1
.docx|
1.1 Группы: понятие, примеры. Подгруппа. Критерий подгруппы Всюду в дальнейшем запись (G, ) означает, что на непустом множестве G задана алгебраическая операция “”.Определение. Множество (G, ) называется группой, если выполнены следующие условия: (1) операция “” ассоциативна, т.е. (x, y, zG) (xy)z = x(yz); (2) множество G обладает нейтральным элементом относительно операции, т.е.(eG)(xG) xe = ex = x; (3) каждый элемент множества G обладает симметричным элементом, т.е. (xG) (yG) xy = yx = e.Примеры групп.Примеры групп весьма разнообразны. Перечислим некоторые из них.Числовые группы(группы, элементы которых являются комплексными числами).а) Аддитивные группы целых чисел Z, рациональных чисел Q, действительных чиселR, комплексных чисел C.б) Мультипликативные группы ненулевых рациональных чисел Q*, ненулевых действительных чисел R*, ненулевых комплексных чисел C*, положительных рациональных чисел Q+, положительных действительных чисел R+.Группы подстановокSn, действующих на множестве {1, 2,...,n}. Матричные группы. Укажем на две важнейшие матричные группы:GLn(R) – полная линейная группа (группа обратимых матриц),SLn(R) – специальная линейная группа (группа матриц с единичным определителем).Определение. Если подмножество Н группы само является группой относительно умножения группы G, то говорят, что Н – подгруппа группы G.Пример.Мультипликативная группа полож-ных рацион-х чисел явл. подгруппой группы , группа - подгруппа . Пример. Рассмотрим группы и . Множество рациональных чисел, отличных от нуля, Q0является подмножеством всех рациональных чисел Q. Однако, сказать, что Q0 подгруппа Qнельзя, т.к. операции, рассматриваемые на них, различны. Каждая группа имеет, по меньшей мере, две подгруппы: сама Gи единичная подгруппа . Они называются тривиальными подгруппами G.Подгруппы, отличные от тривиальных подгрупп называютсясобственными подгруппами. Для того чтобы установить, что непустое подмножество Н группы G есть подгруппа этой группы, достаточно проверить два условия: |
1.2. Матрицы и операции над ними. Обратная матрица и ее нахождение Определение.Суммой
матриц
А и В одинаковой размерности mn
называется матрица С той же размерности,
каждый элемент которой равен сумме
элементов матриц А и В, стоящих на тех
же местах:
Свойства сложения:
Замечание. Справедливость этих свойств следует из определения операции сложения матриц. Определение. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число. Свойства умножения матрицы на число:
Определение.Произведением
матрицы А размерности mp
и матрицы Вразмерности Замечание.
Операция перемножения матриц
некоммутативна, т.е.
Для квадратных матриц одного порядка произведения АВ и ВА существуют и имеют одинаковую размерность, но их соответствующие элементы в общем случае не равны. Однако в некоторых случаях произведения АВ и ВА совпадают. Определение.
Квадратная
матрица А называется вырожденной,
если
|
Определение.
Квадратная матрица В называется
обратной
к квадратной матрице А того же порядка,
если АВ
= ВА = Е.
При этом В обозначается
Теорема. Для существования обратной матрицы необходимо и достаточно, чтобыисходная матрица была невырожденной. Доказательство.
Тогда
любой элемент произведения
Теорема доказана. Пример. Найдем
матрицу, обратную к
|
1.5.Делимость в кольце целых чисел Определение. Пусть a, b принад. Z.Число а делится на число b0, если найдется такое число q принад. Z, что а = qb. Синонимы: а кратно b; b — делитель а. Теорема (о делении с остатком).Для данного целого отличного от нуля числа b, всякое целое число а единственным образом представимо в виде а = bq+ r, где 0r<| b |(1). Доказательство существования.Пусть bq – наибольшее кратное числа b, не превосходящее а (см. рис. ). ( a = 3b+r)
Тогда bqа< b(q+1)и0 а- bq< b. Полагая а- bq= r, получаем представление(1). Доказательство единственности.Пусть а=bq+r и а=bq1+ r1 — два таких представления. Значит 0=а–а=b(q–q1)+(r–r1).Здесь 0делится на b; b(q–q1) делится на b, следовательно (r–r1) обязано делиться на b. Так как 0<=r<b и 0<=r1 <b, то r–r1<b и r–r1 делится на b, значит r–r1 равно нулю, а, значит и q—q1 равно нулю, т.е. два таких представления совпадают. Замечание. Число q называется неполным частным, а число r — остатком от деления а на b. Заметим, что остаток — всегда есть число неотрицательное, а вот неполное частное может быть каким угодно целым числом. Алгоритм Евклида Пусть a>b; a, b принад. Z. a=bq1+r1,0<=r1<b, b=r1q2+r2,0<=r2<r1, r1=r2q3+r3,0<=r3<r2 r2 = r3 q4+r4, 0<=r4<r3, …………………….. rn-3=rn-2qn-1+rn-1,0<=rn-1<rn-2. rn-2=rn-1qn+rn, 0<=rn<rn-1 rn-1= rnqn+1,r n +1 = 0 Имеем: b >r1 >r2 >... >rn> 0, следовательно, процесс оборвется максимум через b шагов. Покажем, что rn=(a, b). Просмотрим последовательно равенства сверху вниз: всякий делитель а и b делит r1,r2,..., rn. Если же просматривать эту цепочку равенств от последнего к первому, то видно, чтоr n -1r n, r n -2 r n, и т.д., т.е. r n делит а и b. Поэтому r n - наибольший общий делитель чисел а и b. Замечание. Алгоритм Евклида дает практический способ нахождения чисел u и v из Z таких, что rn= au + bv = ( a, b ). Действительно, из цепочки равенств имеем: r n = r n -2 - r n -1 q n = r n -2 - ( r n -3 - r n -2 q n -1 ) q n =... (идем по цепочке равенств снизу вверх, выражая из каждого следующего равенства остаток и подставляя его в получившееся уже к этому моменту выражение) ... = au + bv= ( a,b ). |
|
1.3. Решение и исследование систем линейных уравнений Определение.Системой линейных уравнений (линейной системой) называется система вида
где Определение.Решением
линейной системы называется набор
чисел Определение. Линейная система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Определение. Совместная линейная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Определение. Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот. Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы. Элементарное преобразование 1. Если какое-либо уравнение системы умножить на некоторое отличное от нуля число, а остальные уравнения оставить без изменения, то получится система, равносильная данной. Элементарное преобразование 2. Если к какому-либо уравнению системы прибавить другое, а все остальные уравнения оставить без изменения, то получится система, равносильная данной. Элементарное преобразование 3. Если к какому-либо уравнению прибавить другое, умноженное на некоторое число, а все остальные уравнения оставить без изменения, то получится система, равносильная данной. Назовем расширенной матрицей системы (1) матрицу вида
|
Теорема (теорема Кронекера-Капелли). Система (1) совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы. Формулы Крамера. Пусть дана система n линейных уравнений с n неизвестными
или в матричной форме А*Х=В (3). Основная матрица А такой системы квадратная. Определитель этой матрицы
называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной. Умножив обе части уравнения (3) слева на матрицу A-1, получим A-1*A*X=A-1*B Поскольку. A-1*A=Eи Е*Х=Х, то X=A-1*B(4). Отыскание решения системы по формуле (4) называют матричным способом решения системы. Матричное равенство (4) запишем в виде то есть
|
1.4 Сравнения в кольце целых чисел. Полная и проведенная системы вычетов. Теоремы Эйлера и Ферма Определение.Целые числаaиb сравнимы по модулюm (m – натуральное), еслиa-b делится наm.Запись этого факта выглядит так:a b(modm).Свойства сравнений. Свойство 1.Отношение сравнимости рефлексивно, симметрично, транзитивно. Замечание. По свойству 1 отношение сравнимости являетсяотношением эквивалентности. Это отношение делит множество целых чисел на непересекающиеся классы эквивалентных межу собой элементов. В один класс входят равноостаточные числа. Свойство 2. Сравнения по одинаковому модулю можно почленно складывать. Доказательство.Пустьa1b1(modm),a2b2(modm).Это означает, что a1 =b1 +mt1,a2 =b2 +mt2.Послесложенияпоследних двух равенств получим a1 +a2 =b1 +b2 +m(t1 +t2), что означает a1+a2b1+b2 (modm). Свойство
3. Слагаемое,
стоящее в какой-либо части сравнения,
можно переносить в другую часть,
изменив его знак на противоположный.
Доказательство. Свойство
4. К
любой части сравнения можно прибавить
любое число, кратное модулю.
Доказательство. Свойство
5. Сравненияпоодинаковомумодулюможно
почленно перемножать. Доказательство. Свойство 6. Обе части сравнения можно разделить на их общий делитель, взаимно простой с модулем. Доказательство.Пустьab(modm),a=a1d,b=b1d.Тогда (a1 -b1)d делится на m. Поскольку d и m взаимно просты, то на m делится именно (a1 -b1), что означает a1b1 (modm). Свойство 7. Обе части сравнения и его модуль можно умножить на одно и то же целое число или разделить на их общий делитель. Определение.Классом элемента а по модулюm называется множество всех целых чисел х сравнимых с а по модулю m. Обозначение.или [a]modm. Теорема.Число классов по модулюmконечно и равноm. Доказательство. Разделимцелоечислоана натуральное mс остатком, т.е. a=mq+r, 0 r<m, a-r=mq, ar(modm) |
Следовательно, а. Остатками при делении на mявляются числа 0, 1, 2, …, m-1, т.е. число различных остатков, а значит, ичисло различных классов равно m. Определение. Совокупность вычетов, взятых по одному из каждого класса, называется полной системой вычетов (ПСВ) по модулю m (в полной системе вычетов, таким образом, всего m штук чисел). Пример: Пусть m = 5. Тогда: 0, 1, 2, 3, 4 - наименьшие неотрицательные вычеты (ПСВ); -2, -1, 0, 1, 2 - абсолютно наименьшие вычеты (ПСВ). Теорема. 1) Любые m штук попарно несравнимых по модулю m чисел образуют полную систему вычетов по модулю m. 2) Если а и m взаимно просты, а x пробегает полную систему вычетов по модулю m, то значения линейной формы аx+b, где b - любое целое число, тоже пробегают полную систему вычетов по модулю m. Доказательство.1) Количество различных классов вычетов по модулю m равно m.Поэтому полная система вычетов содержит m элементов. Числа различных классов вычетов попарно несравнимы по модулю (по критерию равенства классов). Отсюда следует справедливость первого утверждения. Докажем утверждение 2). Чисел аx+bровно m штук. Покажем, что они междусобойне сравнимы по модулю m. Пусть для некоторых различных x1 и x2 из полной системы вычетов оказалось, что ax1+b ax2 +b(modm).Тогда, по свойствам сравнений получаем: ax1ax2 (modm), x1 x2 (modm) – противоречие с тем, что x 1 и x 2 различны и взяты из полной системы вычетов. Определение. Приведенной системой вычетов (ПрСВ) по модулю m называется совокупность всех вычетов взятых по одному из каждого обратимого класса вычетов. Определение. Класс вычетовпомодулюmназывается обратимым, если существует другой класс вычетов по модулю m, такой что=. Приведенная система вычетов по модулю m содержит (m) штук вычетов, где (m)– функция Эйлера – число чисел, меньших m и взаимно простых с m. Теорема. Для того чтобы класс вычетовпо модулюmбыл обратим, необходимо и достаточно, чтобы он состоял из чисел взаимно простых с модулем. Пример. Пусть m = 42. Тогда ПрСВ: 1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41. Теорема. 1) Любые(m) чисел, попарно не сравнимые по модулю m и взаимно простые с модулем, образуют приведенную систему вычетов по модулю m. 2) Если (a,m ) = 1 и x пробегает приведенную систему вычетов по модулю m, то аxтак же пробегает приведенную систему вычетов по модулю m.). Из всего этого следует справедливость первого утверждения. |
|
1.6. Определители, их свойства и методы вычислений Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.
Определение.Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
Определение. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
Основные свойства определителей. Сформулируем и докажем основные свойства определителей 2-го и 3-го порядка (доказательство проведем для определителей 3-го порядка).
Свойство 1. Определитель не изменяется при транспонировании, т.е.
Доказательство .
|
же свойствами будут обладать и столбцы. Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.
Доказательство.
Свойство 4. Определитель, имеющий две равные строки, равен 0.
|
2. Геометрия 2.1. Базис векторного пространства. Скалярноепроизведение векторов
Базисом
векторного
пространства называется такая система
векторов, которая: 1) задана в определенном
порядке; 2) линейно независима; 3)
любой вектор пространства Vявляется
линейной комбинацией данной
системы векторов. Теорема.
Любая система трех некомпланарных
векторов, взятых в
определенном порядке, является базисом
векторного пространства V(без
доказательства). Теорема.
Любой базис пространства Vсостоит
из трех векторов (без доказательства).
Замечание.
Число
векторов базиса называется размерностью
векторного
пространства. Из теоремы 2 следует,
что размерность Vравна
3:
Замечание.
Если
рассматривать
|
Свойства координат векторов:
1)
если даны координаты векторов
Следствие 2.Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Следствие 3. При умножении вектора на число каждая его координата умножается на то же число.
2)
Базис
1)
2)
углы
Пусть
в ОНБ
Скалярным
произведением этих
векторов называется
число
При Если
в ортонормированном базисе вектор
|

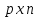 называется матрица Сразмерности
называется матрица Сразмерности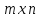 ,
каждый элемент которой
,
каждый элемент которой
 определяется формулой:
определяется формулой: